
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение дифференциального уравненияСодержание книги
Поиск на нашем сайте Общим решением неоднородного дифференциального уравнения является сумма, состоящая из общего решения однородного уравнения ус и частного решения неоднородного уравнения уb, т.е.
Общее решение однородного уравнения порядка n ищут в виде:
где p 1, p 2 … pn — корни соответствующего ему характеристического уравнения.
Частное решение неоднородного уравнения в общем случае ищется с учетом вида правой части. При исследовании звеньев САР частное решение неоднородного уравнения обычно ищу для случая, когда приложенное скачкообразное внешнее воздействие (см. рис. 21) сохраняется постоянным во времени, т.е.
Постоянные интегрирования С 1, С 2 … Сn определяют из начальных условий, которые можно принять нулевыми т.е. при t = 0,
Применим изложенную методику к решению уравнения объекта (13). Соответствующее уравнению (20)характеристическое уравнение Тогда
Частное решение неоднородного уравнения ищем в виде:
подставляя значения
и, следовательно,
Исходя из нулевых начальных условий, т.е. при t = 0 y = 0, получим В окончательном виде решение уравнения (13) или его переходная функция будет:
Графически переходной процесс, соответствующий переходной функции (26), будет иметь вид экспоненты, изображенной на рис. 22.
Рис. 22. График переходного процесса
Коэффициент усиления k показывает зависимость выходной координаты от входной при различных установившихся режимах. Постоянная времени Т 0характеризует скорость изменения регулируемой величины в переходном процессе. Для экспоненциальной функции такого вида Т 0будет являться проекцией касательной, проведенной в любой точке экспоненты на линию установившегося значения Теоретически переходный процесс продолжается бесконечно долго. В практических инженерных расчетах принимают, что переходный процесс закончится, когда регулируемая величина достигнет значения:
Подставляя это значение в выражение (26), можем определить продолжительность переходного процесса в зависимости от величины п:
В практических расчетах принимают п = (0,99÷0,95). Для этих значений продолжительность переходного процесса соответственно будет:
Автоматические регуляторы Автоматический регулятор формирует закон регулирования и обеспечивает заданные динамические свойства САР. Автоматические регуляторы разделяются на регуляторы прямого и непрямого действия. В регуляторах непрямого действия перемещение регулирующего органа осуществляется за счет энергии постороннего источника, в зависимости от вида которой различают электрические, пневматические, гидравлические и комбинированные регуляторы. В общем случае регулятор можно отнести к колебательному звену, динамика которого описывается уравнением 2-го порядка [см. уравнение (50)]. Однако в связи с тем, что постоянные времени Т 1и Т 2 в уравнении (50) обычно во много раз меньше постоянной времени объекта Т 0, в практических расчетах ими часто пренебрегают и считают регулятор идеальным звеном [см. уравнение (29)]. В зависимости от характеристики действия регуляторы делятся: на статические или пропорциональные (П-регуляторы), в которых регулирующее воздействие пропорционально отклонению регулируемой величины; уравнение динамики идеального статического регулятора имеет вид:
на астатические или интегральные (И-регуляторы), у которых регулирующее воздействие пропорционально интегралу отклонения регулируемой величины; уравнение динамики идеального астатического регулятора имеет вид:
на изодромные или пропорционально-интегральные (ПИ-регуляторы), у которых регулирующее воздействие пропорционально отклонению и интегралу отклонения регулируемой величины; уравнение динамики идеального изодромного регулятора имеет вид:
на регуляторы с воздействием по производной (или ПД-регуляторы), у которых регулирующее воздействие пропорционально отклонению и производной отклонения регулируемой величины. Применяются также регуляторы, у которых регулирующее воздействие пропорционально отклонению, производной и интегралу отклонения регулируемой величины — изодромные с воздействием по производной (ПИД-регуляторы); уравнение динамики ПИД-регулятора имеет вид:
|
||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 249; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.011 с.) |

 . (21)
. (21) , (22)
, (22) . (23)
. (23) и т. д. (24)
и т. д. (24) будет иметь один корень
будет иметь один корень  .
. . (25)
. (25)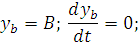
 и
и  в уравнение (13), получим:
в уравнение (13), получим:
 .
. или
или  .
. . (26)
. (26)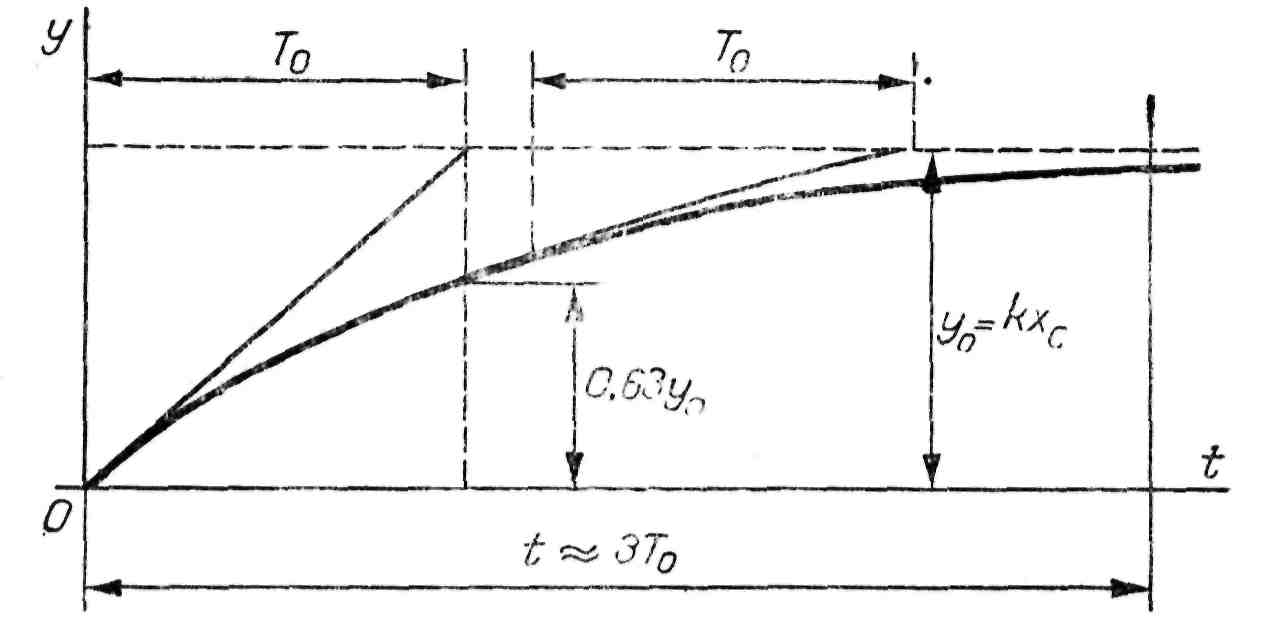
 .
. . (27)
. (27) . (28)
. (28) = 4,6 Т 0 и
= 4,6 Т 0 и  ; (29)
; (29) ; (30)
; (30) ; (31)
; (31) . (32)
. (32)


