
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Text 7. The Idea of the Energy-Momentum MethodСодержание книги
Поиск на нашем сайте
The setting of the energy-momentum method is that of a mechanical system with symmetry with a configuration space Q and phase space T* Q and a symmetry group G acting, with a standard momentum map J: T*Q → g *, where g * is the Lie algebra of G. Of course, one gets the Lie–Poisson case when Q = G. The rough idea for the energy momentum method is first to formulate the problem directly on the unreduced space. Here, relative equilibria associated with a Lie algebra element ξ are critical points of the augmented Hamiltonian The surprising thing is that the second variation of Hξ at the relative equilibrium can be arranged to be block diagonal, using splittings that are based on the mechanical connection, while at the same time, the symplectic structure also has a simple block structure, so that the linearized equations are put into a useful canonical form. Even in the Lie–Poisson setting, this leads to situations in which one gets much simpler second variations. This block diagonal structure is what gives the method its computational power. The general theory for carrying out this procedure was developed in Simo, Posbergh, and Marsden [1990, 1991] and Simo, Lewis, and Marsden [1991]. An exposition of the method may be found, along with additional references, in Marsden [1992]. It is of interest to extend this to the singular case, which is the subject of ongoing work; see Ortega and Ratiu [1997, 1998] and references therein. The energy-momentum method may also be usefully formulated in the Lagrangian setting, which is very convenient for the calculations in many examples. The general theory for this was developed in Lewis [1992] and Wang and Krishnaprasad [1992]. This Lagrangian setting is closely related to the general theory of Lagrangian reduction. In this context one reduces variational principles rather than symplectic and Poisson structures, and for the case of reducing the tangent bundle of a Lie group, this leads to the Euler–Poincaré equations rather than the Lie–Poisson equations.
Слова к тексту
Letters and Sounds
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 349; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.005 с.) |

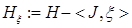 . The idea is now to compute the second variation of Hξ at a relative equilibrium ze with momentum value μe subject to the constraint J = μe and on a space transverse to the action of G μ e, the subgroup of G that leaves μe fixed. Although the augmented Hamiltonian plays the role of H + C in the Arnold method, notice that Casimir functions are not required to carry out the calculations.
. The idea is now to compute the second variation of Hξ at a relative equilibrium ze with momentum value μe subject to the constraint J = μe and on a space transverse to the action of G μ e, the subgroup of G that leaves μe fixed. Although the augmented Hamiltonian plays the role of H + C in the Arnold method, notice that Casimir functions are not required to carry out the calculations.


