
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Text 7. Some History of the Momentum Map
The momentum map can be found in the second volume of Lie [1890], where it appears in the context of homogeneous canonical transformations, in which case its expression is given as the contraction of the canonical one-form with the infinitesimal generator of the action. On page 300 it is shown that the momentum map is canonical and on page 329 that it is equivariant with respect to some linear action whose generators are identified on page 331. On page 338 it is proved that if the momentum map has constant rank (a hypothesis that seems to be implicit in all of Lie's work in this area), its image is Ad*-invariant, and on page 343, actions are classified by Ad*-invariant submanifolds. We now present the modern history of the momentum map based on information and references provided to us by B. Kostant and J.-M. Souriau. We would like to thank them for all their help. In Kostant’s 1965 Phillips lectures at Haverford (the notes of which were written by Dale Husemoller), and in the 1965 U.S. – Japan Seminar (see Kostant [1966]), Kostant introduced the momentum map to generalize a theorem of Wang and thereby classified all homogeneous symplectic manifolds; this is called today "Kostant's coadjoint orbit covering theorem." These lectures also contained the key points of geometric quantization. Souriau introduced the momentum map in his 1965 Marseille lecture notes and put it in print in Souriau [1966]. The momentum map finally got its formal definition and its name, based on its physical interpretation, in Souriau [1967]. Souriau also studied its properties of equivariance, and formulated the coadjoint orbit theorem. The momentum map appeared as a key tool in Kostant's quantization lectures (see, e.g., Theorem 5.4.1 in Kostant [1970]), and Souriau [1970] discussed it at length in his book. Kostant and Souriau realized its importance for linear representations, a fact apparently not foreseen by Lie (Weinstein [1983a]). Independently, work on the momentum map and the coadjoint orbit covering theorem was done by A. Kirillov. This is described in Kirillov [1976b]. This book was first published in 1972 and states that his work on the classification theorem was done about five years earlier (page 301). The modem formulation of the momentum map was developed in the context of classical mechanics in the work of Smale [1970], who applied it extensively in his topological program for the planar n -body problem. Marsden and Weinstein [1974] and other authors quickly seized on the treasures of these ideas. Ask 5-6 questions on the text. What are the key words of the text? Give a short summary of the text using the key words. Text 8. Routh Reduction An abelian version of Lagrangian reduction was known to Routh by around 1860. A modern account was given in Arnold [1988] and, motivated by that, Marsden and Scheurle [1993a] gave a geometrization and a generalization of the Routh procedure to the nonabelian case. In this section we give an elementary classical description in preparation for more sophisticated reduction procedures, such as Euler–Poincare reduction in Chapter 13. We assume that Q is a product of a manifold S and a number, say k, of copies of the circle As we shall see after Chapter 9 is studied, invariance of L under the action of the abelian group A basic class of examples (for which Exercises 8.9-1 and 8.9-2 provide specific instances) are those for which the Lagrangian L has the form kinetic minus potential energy:
where there is a sum over Because
are conserved quantities. In the case of the Lagrangian (8.9.1), these momenta are given by
|
|||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 353; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.36.141 (0.007 с.) |
 , namely
, namely  . The factor S, called shape space, has coordinates denoted
. The factor S, called shape space, has coordinates denoted  and coordinates on the other factors are written
and coordinates on the other factors are written  . Some or all of the factors of
. Some or all of the factors of  , a = 1, …, k are cyclic, that is, they do not appear explicitly in the Lagrangian, although their velocities do.
, a = 1, …, k are cyclic, that is, they do not appear explicitly in the Lagrangian, although their velocities do. is another way to express that fact that
is another way to express that fact that  (8.9.1)
(8.9.1)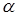 ,
,  from 1 to m and over a, b from 1 to k. Even in simple examples, such as the double spherical pendulum or the simple pendulum on a cart (Exercise 8.9-2), the matrices
from 1 to m and over a, b from 1 to k. Even in simple examples, such as the double spherical pendulum or the simple pendulum on a cart (Exercise 8.9-2), the matrices  can depend on x.
can depend on x.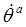 are cyclic, the corresponding conjugate momenta
are cyclic, the corresponding conjugate momenta (8.9.2)
(8.9.2)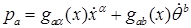 .
.


