
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Осевая игра (осевые зазоры) подшипников каченияСодержание книги
Поиск на нашем сайте
Валы редукторов обычно монтируют на подшипниках качения. Нормальная работа последних зависит от свободы взаимного перемещения колец и тел качения, которая определяется наличием в подшипниках радиальных зазоров между дорожками и телами качения. Следствием наличия радиального зазора в подшипнике является его осевая игра. Осевой игрой называют величину полного осевого перемещения кольца подшипника из одного крайнего положения в другое при неподвижном другом кольце. Величина осевой игры подшипников зависит от конструкции подшипников, способа их установки на валу, наличия радиального зазора между дорожками и телами качения и характеризуется осевым смещением вала. Осевая игра подшипников обычно обеспечивается за счет регулировочных прокладок, помещаемых между крышкой подшипника и корпусом редуктора или другими конструктивными способами. Величину осевой игры для конических однорядных роликовых подшипников можно определить по таблице 8.4 [4, 37], а для радиально-упорных однорядных шариковых подшипников по таблице 8.5 [4,37]. Таблица 8.4
Таблица 8.5
Величину осевой игры для радиальных однорядных шариковых подшипников находят по номограмме рисунок 8.6, предварительно определив минимальный и максимальный радиальные зазоры в подшипнике по таблице 8.6. Таблица 8.6 - Радиальные зазоры в подшипниках [4]
Пример. У подшипника 306 необходимо определить допустимые значения осевой игры. Решение. По таблице 8.6 устанавливаем, что такой подшипник может теоретически иметь радиальные зазоры g r min =10 мкм и g r max =24 мкм. По номограмме рисунка 8.6 определяем величину 2S/gr. Для gr min = 10 мкм находим 2S/gr = 12, тогда осевая игра 2S = 12·0,01 = 0,12 мм. Для gr max=24 мкм находим 2S/gr = 8. Тогда осевая игра 2S = 8·0,024 = 0,192 мм. Таким образом, для подшипника 306 осевая игра может теоретически изменяться от 0,12 до 0,192 мм. Размерные цепи Собранные из отдельных деталей машина или механизм, будут нормально работать только в том случае, если каждая деталь изготовлена с заданной точностью и правильно занимает предназначенное для нее место среди других деталей, выполняя свои функции. Необходимое положение поверхностей деталей и их осей относительно других деталей в собранном изделии обеспечивается расчетом размерных цепей. Размерная цепь - это совокупность взаимосвязанных размеров, образующих замкнутый контур и непосредственно участвующих в решении поставленной задачи. Размерные цепи могут быть: конструкторские, технологические, измерительные. Конструкторская размерная цепь составляется для решения задачи по обеспечению точности при конструировании изделия, технологическая - для решения задачи по обеспечению точности при изготовлении, а измерительная при измерении величин, характеризующих точность изделия. Основой для составления и расчета линейных и угловых размерных цепей является РД 50-635-87 [33]. Все размеры, входящие в размерную цепь называют звеньями и обозначают одной прописной буквой русского алфавита с соответствующим индексом. Звенья размерной цепи разделяют на составляющие и замыкающее. Замыкающее звено может быть только одно. Это звено, которое получается последним в результате решения поставленной задачи при изготовлении детали или сборки сборочной единицы, а также при измерении. Составляющих звеньев может быть различное количество, определяемое назначением изделия и решением поставленной задачи. На рисунке 9.1 приведены примеры простейших трехзвенных размерных цепей, где А1 и А2 - составляющие звенья; АΔ - замыкающее звено. Составляющие звенья по разному влияют на замыкающее звено. В зависимости от этого влияния их разделяют на увеличивающие и уменьшающие. Увеличивающими называют такие звенья, с увеличением размеров которых замыкающее звено увеличивается, а уменьшающими такие, с увеличением которых замыкающее звено уменьшается. На рисунке 9.1 звено A1 - увеличивающее, А2 - уменьшающее. В более сложных размерных цепях удобно использовать правило обхода по замкнутому контуру [34]. С этой целью замыкающему звену дают произвольное направление стрелкой, поставленной над обозначением звена (рисунок 9.2) и обходят все звенья, начиная с замыкающего так, чтобы образовался замкнутый поток направлений. Тогда все звенья, имеющие направление стрелок на схеме размерной цепи одинаковое с замыкающим будут уменьшающими, а все остальные - увеличивающими. Если замыкающему звену задавать всегда направление только налево, то тогда при обходе по замкнутому контуру все составляющие звенья, имеющие направление стрелок налево будут уменьшающими, а с направлением стрелок направо - увеличивающими. Этот частный случай общего правила обхода по замкнутому контуру часто используется [33, 36, 44]. В зависимости от взаимного расположения звеньев размерные цепи разделяют на линейные (с параллельными звеньями), плоские и пространственные. Все размерные цепи рассчитывают по формулам для линейных цепей. Пространственные размерные цепи приводят к плоским, а плоские к линейным путем проектирования размеров цепи на одно направление, в качестве которого обычно используют направление замыкающего звена. Расчет размерных цепей является обязательным этапом при конструировании машин. Он способствует обеспечению взаимозаменяемости, повышению качества изделия и снижению трудоемкости изготовления. Расчет размерных цепей заключается в нахождении допусков и предельных отклонений всех звеньев цепи исходя из требований конструкции и технологии изготовления.
При решении размерных цепей различают две задачи: ü Необходимо определить номинальный размер, допуск и предельные отклонения замыкающего звена по известным номинальным размерам и предельным отклонениям оставляющих звеньев. Эту задачу называют обратной и часто применяют для проверочных расчетов. Она имеет однозначное и достаточно простое решение. ü Необходимо определить допуск и предельные отклонения всех составляющих звеньев по известным номинальным размерам звеньев, допуску и предельным отклонениям замыкающего звена. Эту задачу называют прямой. Она достаточно сложна и имеет несколько решений. Размерные цепи могут решаться методами дающими различные результаты. Так, в РД 50-635-87 [33] предусмотрены следующие методы: полной взаимозаменяемости (на максимум - минимум); неполной взаимозаменяемости (с использованием положений теории вероятностей); групповой взаимозаменяемости; метод пригонки; метод регулирования. Принятые обозначения [33]: А1 А2;... Aj - обозначение и номинальный размер звеньев размерной цепи А; АΔ - обозначение и номинальный размер замыкающего звена размерной цепи А;
- компенсирующее j-e составляющее звено размерной цепи А; n - количество увеличивающих звеньев; р - количество уменьшающих звеньев; m - 1 - общее количество составляющих звеньев: n + р = m - 1; m - количество звеньев размерной цепи; ЕSАΔ - верхнее предельное отклонение замыкающего звена размерной цепи А; Е i АΔ - нижнее предельное отклонение замыкающего звена размерной цепи А; ЕSA j - верхнее предельное отклонение составляющего звена размерной цепи А; E i A j - нижнее предельное отклонение составляющего звена размерной цепи А; ТАΔ - допуск замыкающего звена размерной цепи А; TA j - допуск j-ro звена размерной цепи А; ЕсАΔ - координата середины поля допуска замыкающего звена размерной цепи А; EcA j - координата середины поля допуска j-ro составляющего звена размерной цепи А; ЕСVАΔ - координата середины поля рассеяния замыкающего звена размерной цепи А; EcvAj - координата середины поля рассеяния j-ro составляющего звена размерной цепи А; ЕmАΔ - координата центра группирования замыкающего звена размерной цепи А; EmAj - координата центра группирования j-ro составляющего звена размерной цепи А; Vk - величина компенсации; λ - относительное среднее квадратическое отклонение; tΔ - коэффициент риска; α - коэффициент относительной асимметрии; ξA j - передаточное отношение j-ro звена размерной цепи А; N - число ступеней размеров неподвижного компенсатора; р - процент риска. Основные расчетные формулы [33] Номинальный размер замыкающего звена размерной цепи А определяют по формуле:
где j =1,2,... m - порядковый номер звена размерной цепи; ξA j - передаточное отношение j-ro звена размерной цепи А. В зависимости от вида размерной цепи передаточное отношение может иметь различное содержание и значение. Так, например, для линейных размерных цепей (цепей с параллельными звеньями) передаточные отношения равны: ξ j = 1 для увеличивающих составляющих звеньев; ξ j = -1 и для уменьшающих составляющих звеньев. По этой причине для линейных размерных цепей зависимость (9.1) записывают в виде [44]:
где n - количество увеличивающих звеньев; р - количество уменьшающих звеньев. Допуск замыкающего звена ТАΔ при расчете на максимум - минимум:
Координата середины поля допуска ЕсАΔ замыкающего звена размерной цепи А:
Предельные отклонения замыкающего звена АΔ:
Возможно определение предельных отклонений замыкающего звена по зависимостям [44]:
Предельные размеры замыкающего звена:
При расчете вероятностным методом допуск замыкающего звена:
где t∆ - коэффициент риска, принимаемый из таблицы 9.1. Таблица 9.1 - Коэффициент риска [33]
Для размерных цепей с параллельными звеньями (линейные размерные цепи) ξ2 j =1. Коэффициент λ2 j = 1/9 при нормальном законе распределения отклонений (закон Гаусса). При распределении отклонений по закону треугольника (закон Симпсона) λ2 j = 1/6. При распределении отклонений по закону равной вероятности λ2 j = 1/3. Иногда в расчетах размерных цепей используют коэффициент относительного рассеяния К j = t∆ • λ j [7]. При наиболее часто используемом проценте риска 0,27 имеем по таблице 9.1 t∆ = 3 и с учетом значений коэффициента λ2 j коэффициент относительного рассеяния К j составляет: К j = 1 при законе распределения Гаусса; К j =1,22 при законе распределения Симпсона; К j =1,73 при законе распределения равной вероятности. При использовании коэффициента относительного рассеяния уравнение 9.11 принимает более простой вид для линейных размерных цепей при проценте риска 0,27
Среднее значение допуска составляющих звеньев вычисляют по формулам: при расчете по способу максимума - минимума
при расчете вероятностным способом
Для линейных размерных цепей формулы (11.13) и (11.14) приобретают более простой вид при решении способом равных допусков [44]: при расчете на максимум-минимум
при расчете вероятностным методом
Решая размерную цепь способом одного квалитета, определяют число единиц допуска в допуске размера (коэффициент точности) [44]: при полной взаимозаменяемости (на максимум-минимум)
при неполной взаимозаменяемости (вероятностный расчет)
При решении размерной цепи методом компенсации вычисляют наибольшую возможную компенсацию VK: VK =Т'А∆-ТА∆, (11.19) где Т'А∆ = ∑ТА j - производственный допуск замыкающего звена, равный сумме расширенных допусков звеньев размерной цепи. Число ступеней неподвижных компенсаторов:
где Ткомп. допуск на изготовление неподвижного компенсатора.
Составить размерную цепь и определить: - номинальное значение замыкающего звена; - верхнее и нижнее отклонение замыкающего звена; - допуск и предельные размеры замыкающего звена. Расчет произвести двумя способами: а) на max - min; б) вероятностным методом при риске 0,27 %, распределении размеров по нормальному закону при Kj = 1; αj = 0. Исходные данные: А1 = 50js12; А2 = 110h12; А3 = 25jsl2. Решение. Задача относится к числу обратных и имеет однозначное решение. Составляем схему размерной цепи. Замыкающим звеном этой размерной цепи является осевой размер, получающийся последним в результате изготовления. Таким размером является осевой размер утолщения валика. Схема размерной цепи приведена на рисунке 9.4.
По ГОСТ 25346-89 (Таблицы А.2 – А.4) находим величины допусков и отклонений звеньев и наносим их на схему: A1 = 50jsl2(±0,125); А2 = 110hl2(-0,35); А3 = 25jsl2(±0,105). Выявляем увеличивающие и уменьшающие звенья размерной цепи. Зададим замыкающему звену направление стрелкой налево (рисунок 9.5).
Используя правило обхода по замкнутому контуру устанавливаем, что звенья А1 и А3 уменьшающие (направление стрелок обхода по контуру совпадает с направлением стрелки замыкающего звена), а звено А2 - увеличивающее. Способ "а" (расчет на max - min) Номинальное значение замыкающего звена находим по формуле (9.2)
Допуск замыкающего звена (формула 9.3) с учетом того, что для линейных размерных цепей |ξ j | = 1:
Верхнее отклонение замыкающего звена (формула 9.7)
Нижнее отклонение замыкающего звена (формула 9.8)
Проверка:
Отклонения определены правильно. Предельные размеры замыкающего звена (формулы 9.9 и 9.10):
Размер замыкающего звена Способ "б" (вероятностный расчет) Номинальное значение замыкающего звена А∆ вычисляется по формуле (9.2) и было определено выше АD = 35 мм. Допуск замыкающего звена находим по формуле (9.12) с учетом значения K j = 1 соответствующего нормальному закону распределения
Найдем координату середины поля допуска замыкающего звена (уравнение 9.4), предварительно определив координаты середин полей допусков составляющих звеньев. Схемы полей допусков размеров, составляющих цепь приведены на рисунке 9.6.
Рисунок 9.6
Верхнее отклонение замыкающего звена (уравнение 9.5):
Нижнее отклонение замыкающего (уравнение 9.6):
Предельные размеры замыкающего звена (уравнения 6.9 и 6.10)
Размер замыкающего звена
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 2063; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.158.110 (0.008 с.) |



 Aj - увеличивающее j-e составляющее звено размерной цепи А;
Aj - увеличивающее j-e составляющее звено размерной цепи А;
 Aj - уменьшающее j-e составляющее звено размерной цепи А;
Aj - уменьшающее j-e составляющее звено размерной цепи А;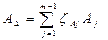 , (9.1)
, (9.1) , (9.2)
, (9.2)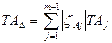 (9.3)
(9.3) , (9.4)
, (9.4) , (9.5)
, (9.5) . (9.6)
. (9.6) , (9.7)
, (9.7) . (9.8)
. (9.8) ; (9.9)
; (9.9) . (9.10)
. (9.10) , (9.11)
, (9.11) . (9.12)
. (9.12) (11.13)
(11.13) (11.14)
(11.14) ; (9.15)
; (9.15) . (9.16)
. (9.16) (9.17)
(9.17) (9.18)
(9.18) , (9.20)
, (9.20) Пример [28]. На рабочем чертеже детали (рисунок 9.3) среди прочих заданы продольные размеры A1; А2; А3 с известными номинальными значениями размеров и обозначениями их полей допусков.
Пример [28]. На рабочем чертеже детали (рисунок 9.3) среди прочих заданы продольные размеры A1; А2; А3 с известными номинальными значениями размеров и обозначениями их полей допусков.








 мм.
мм.






 мм.
мм.


