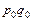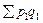Общая из индивидуальных средних

Рассчитывается по следующей формуле:

 

Степенные средние

Те средние величины, которые мы записали, относятся к степенным средним. В наиболее общем виде степенная средняя записывается следующим образом:

 

В зависимости от k и образуются разные виды средних.

Степень k	Вид средней	Формула расчета
k = 1	Арифметическая
k = 2	Квадратическая
k = 0	Геометрическая
k = -1	Гармоническая

 

Правило мажорантности:

 

 

Структурные средние

Величина средней определяется всеми значениями признака, встречающимися в данном ряду распределения. Различают такие структурные средние, как:

(1) мода

(2) медиана

(3) квартиль

(4) дециль

(5) перцентиль

Мода

Это значение признака, которое встречается в ряду распределения чаще, чем другие его значения.

В дискретном ряду распределения значения моды определяются визуально. Если же ряд распределения задан как интервальный, то значение моды рассчитывается по следующей формуле:

 

 

– нижняя граница модального интервала,

– величина модального интервала,

– частота (вес) интервала, предшествующего модальному,

– частота модального интервала,

– частота интервала, следующего за модальным.

 

Медиана

Это центральное значение признака, им обладает центральный член ранжированного ряда.

Прежде всего определяется порядковый номер медианы по формуле
и строят ряд накопленных частот. Накопленной частоте, которая равна порядковому номеру медианы или первая его превышает, в дискретном вариационном ряду соответствует значение медианы, а в интервальном – медианный интервал.

Для интервального ряда медиана рассчитывается по следующей формуле:

 

 

– нижняя граница медианного интервала,

– величина медианного интервала,

– сумма частот (весов) ряда,

– сумма накопленных частот (весов) в интервале, предшествующем медианному,

– частота медианного интервала.

 

Квартиль

Первый квартиль вычисляется по формуле:

 

– нижняя граница квартильного интервала,

– величина квартильного интервала,

– номер квартильного признака,

– сумма накопленных частот (весов) в интервалах, предшествующих квартильному,

– частота квартильного интервала.

 

Аналогично рассчитывается третий квартиль. Второй же квартиль равен медиане.

 

Дециль

Рассчитывается по аналогии с расчетом квартиля. Можно найти девять децилей.

 

Средняя должна исчисляться не просто тогда, когда есть вариация признака, а тогда, когда мы располагаем качественно однородным вариационным рядом. Среднюю как обобщающую характеристику нельзя применять к таким совокупностям, отдельные части которых подчиняются различным законам распределения (или) развития в отношении величины распределяемого признака.

Показатели вариации

 

 

Необходимость расчета показателей вариации

Средняя представляет собой обобщающую статистическую характеристику, в которой получает количественное выражение типичный уровень признака, которым обладают члены изучаемой совокупности. Но одной средней нельзя отобразить все характерные черты статистического распределения. Возможны случаи совпадения средних арифметических при разном характере распределения.

Показатели вариации используются для характеристики и упорядочения статистических совокупностей.

 

Абсолютные показатели вариации

Для измерения размера вариации используются следующие абсолютные показатели: размах, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение.

Размах

 

Величина его целиком зависит от случайности распределения крайних членов ряда, и значение подавляющего большинства членов ряда не учитывается, в то время как вариация связана с каждым значением члена ряда.

Такие показатели, которые представляют собой средние, полученные из отклонений индивидуальных значений признака от их средней величины, лишены этого недостатка.

Между индивидуальными отклонениями от средней и колеблемостью конкретного признака существует прямая зависимость. Чем сильнее колеблемость, тем больше абсолютные размеры отклонений от средней.

 

Дисперсия

Среднее линейное отклонение

 

 

Среднее квадратическое отклонение

 

Дисперсию можно подсчитать и по следующей формуле:

По этой формуле ленче считать дисперсию, когда имеешь дело с дискретным рядом распределения.

 

Годовой удой от одной коровы	Середина интервала	Число коров
до 2-х	1,5			-1,3	5,2	1,69	6,76
2-3	2,5			-0,3	0,6	0,09	0,18
3-4	3,5			+0,7	1,4	0,49	,98
4-5	4,5		4,5	+1,7	1,7	2,89	2,89
5 и более	5,5		5,5	+2,7	2,7	7,29	7,29
Сумма					11,6		18,1

 

 

Относительные показатели вариации

 

Коэффициент осцилляции –

 

Коэффициент относительного линейного отклонения –

 

Коэффициент вариации–

 

Дисперсия альтернативного признака

Альтернативный признак – это такой признак, которым одни члены обладают, а другие – нет.

доля единиц, не обладающих признаком

доля единиц, обладающих признаком

Виды дисперсий и правила их сложения

 

 

Межгрупповая дисперсия

Между отдельными видами дисперсий существует взаимосвязь, которую можно записать в виде правила сложения дисперсий:

 

Пример: Распределение сотрудников КБ по производительности труда

Расчет общей дисперсии

x	f	xf	x^2	x^2f

 

 

2. Расчет дисперсии по первой группе

x	f	xf	x^2	x^2f

 

3. Расчетдисперсии по второй группе

x	f	xf	x^2	x^2f

 

4. Расчет межгрупповой дисперсии

11,2		-2,325	5,405	135,140
17,4		3,875	15,015	225,234
				360,375

 

5. Расчет средней из индивидуальных дисперсий

 

Эмпирическое корреляционное отношение (ЭКО)

На основании правила сложения дисперсий вычисляется эмпирическое корреляционное отношение (ЭКО), которое равно квадратному корню из отношения межгрупповой дисперсии к общей:

 

Такой порядок вычисления обусловлен разложением общей вариации на вариацию, зависящую от фактора, положенного в основу группировки (в нашем примере – повышение и неповышение квалификации), которая численно равна межгрупповой дисперсии, и общую вариацию.

Межгрупповая дисперсия составляет часть общей дисперсии и складывается под влиянием только одного группировочного фактора. Именно поэтому подкоренное выражение показывает долю вариации за счет группировочного признака.

ЭКО изменяется в переделах от нуля до единицы. Чем ближе его значение к единице, тем большая доля вариации падает на группировочный признак.

В нашем случае

 

Некоторые математические свойства дисперсий

(1) При вычитании из всех значений признака некоторой постоянной величины дисперсия не изменится.

(2) При сокращении всех значений на постоянный множитель дисперсия уменьшится в раз.

(3) Средний квадрат отклонений значений признака от постоянной произвольной величины больше дисперсии признака на квадрат разности между средней арифметической и постоянной величиной.

 

На основании свойств дисперсии ее можно подсчитать способом отсчета от условного нуля и способом моментов.

 

Интервал
90-100				-30	-3	-6
100-110				-20	-2	-12
110-120				-10	-1	-8
120-130			2 250
130-140
140-150
150-160
160-170
170-180
			6 390

 

Экономические индексы

 

 

Понятие индексов

В статистике под индексом понимается относительная величина (показатель), выражающая изменение сложного экономического явления во времени, в пространстве или по сравнению с планом. В связи с этим различают динамические, территориальные индексы, а также индексы выполнения плана.

Многие общественные явления состоят из непосредственно несопоставимых явлений, поэтому основной вопрос – это вопрос сопоставимости сравниваемых явлений.

К какому бы экономическому явлению ни относились индексы, чтобы рассчитать их, необходимо сравнивать различные уровни, которые относятся либо к различным периодам времени, либо к плановому заданию, либо к различным территориям. В связи с этим различают базисный период (период, к которому относится величина, подвергаемая сравнению) и отчетный период (период, к которому относится сравниваемая величина). При исчислении важно правильно выбрать период, принимаемый за базу сравнения.

Индексы могут относиться либо к отдельным элементам сложного экономического явления, либо ко всему явлению в целом.

 

Индивидуальные индексы

Показатели, характеризующие изменение более или менее однородных объектов, входящих в состав сложного явления, называются индивидуальными индексами – i_x.

p – цена q – количество t – время T – численность f – з/п F – фонд з/п S – посевная площадь y – урожайность z – себестоимость

Индекс получает название по названию индексируемой величины.

В большинстве случаев в числителе стоит текущий уровень, а в знаменателе – базисный уровень. Исключением является индекс покупательной способности рубля.

 

Индексы измеряются либо в виде процентов (%), либо в виде коэффициентов.

 

Сводные индексы

Сложные явления, для которых рассчитывается сводный индекс, отличаются той особенностью, что элементы, их составляющие, неоднородны и, как правило, несоизмеримы друг с другом. Поэтому сопоставление простых сумм этих элементов невозможно. Сопоставимость может быть достигнута различными способами:

(1) сложные явления могут быть разбиты на такие простые элементы, которые в известной степени являются однородными;

(2) сравнение по стоимости, без разбиения на отдельные элементы.

Цель теории индексов – изучение способов получения относительных величин, используемых для расчета общего изменения ряда разнородных явлений.