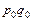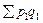Российской коллекции рефератов (с) 1996

Учебный материал

РОССИЙСКОЙ КОЛЛЕКЦИИ РЕФЕРАТОВ (с) 1996

http://referat.students.ru; http://www.referats.net; http://www.referats.com

 

 

Содержание

 

 

Тема № 1. Предмет и метод статистики3

История, пути и направления статистической науки 3

Предмет статистики 3

Отрасли статистики 4

Метод статистики 4

Закон больших чисел 4

Статистическая закономерность 5

Задачи статистики 5

Организация государственной статистики в РФ 5

Ряды распределения 5

 

Тема № 2. Статистическое наблюдение6

Понятие статистического наблюдения 6

Формы статистического наблюдения 6

Виды статистического наблюдения 6

Виды несплошного наблюдения 6

Способы статистического наблюдения 7

Программно-методологические вопросы статистического наблюдения 7

 

Тема № 3. Сводка и группировка8

Статистическая сводка 8

Статистическая группировка 8

Виды группировок 8

Система группировок 10

 

Тема № 4. Статистические таблицы11

Понятие статистической таблицы 11

Виды таблиц в зависимости от разработки подлежащего 11

Виды таблиц по характеру сказуемого 11

Элементы таблицы 11

Запись цифр в таблицах 11

 

Тема № 5. Абсолютные и относительные величины12

Абсолютные статистические величины 12

Относительные статистические величины 12

Виды относительных величин 13

 

Тема № 6. Графический метод14

Понятие графика 14

Схема статистических графиков по форме графического способа 14

Схема статистических графиков по способу и задачам построения 14

Основные правила построения графиков 14

 

Тема № 7. Средние величины15

Сущность и задачи средних величин 15

Расчет средней 15

Средняя арифметическая 16

Способ моментов 16

Средняя гармоническая 17

Общая из индивидуальных средних 17

Степенные средние 17

Структурные средние 17

 

Тема № 8. Показатели вариации19

Необходимость расчета показателей вариации 19

Абсолютные показатели вариации 19

Относительные показатели вариации 20

Дисперсия альтернативного признака 20

Виды дисперсий и правила их сложения 20

Эмпирическое корреляционное отношение (ЭКО) 21

Некоторые математические свойства дисперсий 21

 

Тема № 9. Экономические индексы23

Понятие индексов 23

Индивидуальные индексы 23

Сводные индексы 23

Средние индексы 24

Цепные и базисные индексы с постоянными и переменными весами 24

Индексы постоянного состава, переменного состава и структурных сдвигов 25

Индексы Пааше, Ласпейреса и "идеальный индекс" Фишера 26

Территориальные индексы 26

Индексы планового задания и выполнения плана 26

 

Тема № 10. Ряды динамики27

Задачи статистики в области рядов динамики 27

Понятие и виды рядов динамики 27

Несопоставимость уровней рядов динамики 27

Показатели изменения уровней ряда 28

Средние характеристики ряда динамики 28

Выявление основной тенденции развития динамических рядов 29

Прогнозирование и интерполяция 30

 

Тема № 11. Статистическое измерение связи31

Задачи статистики в изучении связи.
Взаимосвязанные признаки и их классификация. 31

Виды и формы связей, различаемые в статистике. 31

Методы изучения связей 31

 

Тема № 12. Выборочный метод36

Основы выборочного метода 36

Ошибки выборки 37

Средняя ошибка выборки 37

Предельная ошибка выборки 37

Основные виды выборки, способы отбора 38

Примеры задач 38

Численность выборки 39

Повторный групповой отбор 39

Многоступенчатый отбор 40

Бесповторный отбор 40

Определение границ изменения генеральной средней 40

Предмет и метод статистики

 

 

История, пути и направления статистической науки

Термин "статистика" появился в середине 18 века. Означал "государствоведение". Получил распространение в монастырях. Постепенно приобрел собирательное значение.

С одной стороны, статистика – это совокупность числовых показателей, характеризующих общественные явления и процессы (статистика труда, статистика транспорта).

С другой – под статистикой понимается практическая деятельность по сбору, обработке, анализу данных по различным направлениям общественной жизни.

С третьей стороны, статистика – это итоги массового учета, опубликованные в различных сборниках.

Наконец, в естественных науках статистикой называются методы и способы оценки соответствия данных массового наблюдения математическим формулам.

Таким образом, статистика – это общественная наука, изучающая количественную сторону массовых общественных явлений в неразрывной связи с их качественной стороной.

 

Ученые, внесшие вклад в развитие статистики

– Уильям Петти – основатель статистики. Его заслуга в том, что он впервые применил числовой метод для анализа закономерностей общественной жизни. Работа – "Политическая арифметика".

– Адольф Кетле – бельгийский статистик. Доказал, что даже кажущиеся случайности общественной жизни обладают внутренней закомерностью и необходимостью.

– К.Ф. Герман – русский статистик ("Всеобщая теория статистики").

– В.И. Ленин – теория группировок, теория статистического наблюдения.

– Целый ряд других ученых.

 

 

Предмет статистики

Статистика изучает количественно определенные качествамассовыхсоциально-экономических явлений. 1 2 3

Существует несколько точек зрения на статистику как на науку:

(1) Статистика – это универсальная наука, изучающая массовые явления природы и общества.

(2) Статистика – это методологическая наука, разрабатывающая методы исследования для других наук.

(3) Статистика – это общественная наука.

 

Явления общественной жизни – это сложное сочетание различных элементов.

– Общественные явления обладают вполне конкретными размерами.

– Общественным явлениям присущи определенные количественные соотношения, и существуют они независимо от того, изучает ли их статистика или нет.

 

Размеры и соотношения количества и качества отдельных явлений статистика выражает при помощи определенных понятий, статистических показателей. Числовое значение показателя, относящееся к определенному месту и времени, называют величиной показателя.

 

 

Отрасли статистики

Общая теория статистики – это лишь фундамент. В любой своей части она связана с другими науками.

 

Общая теория статистики

Демографическая статистика

Экономическая статистика

Статистика образования

Медицинская статистика

Спортивная статистика

Статистика труда

Статистика заработной платы

Статистика мат.-техн. снабжения

Статистика транспорта

Статистика связи

Статистика финансового кредита

Высшие финансовые вычисления

Статистика денежного обращения

Статистика валютных курсов

Прочие

 

Статистика также разрабатывает теорию наблюдения.

 

 

Метод статистики

Метод статистики предполагает следующую последовательность действий:

– разработка статистической гипотезы,

– статистическое наблюдение,

– сводка и группировка статистических данных,

– анализ данных,

– интерпретация данных.

Прохождение каждой стадии связано с использованием специальных методов, объясняемых содержанием выполняемой работы.

 

 

Закон больших чисел

Массовый характер общественных законов и своеобразие их действий предопределяет необходимость исследования совокупных данных.

Закон больших чисел порожден особыми свойствами массовых явлений. Последние в силу своей индивидуальности, с одной стороны, отличаются друг от друга, а с другой – имеют нечто общее, обусловленное их принадлежностью к определенному классу, виду. Причем единичные явления в большей степени подвержены воздействию случайных факторов, ежели их совокупность.

Статистическая закономерность

Статистические закономерности изучают распределение единиц статистического множества по отдельным признакам под воздействием всей совокупности факторов.

Статистическая закономерность выступает как объективная закономерность сложного массового процесса и является формой причинной связи. Она обнаруживается в итоге массового статистического наблюдения. Этим обуславливается ее связь с законом больших чисел.

Статистическая закономерность с определенной вероятностью гарантирует устойчивость средних величин при сохранении постоянного комплекса условий, порождающих данное явление.

 

 

Задачи статистики

(1) Разработка системы гипотез, характеризующих развитие, динамику, состояние социально-экономических явлений.

(2) Организация статистической деятельности.

(3) Разработка методологии анализа.

(4) Разработка системы показателей для управления хозяйством на макро- и микроуровне.

(5) Популяризовать данные статистического наблюдения.

 

 

Ряды распределения

Рядами распределения называются группировки особого вида, при которых по каждому признаку, группе признаков или классу признаков известны численность единиц в группе либо удельный вес этой численности в общем итоге.

Ряды распределения могут быть построены или по количественному, или по атрибутивному признаку.

Ряды распределения, построенные по количественному признаку, называются вариационными рядами. Ряд распределения может быть построен по непрерывно варьирующему признаку (когда признак может принимать любые значения в рамках какого-либо интервала) и по дискретно варьирующему признаку (принимает строго определенные целочисленные значения).

Непрерывно варьирующий признак изображается графически при помощи гистограммы. Дискретный же ряд распределения графически представляется в виде полигона распределения.

Статистическое наблюдение

 

 

Виды несплошного наблюдения

 

– Анкетный способ

 

Исследуются какие-то осредненные показатели и распространяются на всю совокупность.

 

 

– Метод основного массива

 

Исследуются наиболее крупные единицы изучаемого явления.

– Метод направленного долевого отбора

 

– Выборочный метод

 

Его основой является случайный отбор. Результат гарантируется с определенной вероятностью р.

 

– Монографический метод

Подвергаются тщательному исследованию отдельные единицы совокупности, обычно представители новых типов, либо самые лучшие (худшие) единицы. Результаты переносятся на всю совокупность. Позволяет выявить тенденции.

 

 

Сводка и группировка

 

 

Статистическая сводка

Статистическая сводка – это операция по обработке собранных данных, которые выражаются в виде показателей, относящихся к каждой единице объекта статистического наблюдения. В результате сводки эти данные превращаются в систему статистических таблиц и промежуточных итогов. По результатам сводки можно выявить наиболее типичные черты и закономерности изучаемых явлений.

Предварительно составляется программа и план сводки.

В программе определяется подлежащее и сказуемое сводки. Подлежащее составляет вся совокупность группы или части, на которые разбивается совокупность. Сказуемое – это те показатели, которые характеризуют каждую группу, часть или всю совокупность в целом.

План сводки – содержит организационные вопросы.

 

 

Статистическая группировка

Статистическая группировка – это метод исследования массовых общественных явлений путем выделения и ограничения однородных групп, через которые раскрываются существенные черты и особенности состояния и развития всей совокупности.

Основные задачи, которые решаются с помощью группировок:

(1) выделение социально-экономических типов,

(2) изучение структуры социально-экономических явлений,

(3) выявление связи между явлениями.

Важнейшие проблемы:

(1) Определение группировочного признака (основания группировки).

Группировочный признак – это признак, по которому происходит определение единиц в группе. Его выбор зависит от цели группировки и существа данного явления.

(2) Выделение числа групп.

Число групп определяется с таким расчетом, чтобы в каждую группу попало достаточно большое число единиц.

(3) Интервалы

Интервалы могут быть равными и неравными. Последние в свою очередь делятся на равномерно возрастающие и равномерно убывающие.

 

 

Виды группировок

 

(1) Типологические группировки

Их задача – выявление социально-экономических типов или однородных в существенном отношении групп.

№ п/п	Социально-экономические типы	Мужчины	Женщины
1.	Работники	–	–	–	–
2.	Крестьяне	–	–	–	–
3.	Служащие	–	–	–	–

(2) Структурные группировки

Их задача – изучение состава отдельных типических групп при помощи объединения единиц совокупности, близких друг к другу по величине группировочного признака.

№ п/п	Количество посадочных мест	Количество столов	Число занятых	Товарооборот на 1 место
1.	до 25	–	–	–
2.	16 – 50	–	–	–
3.	51 – 70	–	–	–
4.	71 – 100	–	–	–

 

(3) Аналитические группировки

Их задача – выявления влияния одних признаков на другие (выявить связь между социально-экономическими явлениями).

№ п/п	Группы магазинов по числу рабочих мест	Число магазинов	Товарооборот
на 1 работника	на 1 раб. место
1.	до 5		12,0	13,0
2.	6 – 10		14,0	16,0
3.	11 – 15		15,0	17,0
4.	16 – 20		30,0	39,0
5.	21 – 25		31,0	42,0

 

(4) Комбинационные группировки

В них производится разделение совокупности на группы по двум или более признакам. При этом группы, образованные по одному признаку, разбиваются на подгруппы по другому признаку.

Такие группировки дают возможность изучить структуру совокупности по нескольким признакам одновременно.

№ п/п	Группы предприятий по объему основных фондов	Оплата труда в рублях	Пол	Количество единиц
1.	до 200	100 – 120	М	–
Ж	–
120 – 140	М	–
Ж	–
140 – 160	М	–
Ж	–
2.	200 – 400	100 – 120	М	–
Ж	–
120 – 140	М	–
Ж	–
140 – 160	М	–
Ж	–
3.	400 – 600	100 – 120	М	–
Ж	–
120 – 140	М	–
Ж	–
140 – 160	М	–
Ж	–
4.	600 – 800	100 – 120	М	–
Ж	–
120 – 140	М	–
Ж	–
140 – 160	М	–
Ж	–

 

Система группировок

Социально-экономический анализ предполагает использование системы простых и комбинационных группировок.

Также очень часто прибегают к вторичной группировке – перегруппировка уже сгруппированных данных. Вторичная группировка может быть проведена методом простого укрупнения интервала.

Часто также используется процентная перегруппировка.

 

Пример: Группировка фермерских хозяйств по наличию скота.

Исходные данные:

№ п/п	Группы хозяйств по числу голов	% фермерских хозяйств	% поголовья	% по всему кол-ву скота
1.	без голов	26,4	2,8	9,9
2.	с 1-й головой	20,3	9,5	8,9
3.	с 2-мя головами	14,6	11,8	11,1
4.	с 3-мя –– " ––	9,3	10,5	9,8
5.	с 4-мя –– " ––	8,3	12,1	11,2
6.	с 5-ю –– " ––	21,1	53,3	56,1
	Всего:

 

 

Процентная перегруппировка

№ п/п	Группы хозяйств по уровню развития	% фермерских хозяйств	% поголовья	% по всему кол-ву скота
1.	Низкий		14,9	21,3
2.	Средний		34,6	32,5
3.	Высокий		50,5	53,2
	Всего:

 

Расчеты:

1. 26,4 + 20,3 = 46,7

2. 50 – 46,7 = 3,3

3. 3,3 / 14,6 = 0,226

4. 0,226 * 11,8 = 2,6 0,226 * 11,1 = 2,5

5. 2,8 + 9,5 + 2,6 = 14,9 9,9 + 8,9 + 2,5 = 21,3

 

6. 11,3 + 9,3 + 8,3 = 28,9

7. 30 – 28,9 = 1,1

8. 1,1 / 21,1 = 0,052

9. 0,052 * 53,3 = 2,8 0,052 * 56,1 = 2,9

10. (11,8 – 2,6) + 10,5 + 12,1 + 2,8 = 34,6 (11,1 – 2,5) + 9,8 + 11,2 + 2,9 = 32,5

 

11. 53,3 – 2,8 = 50,5 56,1 – 2,9 = 53,2

Статистические таблицы

 

 

Элементы таблицы

– Название.

– Единицы измерения.

– Нумерация граф и строк.

 

Запись цифр в таблицах

Если одно из числовых выражений данного признака равно нулю, то пересечение соответствующей графы и строки перечеркивается.

Если числовые значения признака неизвестны, то в пересечении графы и строки ставится многоточие.

Если пересечение графы и строки не имеет смысла, то ставится "Х".

Если в таблице проценты по отношению к какому-либо предыдущему году, то этот год должен быть показан в таблице, несмотря на указание его в заголовке.

Типы абсолютных величин

(1) Натуральные – такие единицы, которые отражают величину предметов, вещей в физических мерах (вес, объем, площадь и т.д.).

(2) Денежные (стоимостные) – используются для характеристики многих экономических показателей в стоимостном выражении.

(3) Трудовые – используются для определения затрат труда (человеко-час, человеко-день)

(4) Условно-натуральные –единицы, которые используются для сведения воедино нескольких разновидностей потребительных стоимостей (т.у.т = 29,3 МДж/кг; мыло 40 % жирности).

Виды абсолютных величин

– Индивидуальные – отражают размеры количественных признаков у отдельных единиц изучаемой совокупности.

– Общие – выражают размеры, величину количественных признаков у всей изучаемой совокупности в целом.

Абсолютные величины отражают наличие тех или иных ресурсов, это основа материального учета. Они наиболее объективно отражают развитие экономики.

Абсолютные величины являются основой для расчета разных относительных статистических показателей.

 

 

Виды относительных величин

Все применяемые на практике относительные статистические величины подразделяются на следующие виды.

 

Графический метод

 

 

Понятие графика

Средние величины

Расчет средней

К расчету средней предъявляются два основных требования:

(1) Среднюю нужно рассчитывать так, чтобы она погашала то, что мешает выявлению характерных черт и закономерностей в развитии явления, а не затушевывала развитие.

(2) Средняя может быть вычислена только для однородной совокупности. Средняя, вычисленная для неоднородной совокупности, называется огульной.

Одинаковые по форме и технике вычисления средние в одних случаях могут быть огульными, а в других – общими в зависимости от того, с какой целью они интерпретируются.

Говоря о методологии исчисления средних, не надо забывать, что средняя всегда дает обобщенную характеристику лишь по одному признаку. Каждая же единица совокупности имеет много признаков. Поэтому необходимо рассчитывать систему средних, чтобы охарактеризовать явление со всех сторон.

Расчет средних величин производится по правилам, которые разрабатываются математической статистикой. Задача ОТС – дать смысловую, преимущественно экономическую интерпретацию результатам расчетов, произведенных по формулам.

Признак, по которому производится осреднение, называется осредняемым признаком –. Величина осредняемого признака у каждой единицы совокупности называется ее индивидуальным значением.

Значение признака, которое встречается у групп единиц или у отдельных единиц и не повторяется, называется вариантом признака –

Средняя величина этих вариантов, или просто средняя, обозначается.

 

Средняя арифметическая

Простая средняя арифметическая для ряда данных рассчитывается по формуле:

 

Но можно также рассчитать среднюю арифметическую взвешенную как:

 

Свойства средней арифметической:

(1) Сумма отклонений различных значений признака от среднеарифметической равна нулю:

(2) Если от каждого варианта вычесть или к каждому варианту прибавить какое-либо произвольное постоянное число, то средняя увеличится или уменьшится на то же самое число.

(3) Если каждый вариант умножить (разделить) на какое-либо произвольное постоянное число, то средняя увеличится (уменьшится) во столько же раз.

(4) Если веса, или частоты, разделить или умножить на какое-либо произвольное постоянное число, то величина средней не изменится. Это свойство дает возможность заменять веса их удельными весами:

 

 

Способ моментов

Часто мы сталкиваемся с расчетом средней арифметической упрощенным способом. В этом случае используются свойства средней величины. Метод упрощенного расчета называется способом моментов, либо способом отсчета от условного нуля.

Способ моментов предполагает следующие действия:

1) Если возможно, то уменьшаются веса.

2) Выбирается начало отсчета – условный нуль. Обычно выбирается с таким расчетом, чтобы выбранное значение признака было как можно ближе к середине распределения. Если распределение по своей форме близко к нормальному, но за начало отсчета выбирают признак, обладающий наибольшим весом.

3) Находятся отклонения вариантов от условного нуля.

4) Если эти отклонения содержат общий множитель, то рассчитанные отклонения делятся на этот множитель.

5) Находится среднее значение признака по следующей формуле

	Пример:

до 70			-30	-3	-45
70-80			-20	-2	-34
80-90			-10	-1	-13
90-100
100-110
110-120
120-130
130-140
140 и более
Сумма					-12

 

Средняя гармоническая

Расчет средней гармонической связан с двумя причинами:

1) Не всегда возможно рассчитать среднюю арифметическую на основе имеющихся данных.

2) Расчет средней гармонической проводить более удобно.

 

Расчет простой средней гармонической:

 

Расчет средней гармонической взвешенной:

 

Пример:

Такой расчет имеет определенные трудности, которые заключаются в том, что не всегда ясно можно трактовать условие поставленной задачи. Поэтому перед тем, как приступать к расчету средней, необходимо разобраться в экономическом смысле данных, которыми вы располагаете.

Базисный	Отчетный
Фонд з/п	Среднеспис. з/п	Среднеспис. з/п	Среднеспис. численность
xf	х	x	f
Средняя гармоническая	Средняя арифметическая

 

Степенные средние

Те средние величины, которые мы записали, относятся к степенным средним. В наиболее общем виде степенная средняя записывается следующим образом:

 

В зависимости от k и образуются разные виды средних.

Степень k	Вид средней	Формула расчета
k = 1	Арифметическая
k = 2	Квадратическая
k = 0	Геометрическая
k = -1	Гармоническая

 

Правило мажорантности:

 

 

Структурные средние

Величина средней определяется всеми значениями признака, встречающимися в данном ряду распределения. Различают такие структурные средние, как:

(1) мода

(2) медиана

(3) квартиль

(4) дециль

(5) перцентиль

Мода

Это значение признака, которое встречается в ряду распределения чаще, чем другие его значения.

В дискретном ряду распределения значения моды определяются визуально. Если же ряд распределения задан как интервальный, то значение моды рассчитывается по следующей формуле:

 

 

– нижняя граница модального интервала,

– величина модального интервала,

– частота (вес) интервала, предшествующего модальному,

– частота модального интервала,

– частота интервала, следующего за модальным.

 

Медиана

Это центральное значение признака, им обладает центральный член ранжированного ряда.

Прежде всего определяется порядковый номер медианы по формуле
и строят ряд накопленных частот. Накопленной частоте, которая равна порядковому номеру медианы или первая его превышает, в дискретном вариационном ряду соответствует значение медианы, а в интервальном – медианный интервал.

Для интервального ряда медиана рассчитывается по следующей формуле:

 

 

– нижняя граница медианного интервала,

– величина медианного интервала,

– сумма частот (весов) ряда,

– сумма накопленных частот (весов) в интервале, предшествующем медианному,

– частота медианного интервала.

 

Квартиль

Первый квартиль вычисляется по формуле:

 

– нижняя граница квартильного интервала,

– величина квартильного интервала,

– номер квартильного признака,

– сумма накопленных частот (весов) в интервалах, предшествующих квартильному,

– частота квартильного интервала.

 

Аналогично рассчитывается третий квартиль. Второй же квартиль равен медиане.

 

Дециль

Рассчитывается по аналогии с расчетом квартиля. Можно найти девять децилей.

 

Средняя должна исчисляться не просто тогда, когда есть вариация признака, а тогда, когда мы располагаем качественно однородным вариационным рядом. Среднюю как обобщающую характеристику нельзя применять к таким совокупностям, отдельные части которых подчиняются различным законам распределения (или) развития в отношении величины распределяемого признака.

Показатели вариации

 

 

Размах

 

Величина его целиком зависит от случайности распределения крайних членов ряда, и значение подавляющего большинства членов ряда не учитывается, в то время как вариация связана с каждым значением члена ряда.

Такие показатели, которые представляют собой средние, полученные из отклонений индивидуальных значений признака от их средней величины, лишены этого недостатка.

Между индивидуальными отклонениями от средней и колеблемостью конкретного признака существует прямая зависимость. Чем сильнее колеблемость, тем больше абсолютные размеры отклонений от средней.

 

Дисперсия

Среднее линейное отклонение

 

 

Расчет общей дисперсии

x	f	xf	x^2	x^2f

 

 

2. Расчет дисперсии по первой группе

x	f	xf	x^2	x^2f

 

3. Расчетдисперсии по второй группе

x	f	xf	x^2	x^2f

 

4. Расчет межгрупповой дисперсии

11,2		-2,325	5,405	135,140
17,4		3,875	15,015	225,234
				360,375

 

5. Расчет средней из индивидуальных дисперсий

 

Экономические индексы

 

 

Понятие индексов

В статистике под индексом понимается относительная величина (показатель), выражающая изменение сложного экономического явления во времени, в пространстве или по сравнению с планом. В связи с этим различают динамические, территориальные индексы, а также индексы выполнения плана.

Многие общественные явления состоят из непосредственно несопоставимых явлений, поэтому основной вопрос – это вопрос сопоставимости сравниваемых явлений.

К какому бы экономическому явлению ни относились индексы, чтобы рассчитать их, необходимо сравнивать различные уровни, которые относятся либо к различным периодам времени, либо к плановому заданию, либо к различным территориям. В связи с этим различают базисный период (период, к которому относится величина, подвергаемая сравнению) и отчетный период (период, к которому относится сравниваемая величина). При исчислении важно правильно выбрать период, принимаемый за базу сравнения.

Индексы могут относиться либо к отдельным элементам сложного экономического явления, либо ко всему явлению в целом.

 

Индивидуальные индексы

Показатели, характеризующие изменение более или менее однородных объектов, входящих в состав сложного явления, называются индивидуальными индексами – i_x.

p – цена q – количество t – время T – численность f – з/п F – фонд з/п S – посевная площадь y – урожайность z – себестоимость

Индекс получает название по названию индексируемой величины.

В большинстве случаев в числителе стоит текущий уровень, а в знаменателе – базисный уровень. Исключением является индекс покупательной способности рубля.

 

Индексы измеряются либо в виде процентов (%), либо в виде коэффициентов.

 

Сводные индексы

Сложные явления, для которых рассчитывается сводный индекс, отличаются той особенностью, что элементы, их составляющие, неоднородны и, как правило, несоизмеримы друг с другом. Поэтому сопоставление простых сумм этих элементов невозможно. Сопоставимость может быть достигнута различными способами:

(1) сложные явления могут быть разбиты на такие простые элементы, которые в известной степени являются однородными;

(2) сравнение по стоимости, без разбиения на отдельные элементы.

Цель теории индексов – изучение способов получения относительных величин, используемых для расчета общего изменения ряда разнородных явлений.

Товар	Базисный	Отчетный
...
n

Индекс цены товарооборота

 

Проблема выбора весов

Если индексируемой величиной является качественный признак, то вес принимается на уровне текущего периода.

Если же индексируемой величиной является количественный признак, то вес принимается на уровне базисного периода.

Такой выбор весов позволяет записать следующую связь:

Сводные индексы в агрегатной форме позволяют нам измерить не только относительное изменение отдельных элементов изучаемого явления и явления в целом в текущем периоде по сравнению с базисным, но и абсолютное изменение.

Например, если мы вычтем из числителя индекса цены его знаменатель, то мы получим абсолютное изменение стоимости товарооборота в результате изменения цен:

 

 

То же самое можно сделать для индекса физического объема и для индекса товарооборота.

 

Средние индексы

Агрегатная форма индекса – одна из важнейших, но не единственная. В практических расчетах очень часто используются средние индексы. Это связано с тем, что, например, в индексе цены пересчет продукции, реализованной в текущем периоде, в базисные цены практически очень сложен. В то время как индивидуальные индексы цены на практике разрабатываются постоянно.

 

 

Агрегатный индекс цены тождественен среднему гармоническому индексу цены.

Агрегатный индекс физического объема тождественен среднему арифметическому индексу физического объема.

Проблема связана лишь с прочтением условия задачи.