
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дане тіло має об'єм v, якщо існують прості тіла, що містять його, і прості тіла, що містяться в ньому, з об'ємами, що як завгодно мало відрізняються від V.Содержание книги
Поиск на нашем сайте Застосуємо це визначення до знаходження об'єму циліндра з радіусом основи R і висотою Н. Мал.7
Побудуємо дві прямі призми з основами Р и Р' і висотою Н, яка дорівнює висоті циліндра. Перша призма містить циліндр, а друга призма міститься в циліндрі. Оскільки при необмеженому збільшенні n площі основ призм необмежено наближаються до площі основи циліндра S, то їх об'єми необмежено наближаються до SН. Згідно з визначенням об'єм циліндра V = SН= Отже, об'єм циліндра дорівнює добутку площі основи на висоту.
2. Побудуємо два многокутники в площині основи конуса: многокутник Р, що містить основу конуса, і багатокутник Р', що міститься в основі конуса (мал.8). Побудуємо дві піраміди з основи Р и Р' і з вершинами у вершині конуса. Перша піраміда містить конус, а друга міститься в конусі.
V = Мал. 8
Мал. 9
Тілом обертання в найпростішому випадку називається таке тіло, яке площинами, перпендикулярними до деякої прямої (осі обертання), перетинається по кругах з центрами на цій прямій. Круговий циліндр, конус, куля — приклади тіл обертання. Знайдемо формулу для обчислення об'єму тіла обертання. Проведемо площину через вісь тіла і введемо в цій площині декартові координати х, y, прийнявши вісь тіла за вісь х (мал. 10). Площина ху перетинає поверхню тіла по лінії, для якої вісь х є віссю симетрії. Нехай у = f(х) — рівняння тієї частини лінії, яка перебуває над віссю х.
Мал.10 При наближенні висоти h до нуля ліва і права частини останньої нерівності прямують до однієї і тієї самої величині V′(х) = За відомою формулою аналізу V(b) - V(a) = Ця формула і виражає об'єм частини тіла, що знаходиться між паралельними площинами х = a і х = b.
Застосуємо виведену формулу для об'єму тіл обертання до обчислення об'єму кулі. Введемо декартові координати, прийнявши центр кулі за початок координат (мал. 11). Площина ху перетинає поверхню кулі радіуса R по колу, яке, як відомо, задається рівнянням
Півколо, розташоване над віссю х, задається рівнянням у = f(х) = + Тому об'єм кулі знаходимо за формулою V = 78. Мал.11 Кульовим сегментом називається частина кулі, що відтинається від нього площиною. Формулу для об'єму кульового сегмента одержують аналогічно формулі об'єму кулі (мал.12):
V = де R - радіус кулі, а Н — висота кульового сегмента.
Мал.12
V = де R - радіус кулі, Н - висота відповідного кульового сегмента.
Мал.13
|
||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 419; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

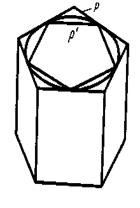 У процесі виведення формули для площі круга ми побудували такі два n -кутники (один, який містить круг, а інший міститься у крузі), що їх площі при необмеженім збільшенні n необмежено наближалися до площі круга. Побудуємо такі многокутники для круга в основі циліндра. Нехай Р — многокутник, що містить круг, а Р' — многокутник, який міститься у крузі. (мал. 7).
У процесі виведення формули для площі круга ми побудували такі два n -кутники (один, який містить круг, а інший міститься у крузі), що їх площі при необмеженім збільшенні n необмежено наближалися до площі круга. Побудуємо такі многокутники для круга в основі циліндра. Нехай Р — многокутник, що містить круг, а Р' — многокутник, який міститься у крузі. (мал. 7).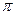 R2Н.
R2Н.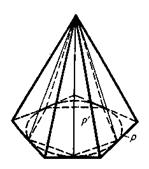 Як відомо, існують такі многокутники Р и Р', площі яких при необмеженому збільшенні числа їх сторін n необмежено наближаються до площі кругу в основі конуса. Для таких многокутників об'єми побудованих пірамід необмежено наближаються до
Як відомо, існують такі многокутники Р и Р', площі яких при необмеженому збільшенні числа їх сторін n необмежено наближаються до площі кругу в основі конуса. Для таких многокутників об'єми побудованих пірамід необмежено наближаються до  SH, де S - площа основи конуса, а H — його висота. Згідно з визначенням звідси випливає, що об'єм конуса
SH, де S - площа основи конуса, а H — його висота. Згідно з визначенням звідси випливає, що об'єм конуса Отже, об'єм конуса дорівнює третині добутку площі основи на висоту.
Отже, об'єм конуса дорівнює третині добутку площі основи на висоту.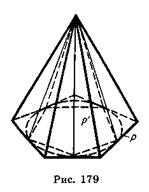 Об'єм зрізаного конуса дорівнює: V =
Об'єм зрізаного конуса дорівнює: V = 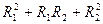 )
)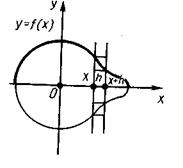 Проведемо через точку (х, 0) площину, перпендикулярну до осі х, і позначимо через V(х) об'єм частини тіла, що лежить ліворуч від цієї площини. Тоді V(х) є функцією від х. Різниця V(х+h) - V(х) становить об'єм шару тіла товщиною h між двома площинами, перпендикулярними до осі х, які проходять через точки з абсцисами х і х+h. Нехай М — найбільше, а m — найменше значення функції f(х) на відрізку [х, х+h ]. Тоді розглянутий шар тіла містить циліндр з радіусом m, висотою h і вміщується у циліндрі з радіусом М и тією ж висотою h. Тому
Проведемо через точку (х, 0) площину, перпендикулярну до осі х, і позначимо через V(х) об'єм частини тіла, що лежить ліворуч від цієї площини. Тоді V(х) є функцією від х. Різниця V(х+h) - V(х) становить об'єм шару тіла товщиною h між двома площинами, перпендикулярними до осі х, які проходять через точки з абсцисами х і х+h. Нехай М — найбільше, а m — найменше значення функції f(х) на відрізку [х, х+h ]. Тоді розглянутий шар тіла містить циліндр з радіусом m, висотою h і вміщується у циліндрі з радіусом М и тією ж висотою h. Тому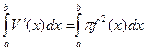 , a < b.
, a < b.
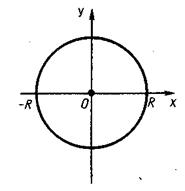 х2 + у2 = R2.
х2 + у2 = R2.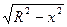 , - R < х ≤ R.
, - R < х ≤ R.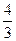
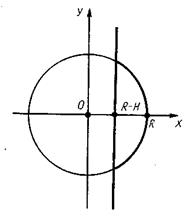
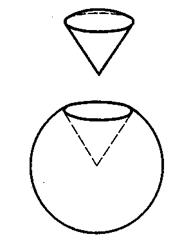 Кульовим сектором називається тіло, одержане з кульового сегмента і конуса в такий спосіб. Якщо кульовий сегмент менше за півкулю, то кульовий сегмент доповнюють конусом, у якого вершина знаходиться в центрі кулі, а основою є основа сегмента. Якщо ж сегмент більший від півкулі, то згаданий конус із нього вилучається (мал. 13). Об'єм кульового сектору одержуємо додаванням або відніманням об'ємів відповідних сегмента і конуса. Для об'єму кульового сектору маємо таку формулу:
Кульовим сектором називається тіло, одержане з кульового сегмента і конуса в такий спосіб. Якщо кульовий сегмент менше за півкулю, то кульовий сегмент доповнюють конусом, у якого вершина знаходиться в центрі кулі, а основою є основа сегмента. Якщо ж сегмент більший від півкулі, то згаданий конус із нього вилучається (мал. 13). Об'єм кульового сектору одержуємо додаванням або відніманням об'ємів відповідних сегмента і конуса. Для об'єму кульового сектору маємо таку формулу: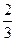
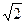 см. Обчислить об'єм циліндра.
см. Обчислить об'єм циліндра.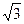 см. Знайдіть об'єм конуса.
см. Знайдіть об'єм конуса.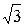 см і утворює з основою кут 30о. Обчислить об'єм циліндра.
см і утворює з основою кут 30о. Обчислить об'єм циліндра. см3, висота 2
см3, висота 2 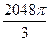 см3.
см3.


