
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Симетрія прямокутного паралелепіпедаСодержание книги
Поиск на нашем сайте
У прямокутного паралелепіпеда, як у будь-якого паралелепіпеда, є центр симетрії — точка перетинання його діагоналей. Він має також три площини симетрії, що проходять через центр симетрії паралельно граням. На малюнку 12 показано одну з таких площин. Вона проходить через середини чотирьох паралельних ребер паралелепіпеда. Кінці ребер є симетричними точками. Якщо у паралелепіпеда всі лінійні розміри різні, то він не має інших площин симетрії, крім названих. Якщо ж у паралелепіпеда два лінійні розміри однакові, то він має ще дві площини симетрії. Це площини діагональних перерізів, показані на малюнку 13. Якщо у паралелепіпеда всі лінійні розміри однакові, тобто він є кубом, то площина будь-якого його діагонального перерізу є площиною симетрії. Таким чином, куб має дев'ять площин симетрії.
Мал. 12 Мал. 13
Задачі до занять 1-2 1. Основа прямокутної призми – прямокутний трикутник з катетами 3 і 4 см, а висота призми 5 см. Знайти площу повної поверхні призми. 2. Бічне ребро похилої призми рівно 15 см і нахилене до площини основи під кутом 300. Знайти висоту призми. 3. Бічна поверхня правильної чотирикутної призми рівна 32 м2, а повна поверхня 40 м2. Знайти висоту. 4. У прямій трикутній призмі сторони основи рівні 10 см, 17см і 21 см, а висота призми 18 см. Знайти площу перерізу, проведеного через бічне ребро та меншу висоту основи. 5. У паралелепіпеда три грані мають площі 1 м2, 2 м2 і 3 м2. Чому дорівнює повна поверхня паралелепіпеда. 6. Знайти діагоналі прямокутного паралелепіпеда по трьом його вимірам: 1) 1,2,2; 2) 2,3,6; 3) 6,6,7. 7. В прямокутному паралелепіпеді сторони основи 7 дм і 24 дм, а висота паралелепіпеда 8 дм. Знайти площу діагонального перерізу. 8. Знайти поверхню прямокутного паралелепіпеда по трьом його вимірам: 10 см, 22 с, 16 см. 9. В прямокутному паралелепіпеді сторони основи 6 м і 8 м утворюють кут 300, бічне ребро рівне 5 м. Знайти повну поверхню цього паралелепіпеда. 10. В прямокутному паралелепіпеді сторони підстави 3 см мі 8 см, кут між ними 600. Бічна поверхня рівна 220 см2. Знайти повну поверхню.
Тема 3. Піраміда, її властивості. Правильна, зрізана піраміда. Площа бічної поверхні правильної піраміди. Властивості паралельних перерізів у піраміді
План
Відрізки, що сполучають вершину піраміди з вершинами
Поверхня піраміди складається з основи і бічних граней. Кожна бічна грань — трикутник. Однією з його вершин є вершина піраміди, а протилежною стороною - сторона основи піраміди. Висотою піраміди називається перпендикуляр, опущений з вершини піраміди на площину основи. Піраміда називається n -кутною, якщо її основою - n -кутною. Трикутна піраміда називається також тетраедром.
Мал. 14 У піраміди, зображеної на малюнку 14, основа - багатокутник А1А2... Аn,вершина піраміди — S, бічні ребра SA1, SА2,,..., SАп - бічні грані — ∆SA1A2, ∆S А2А3,.... Надалі будемо розглядати тільки піраміди з опуклим багатокутником в основі. Такі піраміди є опуклими многогранниками.
Відповідно до правил паралельного проектування піраміду зображують таким чином. Спочатку будують основу. Це — деякий плоский многокутник. Потім позначають вершину піраміди, яку з'єднують бічними ребрами з вершинами основи. На малюнку 14 зображена п’ятикутна піраміда. Перерізами піраміди площинами, які проходять через її вершину, є трикутники (мал. 15). Зокрема, трикутниками є діагональні перерізи. Це перерізи площинами, які проходять через два не сусідніх бічних ребра піраміди (мал. 16).
Мал.15 Мал. 16
Щоб побудувати переріз піраміди площиною, досить побудувати переріз її бічних граней із січною площиною. Якщо на грані, не паралельній сліду g (пряма, яка лежить у площині основи),відома яка-небудь точка А, щоналежить перерізу, то спочатку будують перетин сліду січної площини з площиною цієї грані — точку Dна малюнку 17. Точку D сполучають з точкою А прямою. Тоді відрізок цієї прямої, який належить грані, є перетином цієї грані із січною площиною. Якщо точка А лежить на грані, паралельній сліду g, то січна площина перетинає цю грань по відрізку, паралельному прямій g. Перейшовши до сусідньої бічної грані, будують її перетин із січною площиною і т.д. В результаті дістають шуканий переріз піраміди.
Мал. 17 Мал.18
На малюнку 18 побудовано переріз чотирикутної піраміди площиною, яка проходить через сторону основи і точку А на одному з її бічних ребер.
2. Піраміда називається правильною, якщо її основою є правильний многокутник, а основа висоти збігається з центром цього многокутника. Віссю правильної піраміди називається пряма, яка містить її висоту. Очевидно, у правильній піраміді бічні ребра рівні, отже, бічні грані — рівні рівнобедрені трикутники. Висота бічної грані правильної піраміди, проведена з її вершини, називається апофемою.
Теорема 5. Площину, яка перетинає піраміду і паралельна її основі, відтинає подібну піраміду.
Зрізана піраміда, яка отримана з правильної, також називається правильною. Бічні грані правильної зрізаної піраміди — рівні рівнобокі трапеції; їхні висоти називаються апофемами.
Мал.19 3. Бічною поверхнею піраміди називається сума площ її бічних граней. Теорема 6. Бічна поверхня правильної піраміди дорівнює добутку півпериметра основи на апофему. Доведення. Якщо сторона основи а, акількість сторін п, то бічна поверхня піраміди дорівнює:
де l — апофема, а р — периметр основи. Теорема доведена. Тема 4. Правильні многогранники
План: 1. Правильні многокутники 2. Розв’язування задач
Опуклий многогранник називається правильним, якщо його грані є правильними многокутниками з однією й тією самою кількістю сторін, а в кожній вершині многогранника сходиться одне і те ж число ребер. Існує п'ять типів правильних опуклих многогранників (мал. 20): правильний тетраедр, куб, октаедр, додекаедр, ікосаедр. У правильного тетраедра грані — правильні трикутники; у кожній вершині сходиться по три ребра. Тетраедр — трикутна піраміда, всі ребра якої рівні. У куба всі грані — квадрати; у кожній вершині сходиться по три ребра. Куб — прямокутний паралелепіпед з однаковими ребрами. У октаедра грані — правильні трикутники, але на відміну від тетраедра в кожній його вершині сходиться по чотири ребра. У додекаедра грані — правильні п'ятикутники. У кожній вершині його сходиться по три ребра. У ікосаедра грані — правильні трикутники, але на відміну від тетраедра і октаедра в кожній вершині сходиться по п'ять ребер.
Тетраедр Куб Октаедр Додекаедр Ікосаедр
Мал. 20
Задачі
Тема 5. Тіла обертання. Циліндр, осьовий переріз циліндра, площа бічної та повної поверхні циліндра
План
1. Циліндром (точніше, круговим циліндром) називається тіло, що складається з двох кругів, які не лежать в одній площині і суміщаються паралельним перенесенням, і всіх відрізків, що сполучають відповідні точки цих кругів (мал. 21). Круги називаються основами циліндра, а відрізки, що сполучають відповідні точки кіл кругів, - твірними циліндра.
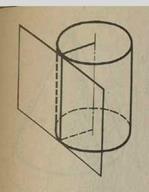
Мал.21 Мал.22 Оскільки паралельне перенесення — це рух, то основи циліндра рівні. Через те що при паралельному перенесенні площина переходить у паралельну площину (або в себе), та основи циліндра лежать у паралельних площинах. Оскільки при паралельному перенесенні точки зміщуються вздовж паралельних прямих або прямих, що збігаються, на одну й ту саму відстань, то твірні циліндра паралельні і рівні. Поверхня циліндра складається з основ і бічної поверхні. Бічна поверхня - з твірних. Циліндр називається прямим, якщо його твірні перпендикулярні до площин основ. Далі будемо розглядати тільки прямий циліндр, називаючи його коротко просто циліндром. Прямий циліндр наочно можна розглядати як тіло, утворене в результаті обертання прямокутника навколо сторони як осі (мал. 22). Радіусом циліндра називається радіус його основи. Висотою циліндра називається відстань між площинами його основ. Віссю циліндра називається пряма, що проходить через центри основ. Вона паралельна твірним. 2. Переріз циліндра площиною, паралельною його осі, є прямокутник (мал. 23). Дві його сторони — твірні циліндра, а дві інші — паралельні хорди основ. Зокрема, прямокутником є осьовий переріз. Це — переріз циліндра площиною, яка проходить через його вісь (мал. 24). Теорема 7. Площина, паралельна площини основи циліндра, перетинає його бічну поверхню по колу, яке дорівнює колу основи. Доведення. Нехай
Мал. 23 Мал.24 Мал. 25 Призмою, вписаною у циліндр, називається така призма, у якої площинами основ є площини основ циліндра, а бічними ребрами — твірні циліндра (мал. 26) Дотичною площиною до циліндра називається площина, яка проходить через твірну циліндра і перпендикулярна до площини осьового перерізу, що містить цю твірну (мал.27). Призмою, описаною навколо циліндра, називається призма, у якої площинами основ є площини основ циліндра, а бічні грані дотикаються до циліндра (мал. 28).
Мал. 26 Мал. 27 Мал. 28
Впишемо в циліндр правильну n-кутну призму (рис. 29). Площа бічної поверхні цієї призми Sп = РпН, де Рп — периметр основи призми, а Н - її висота. Як відомо, при необмеженому збільшенні п периметр Рп необмежено прямує до довжини С кола основи циліндра. Отже, площа бічної поверхні призми необмежено прямує до СН. Тому величину СН приймають за площу бічної поверхні циліндра.
Рис. 29 Мал.29
Sбок.п.цил. = СН = 2 де R — радіус циліндра, а Н — його висота.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 950; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.190.25.139 (0.009 с.) |



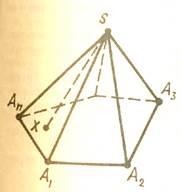 основи, називаються бічними ребрами.
основи, називаються бічними ребрами.
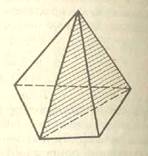


 Друга частина піраміди — це многогранник, який називається зрізаною пірамідою (мал. 19). Грані зрізаної піраміди, що лежать у паралельних площинах, називаються основами; інші грані називаються бічними гранями. Основи зрізаної піраміди є подібні (більше того, гомотетичні) многокутники, бічні грані — трапеції.
Друга частина піраміди — це многогранник, який називається зрізаною пірамідою (мал. 19). Грані зрізаної піраміди, що лежать у паралельних площинах, називаються основами; інші грані називаються бічними гранями. Основи зрізаної піраміди є подібні (більше того, гомотетичні) многокутники, бічні грані — трапеції. · n =
· n =  =
=  ,
,


 — площина, паралельна площини основи циліндра (мал. 25). Паралельне перенесення вздовж напрямку осі циліндра, яке суміщає площину
— площина, паралельна площини основи циліндра (мал. 25). Паралельне перенесення вздовж напрямку осі циліндра, яке суміщає площину 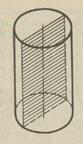




 3.Площа бічної і повної поверхні циліндра
3.Площа бічної і повної поверхні циліндра
 Таким чином, площа бічної поверхні циліндра обчислюється за формулою:
Таким чином, площа бічної поверхні циліндра обчислюється за формулою: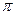 RН,
RН,


