
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Паралелепіпед, його властивості.Содержание книги
Поиск на нашем сайте
Паралелепіпед, його властивості.
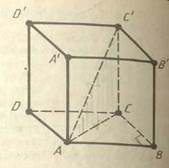
Якщо основою призми є паралелограм, то вона називається паралелепіпедом. У паралелепіпеда всі грані – паралелограми. На малюнку 8 а) зображено похилий паралелепіпед, а на малюнку 8 б) – прямий паралелепіпед.
Мал. 8
Грані паралелепіпеда, які не мають спільних вершин, називаються протилежними. Теорема 2. Протилежні грані паралелепіпеда паралельні і рівні.
З того, що грані паралелепіпеда — паралелограми, випливає, що відрізки А1А4, А'1А'4, А' 2 А'3 і А2А3 паралельні і рівні. Звідси робимо висновок, що грань А1А2А'2А'1 суміщається паралельним перенесенням вздовж ребра А1А4 із гранню АзА4А'4А'з. Отже, ці грані рівні. Аналогічно доводимо паралельність і рівність будь-яких двох протилежних граней паралелепіпеда. Мал. 9 Теорема доведена.
Т е о р е м а 3. Діагоналі паралелепіпеда перетинаються в одній точці і точкою перетину діляться пополам. Наслідок з теореми 3. Точка перетину діагоналей паралелепіпеда є його центром симетрії.
Мал. 10
Прямокутний паралелепіпед.
Прямий паралелепіпед, у якого основою є прямокутник, називається прямокутним паралелепіпедом. Усі грані прямокутного паралелепіпеда — прямокутники. Прямокутний паралелепіпед, у якого всі ребра рівні, називається кубом. Довжини непаралельних ребер прямокутного паралелепіпеда називаються його лінійними розмірами (вимірами). У прямокутного паралелепіпеда три лінійні виміри.
Теорема 4. У прямокутному паралелепіпеді квадрат будь-якої діагоналі дорівнює сумі квадратів трьох його вимірів.
Мал. 11 Задачі
Тема 5. Тіла обертання. Циліндр, осьовий переріз циліндра, площа бічної та повної поверхні циліндра
План
1. Циліндром (точніше, круговим циліндром) називається тіло, що складається з двох кругів, які не лежать в одній площині і суміщаються паралельним перенесенням, і всіх відрізків, що сполучають відповідні точки цих кругів (мал. 21). Круги називаються основами циліндра, а відрізки, що сполучають відповідні точки кіл кругів, - твірними циліндра.
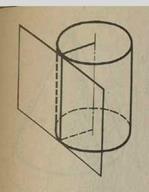
Мал.21 Мал.22 Оскільки паралельне перенесення — це рух, то основи циліндра рівні. Через те що при паралельному перенесенні площина переходить у паралельну площину (або в себе), та основи циліндра лежать у паралельних площинах. Оскільки при паралельному перенесенні точки зміщуються вздовж паралельних прямих або прямих, що збігаються, на одну й ту саму відстань, то твірні циліндра паралельні і рівні. Поверхня циліндра складається з основ і бічної поверхні. Бічна поверхня - з твірних. Циліндр називається прямим, якщо його твірні перпендикулярні до площин основ. Далі будемо розглядати тільки прямий циліндр, називаючи його коротко просто циліндром. Прямий циліндр наочно можна розглядати як тіло, утворене в результаті обертання прямокутника навколо сторони як осі (мал. 22). Радіусом циліндра називається радіус його основи. Висотою циліндра називається відстань між площинами його основ. Віссю циліндра називається пряма, що проходить через центри основ. Вона паралельна твірним. 2. Переріз циліндра площиною, паралельною його осі, є прямокутник (мал. 23). Дві його сторони — твірні циліндра, а дві інші — паралельні хорди основ. Зокрема, прямокутником є осьовий переріз. Це — переріз циліндра площиною, яка проходить через його вісь (мал. 24).
Теорема 7. Площина, паралельна площини основи циліндра, перетинає його бічну поверхню по колу, яке дорівнює колу основи. Доведення. Нехай
Мал. 23 Мал.24 Мал. 25 Призмою, вписаною у циліндр, називається така призма, у якої площинами основ є площини основ циліндра, а бічними ребрами — твірні циліндра (мал. 26) Дотичною площиною до циліндра називається площина, яка проходить через твірну циліндра і перпендикулярна до площини осьового перерізу, що містить цю твірну (мал.27). Призмою, описаною навколо циліндра, називається призма, у якої площинами основ є площини основ циліндра, а бічні грані дотикаються до циліндра (мал. 28).
Мал. 26 Мал. 27 Мал. 28
Впишемо в циліндр правильну n-кутну призму (рис. 29). Площа бічної поверхні цієї призми Sп = РпН, де Рп — периметр основи призми, а Н - її висота. Як відомо, при необмеженому збільшенні п периметр Рп необмежено прямує до довжини С кола основи циліндра. Отже, площа бічної поверхні призми необмежено прямує до СН. Тому величину СН приймають за площу бічної поверхні циліндра.
Рис. 29 Мал.29
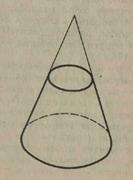
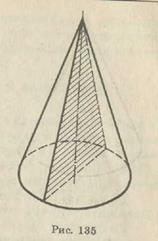
Sбок.п.цил. = СН = 2 де R — радіус циліндра, а Н — його висота. Переріз конуса площинами Переріз конуса площиною, яка проходить через його вершину, є рівнобедрений трикутник, у якого бічні сторони є твірними конуса (мал. 32). Зокрема, рівнобедреним трикутником є осьовий переріз конуса. Цей переріз, який проходить через вісь конуса (мал. 33). Теорема 8. Площина, паралельна площині основи конуса, перетинає конус по кругу, а бічну поверхню — по колу з центром на осі конуса. Доведення. Нехай
Мал.32 Мал.33 Мал.34
Площина, яка паралельна основі конуса і перетинає конус, відтинає від нього менший конус. Частина, що залишилася, називається зрізаним конусом (мал. 35).
Мал.35
ТІЛА ОБЕРТАННЯ
1. Радіус основи циліндра 2м, висота 3м. Знайдіть діагональ осьового перерізу. 2. Осьовий переріз циліндра – квадрат, площа якого Q. Знайдіть площу основи циліндра. 3. Висота циліндра 6см, радіус основи 5см. Знайдіть площу перерізу, проведеного паралельно осі циліндра на відстані 4см від неї. 4. Висота циліндра 8дм, радіус основи 5дм. Циліндр перетнуто площиною так, що в перерізі утворився квадрат. Знайдіть відстань від цього перерізу до осі. 5. Висота циліндра 6дм, радіус основи 5дм. Кінці відрізка АВ, який дорівнює 10дм лежать на колах обох основ. Знайдіть найкоротшу відстань від нього до осі.
6. Радіус основи конуса 3м, висота 4м. Знайдіть твірну. 7. Твірна конуса l нахилена до площини основи під кутом 30о. Знайдіть висоту. 8. Радіус основи конуса R. Осьовим перерізом конуса є прямокутний трикутник. Знайдіть його площу. 9. У рівносторонньому конусі (в осьовому перерізі – правильний трикутник) радіус основи R. Знайдіть площу перерізу, проведеного через дві твірні, кут між якими дорівнює α. 10. Висота конуса 20, радіус його основи 25. Знайдіть площу перерізу, проведеного через вершину, якщо відстань від нього до центру основи конуса дорівнює 12. 11. Радіуси основ зрізаного конуса 3м і 6м, висота 4м. Знайдіть твірну. 12. Радіуси основ зрізаного конуса R і r, твірна нахилена до основи під кутом 45о. Знайдіть висоту. 13. Твірна зрізаного конуса дорівнює 2 a і нахилена до основи під кутом 60о. Радіус однієї основи вдвічі більше радіуса іншої основи. Знайдіть радіуси. 14. Радіуси основ зрізаного конуса 3дм і 7дм, твірна 5дм. Знайдіть площу осьового перерізу. 15. Куля, радіус якої 41дм, перетнуто площиною на відстані 9дм від центра. Знайдіть площу перерізу. 16. Радіус кулі R. Через кінець радіуса проведена площина під кутом 60о до нього. Знайдіть площу перерізу. 17. Катети прямокутного трикутника дорівнюють 30см і 40см. На якій відстані від площини трикутника перебуває центр сфери, яка має радіус 65см, яка проходить через усі вершини трикутника. 18. Вершини прямокутника лежать на сфері радіусом 10см. Знайти відстань від центру сфери до площини прямокутника, якщо діагональ прямокутника рівна 16см. 19. На поверхні кулі дано 3 точки. Прямолінійні відрізки між даними точками дорівнюють 7см, 24см, 25см. 1) визначити вид трикутника, який виходить у результаті з'єднання відрізків; 2) знайдіть радіус перерізу кулі площиною даного трикутника; 3) знайдіть відстань від центру кулі до площини даного трикутника, якщо радіус кулі дорівнює 25см; 4) знайдіть довжину окружності перерізу поверхні кулі площиною даного трикутника; 5) знайдіть радіус окружності, вписаного у даний трикутник.
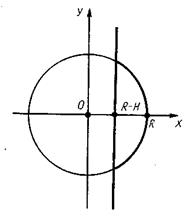
78. Мал.11 Кульовим сегментом називається частина кулі, що відтинається від нього площиною. Формулу для об'єму кульового сегмента одержують аналогічно формулі об'єму кулі (мал.12):
V = де R - радіус кулі, а Н — висота кульового сегмента.
Мал.12
V = де R - радіус кулі, Н - висота відповідного кульового сегмента.
Мал.13
Паралелепіпед, його властивості.
Якщо основою призми є паралелограм, то вона називається паралелепіпедом. У паралелепіпеда всі грані – паралелограми. На малюнку 8 а) зображено похилий паралелепіпед, а на малюнку 8 б) – прямий паралелепіпед.
Мал. 8
Грані паралелепіпеда, які не мають спільних вершин, називаються протилежними. Теорема 2. Протилежні грані паралелепіпеда паралельні і рівні.
З того, що грані паралелепіпеда — паралелограми, випливає, що відрізки А1А4, А'1А'4, А' 2 А'3 і А2А3 паралельні і рівні. Звідси робимо висновок, що грань А1А2А'2А'1 суміщається паралельним перенесенням вздовж ребра А1А4 із гранню АзА4А'4А'з. Отже, ці грані рівні. Аналогічно доводимо паралельність і рівність будь-яких двох протилежних граней паралелепіпеда. Мал. 9 Теорема доведена.
Т е о р е м а 3. Діагоналі паралелепіпеда перетинаються в одній точці і точкою перетину діляться пополам. Наслідок з теореми 3. Точка перетину діагоналей паралелепіпеда є його центром симетрії.
Мал. 10
Прямокутний паралелепіпед.
Прямий паралелепіпед, у якого основою є прямокутник, називається прямокутним паралелепіпедом. Усі грані прямокутного паралелепіпеда — прямокутники. Прямокутний паралелепіпед, у якого всі ребра рівні, називається кубом. Довжини непаралельних ребер прямокутного паралелепіпеда називаються його лінійними розмірами (вимірами). У прямокутного паралелепіпеда три лінійні виміри.
Теорема 4. У прямокутному паралелепіпеді квадрат будь-якої діагоналі дорівнює сумі квадратів трьох його вимірів.
Мал. 11
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 1530; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.176.111 (0.013 с.) |


 Доведення. Розглянемо які-небудь дві протилежні грані паралелепіпеда, наприклад А1А2А'2А'1 і Аза4А'4А'з (мал.9). Оскільки всі грані паралелепіпеда — паралелограми, то пряма А1А2 паралельна прямій А3А4, а пряма А1А'1 паралельна прямій А4А'4. Звідси випливає, що площини граней, які розглядаються, паралельні.
Доведення. Розглянемо які-небудь дві протилежні грані паралелепіпеда, наприклад А1А2А'2А'1 і Аза4А'4А'з (мал.9). Оскільки всі грані паралелепіпеда — паралелограми, то пряма А1А2 паралельна прямій А3А4, а пряма А1А'1 паралельна прямій А4А'4. Звідси випливає, що площини граней, які розглядаються, паралельні.


 — площина, паралельна площини основи циліндра (мал. 25). Паралельне перенесення вздовж напрямку осі циліндра, яке суміщає площину
— площина, паралельна площини основи циліндра (мал. 25). Паралельне перенесення вздовж напрямку осі циліндра, яке суміщає площину 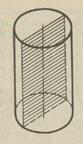




 3.Площа бічної і повної поверхні циліндра
3.Площа бічної і повної поверхні циліндра
 Таким чином, площа бічної поверхні циліндра обчислюється за формулою:
Таким чином, площа бічної поверхні циліндра обчислюється за формулою: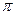 RН,
RН,


 Н),
Н),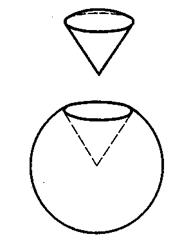 Кульовим сектором називається тіло, одержане з кульового сегмента і конуса в такий спосіб. Якщо кульовий сегмент менше за півкулю, то кульовий сегмент доповнюють конусом, у якого вершина знаходиться в центрі кулі, а основою є основа сегмента. Якщо ж сегмент більший від півкулі, то згаданий конус із нього вилучається (мал. 13). Об'єм кульового сектору одержуємо додаванням або відніманням об'ємів відповідних сегмента і конуса. Для об'єму кульового сектору маємо таку формулу:
Кульовим сектором називається тіло, одержане з кульового сегмента і конуса в такий спосіб. Якщо кульовий сегмент менше за півкулю, то кульовий сегмент доповнюють конусом, у якого вершина знаходиться в центрі кулі, а основою є основа сегмента. Якщо ж сегмент більший від півкулі, то згаданий конус із нього вилучається (мал. 13). Об'єм кульового сектору одержуємо додаванням або відніманням об'ємів відповідних сегмента і конуса. Для об'єму кульового сектору маємо таку формулу: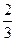
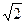 см. Обчислить об'єм циліндра.
см. Обчислить об'єм циліндра.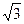 см. Знайдіть об'єм конуса.
см. Знайдіть об'єм конуса.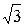 см і утворює з основою кут 30о. Обчислить об'єм циліндра.
см і утворює з основою кут 30о. Обчислить об'єм циліндра. см3, висота 2
см3, висота 2 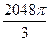 см3.
см3.


