

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Релаксация для различных материалов
Таблица VIII‑34
| Материал
| Объект испытания
|  , Н/мм2 , Н/мм2
| Начальное напряжение, Н/мм2
| Температура, 
| Время, час
| Релаксация, %
| | GD-Zn Al1 Cu 1
| Резьба
|
|
|
|
|
| | GD-Mg Al8 Zn 1
GD-Al Si12 (Cu)
| Испытания на сжатие
|
|
|
|
|
3,3
| | Cq35
| Винт
|
|
|
|
|
| | 40Cr Mo V 47
| Образец для испытания на растяжение
|
|
|
|
|
|
7.2.14. Коэффициент концентрации напряжений  для различных видов надрезов для различных видов надрезов
Значение коэффициент концентрации для плоских стержней
Значение коэффициент концентрации для круглых стержней
Моменты сопротивления и моменты инерции площади сечения
NL – «нейтральная ось»
Таблица VIII‑35
| Форма сечения
| Момент сопротивления
 при изгибе при изгибе
 при кручении при кручении
| Момент инерции для площадей
 - осевой, относительно NL, - осевой, относительно NL,
 - полярный, относительно центра тяжести - полярный, относительно центра тяжести
|

| 

| 

|

| 

| 

|

| 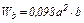

| 

| при 
|

| 

| 

|

| 

| 
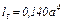
|

| 

| 

| | В случае кручения исходная площадь поперечного сечения не сохраняется
|

| 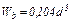

| 

|

| 

| 

|

| 
| 
|

| 
| 
|

| 
| 
|
Раздел.8. Математика
Математические знаки и символы
| ≈
| приблизительно равно
|
| ...
| и т.д.
| 
| значительно меньше
|
| n!
| n факториал т.е. (3!=1*2*3=6)
| 
| значительно больше
|
| 
| абсолютная величина x
| 
| соответствует
|
| 
| стремиться
| | =
| равно
|
| ∞
| бесконечность
| | ≠
| неравно
|
| i или j
| мнимое число, i2 = -1
| | <
| меньше
|
|  
| перпендикулярно
| | ≤
| меньше или равно
|
| ||
| параллельно
| | >
| больше
|
| 
| угол
| | ≥
| больше или равно
|
| ∆
| треугольник
| | +
| плюс (сложение)
|
| lim
| предел
| | -
| минус (вычитание)
|
| Δ
| дельта (разность между двумя величинами)
| 
| умножение
|
| d
| полный дифференциал
| 
| деление
|
| δ
| частный дифференциал
| | ∑
| суммирование
|
| 
| интеграл
| | П
| произведение
|
| ln
| логарифм по основанию e *)
(или натуральный логарифм)
| | ~
| пропорционально
|
| lg
| логарифм по основанию 10
(или десятичный логарифм)
| 
| корень
|
| logab
| логарифм числаb по основанию a
| 
| корень n-ой степени
|
|
|
|
Полезные числовые значения
| е
| =
| 2,718282*
| lg e
| =
| 0,367879
| lg 10
| =
| 2,302585
| 
| =
| 1,77245
| 180/ π
| =
| 57,29578
| 
| =
| 0,70711
| | e2
| =
| 7,389056
| 
| =
| 1,648721
| 1/ lg 10
| =
| 0,434294
| 1/ π
| =
| 0,31831
| π/180
| =
| 0,017453
| 
| =
| 1,73205
| | 1/e
| =
| 0,367879
| 1/ lg e
| =
| 2,302585
| π
| =
| 3,14159
| π 2
| =
| 9,86960
| 
| =
| 1,41421
| |
|
|
Системы чисел
Общие сведения
Системы чисел используются для образования записей чисел в случаях, когда число цифр должно быть меньше количеству подлежащих описанию отдельных единиц. Этот тип обозначения требует использования единичного символа (цифры) для коллективного представления более одного элемента.
Сегодняшнее стандартное описание или система счисления, отличается от аддитивных систем, например римской. Положение цифры при записи числа соответствует размеру единицы (разрядное значение). Число, при котором формируется первая новая единица, является базовым числом системы счисления; оно равняется максимальному числу отдельных цифр, которые имеются в распоряжении.
Наиболее часто используются десятичные системы счисления (с основанием 10). Двоичная система счисления (с основанием 2), в которой используются цифры 1 и 0. И шеснадцатиричная (с основанием 16), с использованием цифр от 0 до 9 и букв от A до F, которая довольно часто применяются для обработки данных.
Действительное число a в разрядной системе представляется как:  , ,
где i - позиция; B – основание; Zi – натуральное число (0≤ Zi <B) в позиции i.
| Римская система счисления аддитивная
| I
| X
| C
| M
| II
| V
| L
| D
| MVM
| | Десятичная система (основание 10)
|
|
|
|
|
|
|
|
|
| | Двоичная система (основание 2)
|
|
|
|
|
|
|
|
|
|
Предпочтительные числа
Предпочтительные числа являются округленными членами геометрического ряда, имеющими следующие знаменатели (отношение последующего члена к предыдущему):
| Ряд
| R5
| R10
| R20
| R40
| | Знаменатель
| 
| 
| 
| 
| Ряды используются для выбора предпочтительного размера и значения знаменателей. Электрические компоненты, например резисторы и конденсаторы, ранжируются в зависимости от знаменателей в соответствии с Е-рядом:
| Ряд
| E6
| E12
| E24
| | Знаменатель
| 
| 
| 
|
| Предпочтительные числа
| Е – ряд
| | Основной ряд
| Точные значения
| lg
|
|
|
|
|
|
| | R5
| R10
| R20
|
|
|
|
|
|
| | 1,00
| 1,00
| 1,00
| 1,00
| 1,0000
| 0,0
|
| Е6
| Е12
| Е24
|
|
| |
|
|
| 1,06
| 1,0593
| 0,025
|
| 1,0
| 1,0
| 1,0
|
|
| |
|
| 1,12
| 1,12
| 1,1220
| 0,05
|
|
|
| 1,1
|
|
| |
|
|
| 1,18
| 1,1885
| 0,075
|
|
| 1,2
| 1,2
|
|
| |
| 1,25
| 1,25
| 1,25
| 1,2589
| 0,1
|
|
|
| 1,3
|
|
| |
|
|
| 1,32
| 1,3335
| 0,125
|
| 1,5
| 1,5
| 1,5
|
|
| |
|
| 1,40
| 1,40
| 1,4125
| 0,15
|
|
|
| 1,6
|
|
| |
|
|
| 1,50
| 1,4962
| 0,175
|
|
| 1,8
| 1,8
|
|
| | 1,60
| 1,60
| 1,60
| 1,60
| 1,5849
| 0,2
|
|
|
| 2,0
|
|
| |
|
|
| 1,70
| 1,6788
| 0,225
|
| 2,2
| 2,2
| 2,2
|
|
| |
|
| 1,80
| 1,80
| 1,7783
| 0,25
|
|
|
| 2,4
|
|
| |
|
|
| 1,90
| 1,8836
| 0,275
|
|
| 2,7
| 2,7
|
|
| |
| 2,00
| 2,00
| 2,00
| 1,9953
| 0,3
|
|
|
| 3,0
|
|
| |
|
|
| 2,12
| 2,1135
| 0,325
|
| 3,3
| 3,3
| 3,3
|
|
| |
|
| 2,24
| 2,24
| 2,2387
| 0,35
|
|
|
| 3,6
|
|
| |
|
|
| 2,36
| 2,3714
| 0,375
|
|
| 3,9
| 3,9
|
|
| | 2,50
| 2,50
| 2,50
| 2,50
| 2,5119
| 0,4
|
|
|
| 4,3
|
|
| |
|
|
| 2,65
| 2,6607
| 0,425
|
| 4,7
| 4,7
| 4,7
|
|
| |
|
| 2,80
| 2,80
| 2,8184
| 0,45
|
|
|
| 5,1
|
|
| |
|
|
| 3,00
| 2,9854
| 0,475
|
|
| 5,6
| 5,6
|
|
| |
| 3,15
| 3,15
| 3,15
| 3,1623
| 0,5
|
|
|
| 6,2
|
|
| |
|
|
| 3,35
| 3,3497
| 0,525
|
| 6,8
| 6,8
| 6,8
|
|
| |
|
| 3,55
| 3,55
| 3,5481
| 0,55
|
|
|
| 7,5
|
|
| |
|
|
| 3,75
| 3,7584
| 0,575
|
|
| 8,2
| 8,2
|
|
| | 4,00
| 4,00
| 4,00
| 4,00
| 3,9811
| 0,6
|
|
|
| 9,1
|
|
| |
|
|
| 4,25
| 4,2170
| 0,625
|
| 10,0
| 10,0
| 10,0
|
|
| |
|
| 4,50
| 4,50
| 4,4668
| 0,65
|
|
|
|
|
|
| |
|
|
| 4,75
| 4,7315
| 0,675
|
|
|
|
|
|
| |
| 5,00
| 5,00
| 5,00
| 5,0119
| 0,7
|
|
|
|
|
|
| |
|
|
| 5,30
| 5,3088
| 0,725
|
|
|
|
|
|
| |
|
| 5,60
| 5,60
| 5,6234
| 0,75
|
|
|
|
|
|
| |
|
|
| 6,00
| 5,9566
| 0,775
|
|
|
|
|
|
| | 6,30
| 6,30
| 6,30
| 6,30
| 6,3096
| 0,8
|
|
|
|
|
|
| |
|
|
| 6,70
| 6,6834
| 0,825
|
|
|
|
|
|
| |
|
| 7,10
| 7,10
| 7,0795
| 0,85
|
|
|
|
|
|
| |
|
|
| 7,50
| 7,4989
| 0,875
|
|
|
|
|
|
| |
| 8,00
| 8,00
| 8,00
| 7,9433
| 0,9
|
|
|
|
|
|
| |
|
|
| 8,50
| 8,4140
| 0,925
|
|
|
|
|
|
| |
|
| 9,00
| 9,00
| 8,9125
| 0,95
|
|
|
|
|
|
| |
|
|
| 9,50
| 9,4409
| 0,975
|
|
|
|
|
|
| | 10,0
| 10,0
| 10,0
| 10,0
| 10,0000
| 1,0
|
|
|
|
|
|
|
Тригонометрические функции
Определения

|
| φ =
| ± α
| 90 ± α
| 180 ± α
| 270 ± α
| |
| sin φ =
| ± sin α
| cos α
|  sin α sin α
| - cos α
| |
| cos φ =
| + cos α
|  sin α sin α
| - cos α
| ± sin α
| |
| tg φ =
| ± tg α
|  ctg α ctg α
|  tg α tg α
|  ctg α ctg α
| |
| cos φ =
| ± ctg α
|  tg α tg α
|  ctg α ctg α
|  tg α tg α
| |
| | |
| Синус α = sin α = отношение катета, противолежащего углу α, к гипотенузе.
| |
| Косинус α = cos α = отношение катета, прилежащего углу α, к гипотенузе.
| |
| Тангенс α = tg α = отношение катета противолежащего, углу α, к катету, прилежащего углу α.
| |
| Котангенс α = ctg α = отношение катета, прилежащего углу α, к катету, противолежащего углу α.
| |
| Дата угла  - радианной мере угла α для круга, радиус которого равен 1. - радианной мере угла α для круга, радиус которого равен 1.
| | sin 0 ° = cos 90 ° = 0
|
| 
| | cos 0 ° = sin 90 ° = 1
|
| 
| | tg 0 ° = ctg 90 ° = 1
|
| 
| | ctg 0 ° = tg 90 ° = ∞
|
| 
| | sin 30 ° = cos 60 °О = 0,5
|
| 
| cos 30 ° = sin 60 ° = 
|
| 
| tg 30 ° = ctg 60 ° = 
|
| 
| ctg 30 ° = tg 60 ° = 
|
| 
| 
|
| 
| 
|
| 
| | arc 57,3 ° = 1
|
| 
| | cos2α + sin 2α = 1
|
| 
| 
|
| 
| 
|
| 
| 
|
| 
|  ошибка < 1% при α < 58 ° ошибка < 1% при α < 58 °
|
| Уравнение Эйлера
(Основа символического метода)
|  ошибка < 1% при α < 14 ° ошибка < 1% при α < 14 °
|
| 
|  ошибка < 1% при α < 37 ° ошибка < 1% при α < 37 °
|
|  ; ; 
| | cos α = 1 ошибка < 1% при α < 8 °
|
| при 
|
Таблица перевода тригонометрических функций
| α
| arc α, рад
| sin α
| tg α
| ctg α
| inv α*
| cos α
| -
| -
| |
| 0,0000
| 0,0000
| 0,0000
| ∞
| 0,0000
| 1,0000
| 1,5707
|
| |
| 0,0175
| 0,0175
| 0,0175
| 57,290
| 0,0000
| 0,9998
| 1,5532
|
| |
| 0,0349
| 0,0349
| 0,0349
| 28,636
| 0,0000
| 0,9994
| 1,5358
|
| |
| 0,0524
| 0,0523
| 0,0524
| 19,081
| 0,0001
| 0,9986
| 1,5183
|
| |
| 0,0698
| 0,0698
| 0,0699
| 14,301
| 0,0001
| 0,9976
| 1,5009
|
| |
| 0,0873
| 0,0872
| 0,0875
| 11,430
| 0,0002
| 0,9962
| 1,4834
|
| |
| 0,1047
| 0,1045
| 0,1051
| 9,5144
| 0,0004
| 0,9945
| 1,4660
|
| |
| 0,1222
| 0,1219
| 0,1228
| 8,1443
| 0,0006
| 0,9925
| 1,4485
|
| |
| 0,1396
| 0,1392
| 0,1405
| 7,1154
| 0,0009
| 0,9903
| 1,4311
|
| |
| 0,1571
| 0,1564
| 0,1584
| 6,3138
| 0,0013
| 0,9877
| 1,4136
|
| |
| 0,1745
| 0,1736
| 0,1763
| 5,6713
| 0,0018
| 0,9848
| 1,3962
|
| |
| 0,1920
| 0,1908
| 0,1944
| 5,1446
| 0,0024
| 0,9816
| 1,3787
|
| |
| 0,2094
| 0,2079
| 0,2126
| 4,7046
| 0,0031
| 0,9781
| 1,3613
|
| |
| 0,2269
| 0,2250
| 0,2309
| 4,3315
| 0,0040
| 0,9744
| 1,3438
|
| |
| 0,2443
| 0,2419
| 0,2493
| 4,0108
| 0,0050
| 0,9703
| 1,3264
|
| |
| 0,2618
| 0,2588
| 0,2679
| 3,7321
| 0,0062
| 0,9659
| 1,3089
|
| |
| 0,2792
| 0,2756
| 0,2867
| 3,4874
| 0,0075
| 0,9613
| 1,2914
|
| |
| 0,2967
| 0,2924
| 0,3057
| 3,2709
| 0,0090
| 0,9563
| 1,2740
|
| |
| 0,3141
| 0,3090
| 0,3249
| 3,0777
| 0,0108
| 0,9511
| 1,2565
|
| |
| 0,3316
| 0,3256
| 0,3443
| 2,9042
| 0,0127
| 0,9455
| 1,2391
|
| |
| 0,3490
| 0,3420
| 0,3640
| 2,7475
| 0,0149
| 0,9397
| 1,2216
|
| |
| 0,3665
| 0,3584
| 0,3839
| 2,6051
| 0,0174
| 0,9336
| 1,2042
|
| |
| 0,3839
| 0,3746
| 0,4040
| 2,4751
| 0,0201
| 0,9272
| 1,1867
|
| |
| 0,4014
| 0,3907
| 0,4245
| 2,3559
| 0,0231
| 0,9205
| 1,1693
|
| |
| 0,4188
| 0,4067
| 0,4452
| 2,2460
| 0,0264
| 0,9135
| 1,1518
|
| |
| 0,4363
| 0,4226
| 0,4663
| 2,1445
| 0,0300
| 0,9063
| 1,1344
|
| |
| 0,4538
| 0,4384
| 0,4877
| 2,0503
| 0,0340
| 0,8988
| 1,1169
|
| |
| 0,4712
| 0,4540
| 0,5095
| 1,9626
| 0,0383
| 0,8910
| 1,0995
|
| |
| 0,4887
| 0,4695
| 0,5317
| 1,8807
| 0,0431
| 0,8829
| 1,0820
|
| |
| 0,5061
| 0,4848
| 0,5543
| 1,8040
| 0,0482
| 0,8746
| 1,0646
|
| |
| 0,5236
| 0,5000
| 0,5774
| 1,7321
| 0,0538
| 0,8660
| 1,0471
|
| |
| 0,5410
| 0,5150
| 0,6009
| 1,6643
| 0,0598
| 0,8572
| 1,0297
|
| |
| 0,5585
| 0,5299
| 0,6249
| 1,6003
| 0,0664
| 0,8480
| 1,0122
|
| |
| 0,5759
| 0,5446
| 0,6494
| 1,5399
| 0,0735
| 0,8387
| 0,9948
|
| |
| 0,5934
| 0,5592
| 0,6745
| 1,4826
| 0,0811
| 0,8290
| 0,9773
|
| |
| 0,6108
| 0,5736
| 0,7002
| 1,4281
| 0,0894
| 0,8192
| 0,9599
|
| |
| 0,6283
| 0,5878
| 0,7265
| 1,3764
| 0,0983
| 0,8090
| 0,9424
|
| |
| 0,6457
| 0,6018
| 0,7536
| 1,3270
| 0,1078
| 0,7986
| 0,9250
|
| |
| 0,6632
| 0,6157
| 0,7813
| 1,2799
| 0,1181
| 0,7880
| 0,9075
|
| |
| 0,6806
| 0,6293
| 0,8098
| 1,2349
| 0,1292
| 0,7771
| 0,8901
|
| |
| 0,6981
| 0,6428
| 0,8391
| 1,1918
| 0,1410
| 0,7660
| 0,8726
|
| |
| 0,7155
| 0,6561
| 0,8693
| 1,1504
| 0,1538
| 0,7547
| 0,8551
|
| |
| 0,7330
| 0,6691
| 0,9004
| 1,1106
| 0,1674
| 0,7431
| 0,8377
|
| |
| 0,7504
| 0,6820
| 0,9325
| 1,0724
| 0,1821
| 0,7314
| 0,8202
|
| |
| 0,7679
| 0,6947
| 0,9657
| 1,0355
| 0,1978
| 0,7193
| 0,8028
|
| |
| 0,7853
| 0,0000
| 1,0000
| 1,0000
| 0,2147
| 0,7071
| 0,7853
|
| | -
| -
| cos α
| ctg α
| tg α
| -
| sin α
| arc α, рад
| α
|
|



 , Н/мм2
, Н/мм2

 для различных видов надрезов
для различных видов надрезов

 при изгибе
при изгибе
 при кручении
при кручении
 - осевой, относительно NL,
- осевой, относительно NL,
 - полярный, относительно центра тяжести
- полярный, относительно центра тяжести











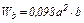













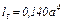






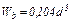
































 ,
,







 sin α
sin α
 - радианной мере угла α для круга, радиус которого равен 1.
- радианной мере угла α для круга, радиус которого равен 1.






















 ошибка < 1% при α < 58 °
ошибка < 1% при α < 58 °
 ошибка < 1% при α < 14 °
ошибка < 1% при α < 14 °

 ошибка < 1% при α < 37 °
ошибка < 1% при α < 37 °
 ;
; 




