Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод эквивалентного генератора.Содержание книги
Поиск на нашем сайте
В соответствие с т Тевенина и Нортона задающее напряжение генератора определяется как напряжение хх на разомкнутых зажимах активного 2-х-полюсника Uг=Uхх, а задающий ток- как ток кз Iг=Iкз. внутреннее R активного 2-х-полюсника или его проводимость Gг находятся как эквивалентные входные сопротивления или проводимость отн-но разомкнутых зажимов пассивного 2-х-полюсника, к-ый получается после исключения из схемы всех источников напряжения и тока. При этом идеальные источники напряжения закорачиваются, а токи- размыкаются; реальные источники заменяются своими внутренними сопротивлениями или проводимостями.
Баланс мощности. Сумма мощности, вырабатываемая независимым источником = сумме мощностей, потребляемыми всеми эл-тами эл цепи
Расчет электрической цепи с зависимыми источниками. Для расчета цепей, содержащихзависимые источники, применимы все методы, известные для расчета цепей с независимыми источниками. Наиболее часто используются методы узловых напряжений и контурных токов.
Рисунок 4.6 Рисунок 4.7 Пример 1. В цепи (рисунок 4.6) действуют независимый источник тока J и ИНУТ с ЭДС Е =rI2. Дано: R1, R2, r, J. Найти напряжение Uab. Решение. Выберем для решения метод контурных токов. Контурное уравнение: I11 (R1+R2)+J R2=E.Учитывая, что I2=I11+J, I11 (R1+R2)+J R2=r(I11+J) или I11(R1+R2 - r)= J (r - R2). Из этого уравнения определим ток I11. Напряжение Uab = I2 R2. Пример 2. В цепи (рис.4.7) действуют независимые источник напряжения с ЭДС E1 и ИНУН с ЭДС E2=k Uab. Найти токи в ветвях, если даны R1,R2,R3, k. Решение. Для решения выберем метод узловых потенциалов. Приняв φb = 0, запишем уравнение для узла α φα (1 / R1+1 / R2+1 / R3) = E1 / R1+E2 / R2. Учитывая, что Uab = φa-φb, E2=kφа имеем φα (1 / R1+1 / R2+1 / R3) = E1 / R1+ kφа / R2. Решая уравнение, получим φa= Uab. Токи в ветвях I1= (Uab+E1)/ R1; I2=(Uab- E2) / R2, I3= Uab / R3. Гармонические токи, напряжения, ЭДС. Электромагнитный процесс в ЭЦ, при котором мгновенные значения напряжения и токов повторяются через равные промежутки времени, называются периодическим. Периодический процесс называется гармоническим, если функция f(t) (напряжение, ЭДС, ток) изменяется по закону синуса
f(t) = Am sin(wt +j); (3.1) u = Um sin(wt +jU); e = Em sin(wt + je); i = Im sin(wt = ji)
Значения u, e, i, в любой момент времени называются мгновенными значениями.
Наибольшее по абсолютному значению отклонение колеблющейся величины называется ее амплитудой Наименьшее значение времени, после которого процесс полностью повторяется, называется периодом колебания Т. Число циклов колебаний в единицу времени называется циклической частотой Число циклов колебаний в интервале времени равному 2p единицам, называется угловой частотой Величина
Способы представления гармонических колебаний. Гармонич. колебания можно представить: фун-ей времени (временные диаграммы), вращающимися векторами (векторные диаграммы), комплексныеми числами; амплитудными и фазовыми спектрами Временные диаграммы - громоздкие тригонометрич выражения. Совокупность векторов, изображающих гармонические колебания в эл цепи, наз векторной диаграммой. Их можно строить как для амплитудных, так и дл ядействующих значений токов и напряжений. Каждому колебанию ставится вращающий вектор определенной длины с заданной нач фазой.
Метод комплексных амплитуд: ток i из
Спектральное (частотное) представление гармонических колебаний состоит в задании амплитудного и фазового спектров колебаний.
|
||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 304; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.19.240.129 (0.008 с.) |

 или
или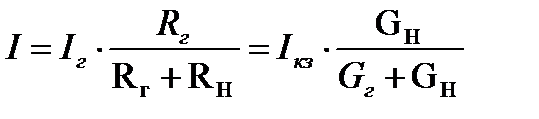
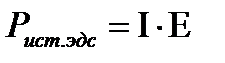
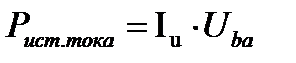



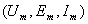 .
. .
. .
.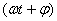 называется фазой колебания. Она характеризует состояние колебания в любой момент времени t.
называется фазой колебания. Она характеризует состояние колебания в любой момент времени t. Значение фазы колебания в момент времени t=0 называется начальной фазой
Значение фазы колебания в момент времени t=0 называется начальной фазой 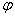 . Начальная фаза является алгебраической величиной. При
. Начальная фаза является алгебраической величиной. При  начало синусоиды сдвинуто влево, а при
начало синусоиды сдвинуто влево, а при 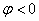 - вправо от начала координат.
- вправо от начала координат.
 можно представить как геометрическую разность векторов Im/2 и Im*/2, вращающихся в пртивоположных направлениях с угловой частотой
можно представить как геометрическую разность векторов Im/2 и Im*/2, вращающихся в пртивоположных направлениях с угловой частотой  , а ток из
, а ток из  - как геометрическую сумму этих векторов. В первом случае I располагается на мнимой, а во втором случае – на действительной осях.
- как геометрическую сумму этих векторов. В первом случае I располагается на мнимой, а во втором случае – на действительной осях.