Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Частотные характеристики последовательного контура.Содержание книги
Поиск на нашем сайте
При
Резонанс токов. Резонанс – состояние эл цепи, состоящей из разнохарактерных эл-ов, при к-ой фазовый сдвиг м/у входным током и приложенным напряжением равен нулю Возникает в параллельном контуре. Резонанс наступает если у входной проводим-ти
Где Резонансная частота Резонанс возможен, если сопротивление r1 и r2 оба больше или оба меньше При r1= r2 При
Частотные характеристики параллельного контура.
резонанс в параллельном контуре возможен: если сопротивление R1 и R2 оба больше или оба меньше Периодические несинусоидальные воздействия. На практике э.д.с., напряжения и токи в большей или меньшей степени являются несинусоидальными. Это связано с тем, что реальные генераторы не обеспечивают, строго говоря, синусоидальной формы кривых напряжения, а с другой стороны, наличие нелинейных элементов в цепи обусловливает искажение формы токов даже при синусоидальных ЭДС источников. В радиотехнике, вычислительной технике и т.п. применяются генераторы периодических несинусоидальных импульсов. В общем случае характер изменения несинусоидальных величин может быть периодическим, почти периодическим и непериодическим. В данной лекции будут рассматриваться цепи только с несинусоидальными периодическими э.д.с., напряжениями и токами. В качестве примера (рисунок 13.1,а) представлена цепь с нелинейным резистором (НР), нелинейная вольт-амперная характеристика (ВАХ) которого обусловливает несинусоидальную форму тока i в цепи при синусоидальном напряжении u на ее входе (рисунок 13.1,б).
Рисунок 13.1
Расчет цепей при периодических несинусоидальных воздействиях. Расчёт линейных электрических цепей несинусоидального тока распадается на три этапа:
а) разложение несинусоидальных э.д.с. и токов источников на постоянную и синусоидальные составляющие (т.е. в тригонометрический ряд Фурье); б) применение принципа наложения и расчет токов и напряжений в цепи для каждой из составляющих в отдельности. При расчете цепи с постоянными составляющими э.д.с. и тока источника следует учитывать, что индуктивное сопротивление равно 0 и индуктивность в эквивалентной схеме заменяется короткозамкнутым участком, а ёмкостное равно в) совместное рассмотрение решений, полученных для каждой из составляющих. Причём суммируются только мгновенные значения составляющих токов и напряжений.
Общие положения и классификация четырехполюсников. Четырёхполюсником называется электрическая цепь или её часть, имеющая две пары зажимов (полюсов), для подключения к источнику и приемнику электрической энергии. К четырёхполюсникам относятся трансформаторы, усилители, электрические фильтры, линии передачи электрической энергии и т.д. Таким образом, теория четырёхполюсников позволяет едиными методами анализировать системы различные по структуре и принципу действия. Условное изображения четырёхполюсников показано на рисунке 14.1.
Рисунок 14.1 Пара зажимов Активные и пассивные четырехполюсники. Активные четырехполюсники содержат независимые и зависимые источники, пассивные четырехполюсники не содержат источников электрической энергии. Линейные и нелинейные четырёхполюсники.
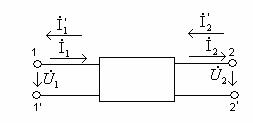
Линейные четырёхполюсники не содержат нелинейные элементы, нелинейные четырёхполюсники содержат нелинейные элементы. Обратимые и необратимые четырёхполюсники. Для обратимых четырёхполюсников выполняется теорема обратимости или взаимности: отношение напряжения на входе к току на выходе не меняется при перемене местами зажимов. Пассивные четырёхполюсники всегда обратимы. Симметричные и несимметричные четырёхполюсники. В симметричном четырёхполюснике перемена местами входных и выходных зажимов не изменяет напряжений и токов в цепи. Схемы типовых пассивных четырёхполюсников показаны на рисунках 14.2 а), 14.2 б), 14.2 в),14.2 г).
Рисунок 14.2
|
||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 313; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.79.212 (0.008 с.) |







 цепь имеет резистивно-емкостной х-р (X<0
цепь имеет резистивно-емкостной х-р (X<0  ) и ток опережает по фазе приложенное напряжение, при
) и ток опережает по фазе приложенное напряжение, при  х-р цепи резистивно-индуктивный (Х>0
х-р цепи резистивно-индуктивный (Х>0  ) и ток отстает по фазе от приложенного напряжения, при
) и ток отстает по фазе от приложенного напряжения, при  наступает резонанс напряжений (Х=0
наступает резонанс напряжений (Х=0  ) и ток совпадает по фазе с приложенным напряжением
) и ток совпадает по фазе с приложенным напряжением


 , реактивная состовляющая
, реактивная состовляющая  или
или 
 и
и  - реактивные провод-ти ветвей
- реактивные провод-ти ветвей
 .
.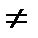
 резонансная частота имеет любое значение, т.е. резонанс наблюдается на любой частоте.
резонансная частота имеет любое значение, т.е. резонанс наблюдается на любой частоте.










 - при резонансе
- при резонансе



 и ветвь с ёмкостью размыкается. При расчете цепи для каждой синусоидальной составляющей э.д.с. и тока источника можно пользоваться комплексным методом, но недопустимо сложение комплексных токов и напряжений различных синусоидальных составляющих. Необходимо учитывать, что индуктивное и емкостное сопротивления для различных частот неодинаковы, индуктивное сопротивление для k-й гармоники равно:
и ветвь с ёмкостью размыкается. При расчете цепи для каждой синусоидальной составляющей э.д.с. и тока источника можно пользоваться комплексным методом, но недопустимо сложение комплексных токов и напряжений различных синусоидальных составляющих. Необходимо учитывать, что индуктивное и емкостное сопротивления для различных частот неодинаковы, индуктивное сопротивление для k-й гармоники равно:  , а емкостное сопротивление для k-й гармоники равно:
, а емкостное сопротивление для k-й гармоники равно:  ;
;
 называются первичными,
называются первичными,  называются вторичными, зажимы, к которым подключается источник называются входными, зажимы, к которым подключается приёмник называются выходными. Положительные направления напряжений и токов показано на рисунке 14.1.
называются вторичными, зажимы, к которым подключается источник называются входными, зажимы, к которым подключается приёмник называются выходными. Положительные направления напряжений и токов показано на рисунке 14.1.