
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сила давления жидкости на криволинейную стенкуСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Чаще всего необходимо определить силу, действующую на цилиндрическую поверхность, имеющую вертикальную ось симметрии. Возможны два варианта. Первый вариант - жидкость воздействует на стенку изнутри. Во втором варианте жидкость действует на стенку снаружи. Рассмотрим оба этих варианта.
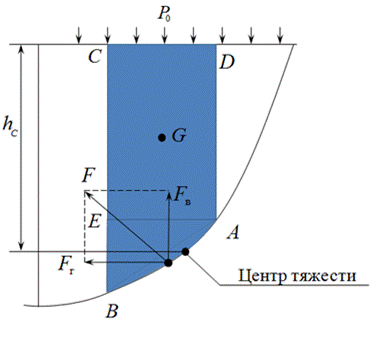
Рисунок 4.2 Действие жидкости на цилиндрическую стенку изнутри В первом случае выделим объём жидкости, ограниченный рассматриваемым участком цилиндрической поверхности AB, участком свободной поверхности CD, расположенным над участком AB, и двумя вертикальными поверхностями BC и АD, проходящими через точки A и B. Эти поверхности ограничивают объём ABCD, который находится в равновесии. Рассмотрим условия равновесия этого объёма в вертикальном и горизонтальном направлениях. Если жидкость действует на поверхность AB, c какой-то силой F, то с такой же силой, но в обратном направлении, и поверхность действует на рассматриваемый объём жидкости. Эту силу, перпендикулярную поверхности AB, можно представить в виде горизонтальной F г и вертикальной F в составляющих. Условие равновесия объёма ABCD в вертикальном направлении:
где
Условие равновесия этого объёма в горизонтальной плоскости запишем с учётом того, что силы, действующие на одинаковые вертикальные поверхности AD и CE, взаимно уравновешиваются. Остаётся только сила давления на площадь BE, которая пропорциональна вертикальной проекции S в поверхности AB. С учётом частичного уравновешивания будем иметь условие равновесия сил в горизонтальном направлении в виде:
где Зная
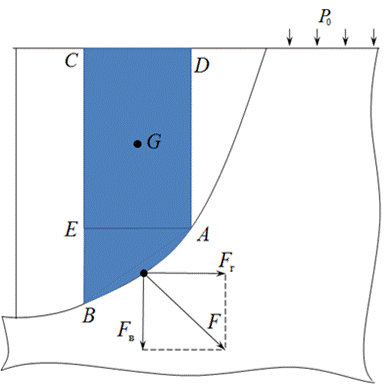
Рисунок 4.3 Действие жидкости на цилиндрическую стенку снаружи Во втором случае, когда жидкость воздействует на цилиндрическую поверхность снаружи, величина гидростатического давления во всех точках поверхности AB имеет те же значения, что и в первом случае, т.к. определяется такой же глубиной. Силы, F г и F в, определяются по тем же формулам, но имеют противоположное направление. При этом под величиной G надо понимать тот же объём жидкости ABCD, несмотря на то, что на самом деле он, в данном случае и не заполнен жидкостью.
11. Запишите уравнение расхода для жидкости, движущейся в трубопроводе.
Рассмотрим движение жидкости по трубе постоянного сечения. Количество жидкости, протекающей через поперечное сечение потока в единицу времени, называют расходом жидкости. Например, Как было показано выше, в разных точках поперечного сечения потока скорость жидкости неодинакова. Около оси трубы скорость максимальна, а по мере приближения к стенкам трубы она уменьшается. Поскольку установить распределение скоростей по поперечному сечению потока часто затруднительно, в инженерных расчетах обычно используют не истинные (локальные) скорости, а среднюю скорость. При этом допускают, что все частицы потока двигаются с одинаковой скоростью. Такая условная скорость жидкости
Тогда уравнение расхода при движении жидкости по трубе постоянного сечения имеет следующий вид:
Объемный расход жидкости V, м3/с, прямо пропорционален скорости жидкости w, м/с, и площади поперечного сечения S, м2. При движении жидкости по соединенным между собой трубам разного диаметра объемный расход жидкости остается постоянным:
Откуда следует, что отношение скоростей в различных сечениях потока обратно пропорционально отношению площадей поперечных сечений этого потока.
Рисунок 1.7 – Течение жидкости по трубам разного диаметра.
Уравнение расхода 1.12 широко используется для расчета диаметра трубопроводов, диаметра аппаратов. Рассмотрим расчет внутреннего диаметра трубы 1. Объемный расход связан с массовым через плотность 2. Площадь поперечного сечения трубы связана с ее внутренним диаметром уравнением 3. Подставим приведенные выше уравнения в уравнение расхода и выразим
где скорость течения жидкости в трубах принимается в пределах
|
||||
|
Последнее изменение этой страницы: 2016-08-25; просмотров: 494; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.179.177 (0.007 с.) |


 – внешнее давление,
– внешнее давление, – площадь горизонтальной проекции поверхности AB,
– площадь горизонтальной проекции поверхности AB, – вес выделенного объёма жидкости.
– вес выделенного объёма жидкости.
 - глубина расположения центра тяжести поверхности AB.
- глубина расположения центра тяжести поверхности AB. и
и  определим полную силу F, действующую на цилиндрическую поверхность
определим полную силу F, действующую на цилиндрическую поверхность
 [м3/с] – объемный расход жидкости.
[м3/с] – объемный расход жидкости. определяется отношением объемного расхода жидкости
определяется отношением объемного расхода жидкости  к площади сечения потока
к площади сечения потока 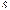 :
: .
. (1.12)
(1.12) .
. . (1.13)
. (1.13) Из уравнения (1.13) можно определить, например, неизвестную скорость
Из уравнения (1.13) можно определить, например, неизвестную скорость  , если известна
, если известна  .
. , если известен расход жидкости
, если известен расход жидкости  , кг/с, текущей по трубе.
, кг/с, текущей по трубе.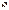 :
:  .
. .
. :
: , отсюда
, отсюда , (1.14)
, (1.14)


