
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные регуляторы непрерывного действия.Содержание книги Поиск на нашем сайте
Выход у линейных регуляторов описывается дифференциальными уравнениями. Промышленностью серийно регуляторы, которые реализуют пять законов регулирования: П – пропорциональные; И – интегральные; ПИ – пропорционально-интегральные; ПД – пропорционально-дифференциальные; ПИД – пропорционально-интегрально-диффиренциальные. В этих регуляторах предусматривается возможность изменения некоторых коэффициентов их дифференциальных уравнений, называемых параметрами настройки регулятора. Такими параметрами настройки являются: - коэффициент передачи (усиления) регулятора; - постоянная времени интегрирования; - постоянная времени дифференцирования; - постоянная времени изодрома; - постоянная времени предварения; Изменяя значения этих параметров, меняют тем самым динамические характеристики регулятора с целью обеспечения качества работы АСР в целом. Значения, при которых достигаются лучшее качество работы системы, называются оптимальными. Кроме органов настройки непосредственно изменяющих коэффициенты дифференциального уравнения регулятора, они, как правило, имеют органы настройки, косвенно влияющие на эти коэффициенты и изменяющие параметры статических характеристик регулятора или режимы его работы. Например, влияющие на чувствительность регулятора, демпфирование входного сигнала, длительность импульсов при релейно-импульсном способе формирования закона регулирования и др. К этим органм настройки относятся: - нечувствительность регулятора; - постоянную времени демпфирования; - длительность импульсов и т.д. Пропорциональные. Передаточная функция W(р) = k (закон регулирования – y = ke) Где e - рассогласование; k – коэффициент усиления (передачи). Настроечный параметр такого регулятора – предел пропорциональности: d = (1 /k) × 100 %, который показывает, какому отклонению регулируемой величины (в % от максимально возможной для данной АСР) соответствует перемещение регулирующего органа из одного крайнего положения в другое. Промышленные П-регуляторы состоят из усилителя, охваченного отрицательной обратной связью с коэффициентом усиления.
(отр. ОС)
В нашем примере усилительное звено имеет передаточную функцию W(p) = k1 и обратная связь коэффициент усиления k2 . Тогда передаточная функция регулятора определится следующим выражением где Wп(p), Wо(p) – передаточные функции прямой и обратной связей соответственно. Подставляя значения передаточных функций в выражение, получим
Достоинство – быстродействие, недостаток - наличие статической ошибки. Интегральные. Передаточная функция W = 1/(Тир) или W = k/р (закон рег-я – y = (1/Ти) ò edt) где Ти – постоянная интегрирования, а 1/Ти часто обозначают как коэффициент передачи k. Параметром настройки регулятора является постоянная времени интегрирования или k. Промышленные И-регуляторы реализуются путем охвата инерционного звена первого порядка с коэффициентом усиления равным единице положительной статической обратной связью. (Статической обратной связью называется такая связь, передаточная функция которой равна 1) Т.е. структурная формула выглядит следующим образом:
 ε ЭС у ε ЭС у
(пол. ОС)
Тогда передаточная функция регулятора определится следующим выражением
где Wп(p), Wо(p) – передаточные функции прямой и обратной связей соответственно. Подставляя значения передаточных функций в выражение, получим
Пропорционально-интегральные. Передаточная функция W = k + 1/(Тир) (закон регулир-я – y = ke + (1/Ти) ò edt) Если при настройке регулятора установить большое значение Ти, то он превратиться в П-регулятор. ПИ-регулятор имеет следующую структурную схему
Т.е. промышленно эти регуляторы состоят из двух параллельно включенных звеньев: усилительного и интегрирующего.
Кроме этой на практике применяется следующая структурная схема ПИ-регулятора.
y = k[e + (1/Тиз) ò edt],
где Тиз - время изодрома. Передаточная функция регулятора W(p) = k[1 + 1/(Тизр)].
Графически законы приведенных регуляторов и будут выглядеть следующим образом: 1 – классический вариант 2 – с общим коэффициентом усиления.
Как видно из графика время изодрома - это время за которое произойдет увеличение пропорциональной составляющей в два раза при действии только интегральной составляющей. Как видно из графиков быстродействие регуляторов с общим коэффициентом выше, причем скорость нарастания интегральной составляющей с увеличением коэффициента усиления будет возрастать. Пропорционально-дифференциальные и пропорционально-интегрально-дифференциальные регуляторы. При наличии дифференциальной составляющей выходной сигнал регулятора изменяется относительного входного сигнала с некоторым опережением равным de/dt и дальнейшем его уменьшении со временем. Когда опережение становится равным 0, выходной сигнал не изменяется, т.е. y = 0. Законы ПД и ПИД в дифференциальной форме имеют следующий вид
ПД –
Передаточные функции этих регуляторов определяются следующими выражениями
Эти промышленные регуляторы образуются путем параллельного соединения динамических звеньев: ПД - пропорционального и дифференциального, ПИД - пропорционального, интегрального и дифференциального. Если у ПИД регулятора устанавливать k = 0, Ти = 0 и Тд = 0 в различном сочетании, то можно получать П, И, ПИ, ПД-законы регулирования. Также, как и для закона ПИ- регулирования, структурные схемы ПД и ПИД-регуляторов могут быть реализованы с общим коэффициентом усиления.
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 721; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.186.153 (0.006 с.) |









 ,
, . Т.к. k1 >> 1, то 1/k2 » 0 1. Тогда
. Т.к. k1 >> 1, то 1/k2 » 0 1. Тогда  .
.


 ,
, .
.
 Данная схема реализует закон вида
Данная схема реализует закон вида Таким образом такой регулятор имеет взаимосвязанные параметры настройки статической и астатической частей по коэффициенту усиления k, т.к. при его настройке изменяться постоянная времени интегрирования. Как видно из приведенных выражений Т = Тиз / k. В первой модели при изменении коэффициента усиления скорость нарастания интегральной составляющей не изменится, во второй она изменится пропорционально.
Таким образом такой регулятор имеет взаимосвязанные параметры настройки статической и астатической частей по коэффициенту усиления k, т.к. при его настройке изменяться постоянная времени интегрирования. Как видно из приведенных выражений Т = Тиз / k. В первой модели при изменении коэффициента усиления скорость нарастания интегральной составляющей не изменится, во второй она изменится пропорционально. , ПИД –
, ПИД –  .
.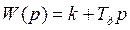 ,
,  ,
,


