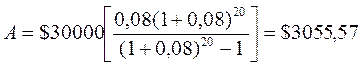Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розрахунок теперішньої вартості грошейСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Досить часто потрібно знати теперішню вартість (Present Value - РV) інвестицій. Ця вартість служить основою для порівняння прибутковості різних проектів та інвестицій за певний період. Отже, теперішня вартість – це грошова вартість майбутніх надходжень чи доходів з поправкою на ставки дисконту. Дисконтна ставка – це відсоткова ставка, яка застосовується до майбутніх платежів, щоб врахувати ризик і непевність, пов'язану з фактором часу. Припустимо, ви хочете визначити теперішню вартість $1000 через 3 роки. Ви сподіваєтесь на щорічний рівень ризику, пов'язаний із реалізацією проекту, в обсязі 10 %. Отже, якщо:
тоді де PV – теперішня вартість коштів; FV – майбутня вартість коштів; R – річна ставка відсотка; N – кількість років. Якщо нарахування відсотків планується більше одного разу за рік, то розрахунок проводять за формулою:
де т – кількість нарахувань за рік, од. Таблиця визначення теперішньої вартості (таблиця 2) економить багато зусиль для підрахування різних її факторів. В ній наведені лише ті значення факторів, які, якщо їх перемножити на майбутню вартість, дають значення теперішньої вартості. В останньому прикладі, де стояло завдання визначити теперішню вартість $1000 через 3 роки, досить було подивитись на кількість років та відповідний відсотковий фактор теперішньої вартості – (PVIF) Ргеsent Value Interest Factor згідно з поданою дисконтною ставкою. Як показано, цей фактор становить 0,751. Щоб одержати теперішню вартість $1000 через 3 роки, маючи дисконт 10%, потрібно перемножити значення фактора на суму теперішньої вартості ($1000 х 0,751=:$751). Отже,
де PVIF – фактор (множник) поточної вартості, стандартні значення якого наведені в таблиці значень фактора поточної вартості (таблиця 2). Таблиця теперішньої вартості економить фінансистам багато часу. Зверніть увагу на те, що за пониження ставки дисконту зростає значення теперішньої вартості. Коли ж ставки зростають, вартість падає. МАЙБУТНЯ ВАРТІСТЬ АНУЇТЕТУ Інвестування грошових коштів у різноманітні програми, створення грошових фондів цільового призначення, пoгaшення банківської заборгованості передбачають виплати, що здійснюватимуться через певні проміжки часу. При цьому виникає ряд послідовнихплатежів, які називаються потоком платежів.
Ануїтет – це ряд послідовних фіксованих платежів, що здійснюються через рівні проміжки часу. Узагальнюючими показниками ануїтету є його майбутня і теперішня вартість. Майбутня вартість ануїтету – це сума всіх членів потоків платежів з нарахованими на них відсотками на кінець періоду, тобто на дату останньої виплати. Вона показує, яку величину представлятиме капітал, що вкладається через рівні проміжки часу впродовж всього терміну ануїтету разом з нарахованими відсотками. Коли платежі здійснюються щороку впродовж N років при відсотковій ставці R, майбутнє значення вартості ануїтету дорівнюватиме:
де FVА – майбутня вартість ануїтету; A 1, A 2,...., An – суми, що сплачуються в кінці кожного періоду в ануїтет; R – відсоткова ставка; N – кількість років.
Якщо платежі за кожен період однакові A 1 = A 2 =... = An = A, то формула набуде вигляду:
де A – ануїтетні платежі; FVIFA – ануїтетний фактор, або відсотковий фактор майбутньої вартостіануїтету, значення якого можна отримати з таблиці 3. Приклад: Інвестор планує вкладати $3000 в ануїтет у кінці кожного року впродовж 10 років. Якщо відсотки в розмірі 9% нараховуються щорічно, то яку суму через 10 років може одержати інвестор? Розв’язання: Використовуємо формулу (1.10):
Таблиці майбутньої вартості ануїтету полегшують підрахунки, в них вже підсумовані проміжні відсоткові фактори майбутньої вартості ануїтету і дається один фактор. Коли платежі відбуваються на початку кожного періоду, то в цьому разі ми маємо справу з авансовим ануїтетом. Його майбутня вартість визначається за формулою: FА = FVA (1 + R), (1.11) де FА – майбутня вартість авансованого ануїтету. Приклад: Інвестор планує вкладати $2000 в ануїтет на початку кожного року впродовж 10 років. Визначте суму, яку отримає інвестор через 10 років за умови, що відсотки нараховуються щорічно в розмірі 6%. Розв’язання: Використовуємо формулу (1.11) для обчислення майбутньої вартості авансового ануїтету:
У цілому ряді практичних задач використовується значення не відсоткового фактора майбутньої вартості ануїтету, а його зворотна величина, яку називають відсотковим фактором фонду відшкодування.
Припустимо, що величина F – це майбутня вартість боргових зобов’язань і для її погашення необхідно створити фонд відшкодування. Для його створення потрібно в кінці кожного періоду вносити певну суму коштів, рівну величині A. Таким чином, величина щорічного внеску до фонду відшкодування дорівнюватиме:
Приклад: Корпорації через 15 років необхідно покрити витрати за випуск облігацій у сумі $10 млн. Вона створює для цього фонд відшкодування і сподівається отримувати 8% щорічно від використання коштів фонду. Яку суму щорічно корпорація повинна вкладати до фонду, щоб акумулювати повністю $10 млн., якщо щорічні платежі вносяться до фонду в кінці кожного року? Розв’язання: Якщо щорічні платежі А до фонду вносяться в кінці кожного року, використовуємо формулу (1.12) для визначення майбутньої вартості звичайного ануїтету:
Отже, корпорація повинна щорічно вкладати до фонду $368295,45 упродовж 15 років, щоб одержати $10 млн.
ТЕПЕРІШНЯ ВАРТІСТЬ АНУЇТЕТУ
При використанні процедур дисконтування грошових потоків при оцінці інвестицій необхідно знати теперішню вартість грошової суми, що може бути отримана в майбутньому. Формула для визначення теперішньої вартості ануїтету матиме вигляд:
де: РVА – теперішня вартість ануїтету; А – сума ануїтету, R – ставка дисконту; N – кількість років або періодів; PVIFA – відсотковий фактор теперішньої вартості ануїтету (таблиця 4). Приклад: Корпорація розраховує отримувати грошові надходження від впровадження нового проекту $5000 щорічно упродовж 10 років. Знайдіть теперішню вартість грошей, яку отримає корпорація, якщо ставка дисконту дорівнює 10%. Розв’язання: Використовуємо формулу (1.13) для визначення теперішньої вартості ануїтету: PVA = $5000 x 6,14446 = $30723.
З формули 1.13 можна вивести формулу для задач по відновленню капіталу.
Приклад: Позичальнику потрібні $30000 для подальшого інвестування. Банк надає позичку на 20 років під 8% річних з рівними щорічними платежами в кінці року. Знайдіть суму, яку повинен сплачувати позичальник у кінці кожного року. Розв’язання: Використовуємо формулу (1.14) для визначення суми, яку повинен сплачувати позичальник у кінці кожного року:
Отже, позичальник повинен сплачувати щорічно $3055,57 упродовж 20 років, щоб повернути банку $30000 і відсотки. ПИТАННЯ ДЛЯ САМОКОНТРОЛЮ 1. Через що змінюється вартість грошей у часі? 2. Яким чином змінюється вартість грошей у часі через інфляцію? 3. Яким чином змінюється вартість грошей у часі через ризик? 4. Яким чином змінюється вартість грошей у часі через схильність до ліквідності? 5. Що являє собою майбутня вартість грошей? 6. Що ви розумієте під теперішньою вартістю грошей? 7. Що ви розумієте під процесом нарощування? 8. Що ви розумієте під процесом дисконтування? 9. Що таке дисконтна ставка? 10. Як розрахувати майбутню вартість грошей? 11. Що потрібно знати для підрахунку теперішньої вартості грошових надходжень? 12. Що таке ануїтет? 13. Наведіть два приклади звичайних ануїтетів. 14. Що Ви розумієте під майбутньої вартістю ануїтету? 15. Що таке теперішня вартість ануїтету? 16. Сформулюйте основний принцип вартості грошей в часі. 17. У чому економічний зміст концепції вартості грошей в часі? 18. Перерахуйте чотири основні елементи, що пов'язані між собою в концепції вартості грошей в часі.
19. У чому економічний зміст норми прибутковості інвестування грошей? 20. Запишіть основну формулу теорії складних відсотків. 21. Як змінюється майбутня вартість грошей при збільшенні тривалості інвестування? 22. Сформулюйте приклад практичного використання сучасного значення грошей. 23. Яка вартість грошей є реальною: теперішня чи майбутня? 24. Коли процес інвестування стає невигідним? 25. Коли процес інвестування стає збитковим? 26. Як проводиться процес нарощування і дисконтування грошових потоків? 27. Який грошовий потік називається ануїтетом? 28. Як визначити теперішню і майбутню вартість ануїтету? 29. Як влаштовані і навіщо використовуються фінансові таблиці? 30. Якщо порівняльна ефективність вкладення в реальні активи і фінансові інструменти однакова, то як вона зміниться при збільшенні норми прибутковості?
ПРАКТИЧНІ ЗАВДАННЯ
Задача 1 Позичка в розмірі 80 000 грн. видана на півроку за простою ставкою відсотків під 23 % річних. Визначити нарощену суму.
Задача 2 Позика в розмірі 15 000 грн. видана з 1 березня до 5 грудня під 28 % річних. Визначити розмір нарощеної суми для різних варіантів (звичайного й точного) розрахунку відсотків. Задача 3 Позика в розмірі 27 000 грн. видається на 4 роки. Ставка відсотків за перший рік – 35%, а за кожне наступне півріччя вона зменшується на 2%. Визначити нарощену суму у кінці 4-х річного періоду.
Задача 4 Визначити період нарахування, за який початковий капітал у розмірі 18 000 грн. зросте до 43 000 грн., якщо використовується проста ставка відсотків – 31% річних? Задача 5 Визначити просту ставку позичкових відсотків, при якій початковий капітал у розмірі 13 000 грн. досягне 18 000 грн. через рік.
Задача 6 Позика видається під просту ставку позичкових відсотків 30% річних на 235 днів. Розрахувати суму, що одержав позичальник і суму відсоткових грошей, якщо треба повернути 75 000 грн.
Задача 7 Позика в розмірі 3600 грн. видана на 500 днів під просту ставку позичкових – 36% річних. Визначити суму відсоткових грошей і суму, що повинна бути повернута. Задача 8 Фірмі надана короткострокова позика (на умовах простих відсотків) у розмірі 12 тис. грн. Визначити нарощену суму на підставі таких даних: а) терміном на 5 місяців під 60% річних; б) терміном на 3 місяці під 55% річних; в) терміном на 6 місяців під 40% річних.
Задача 9 Необхідно знайти суму простого відсотка за рік при наступних умовах: початкова сума вкладу – 1000 грн., відсоткова ставка, що виплачується щоквартально, – 20%.
Задача 10 Визначити, скільки отримає інвестор за 5 років, якщо вкладе 150 тис. грн. під 15% річних. Відсотки нараховуються раз на рік за умовами складного нарахування. Порівняти результати з простим нарахуванням відсотків.
Задача 11 Яка майбутня вартість 1000 грн., вкладених під 12% річних на 5 років з нарахуванням відсотків раз на півроку та тричі на рік.
Задача 12 Підприємство має на рахунку у банку 1,2 млн. грн. Банк нараховує 25% річних. Існує пропозиція ввійти всім капіталом до спільного підприємства. При цьому прогнозується подвоєння капіталу через 5 років. Чи варто приймати таку пропозицію? Задача 13 У вашому розпорядженні є 10 млн. грн. Ви хотіли б потроїти цю суму через 7 років. Яким є мінімально прийнятне значення відсоткової ставки?
Задача 14 Фірмі необхідно нагромадити 2 млн. грн. для придбання через 10 років будівлі під офіс. Найбезпечнішим способом нагромадження є придбання серій безризикових державних цінних паперів, що генерують річний дохід за ставкою 8 % річних з нарахуванням відсотків кожні півроку. Яким має бути початковий внесок фірми? Задача 15 Розрахуйте теперішню вартість 1000 грн., які будуть отримані через 12 років, зважаючи на те, що ставка дисконтування становить 12 %.
Задача 16 Розрахуйте теперішню вартість 623 грн., що будуть отримані через 8 років, плюс 1092 грн., які будуть отримані через 8 років після цього, за умови, що відсоткова ставка становить 7 %. Задача 17 Розрахувати суму грошових коштів, яку необхідно вкласти до банку „сьогодні”, якщо депозитна ставка складає 20% річних для того, щоб: а) через 4 роки на банківському рахунку було 20 тис. грн.; б) через 3 роки на банківському рахунку було 25 тис. грн.; в) через 5 років на банківському рахунку було 30 тис. грн.
Задача 18 Дати оцінку рішенню інвестора. Інвестор має вільні грошові кошти в сумі: а) 1223 тис. грн.; б) 683 тис. грн.; в) 500 тис. грн. Чи зможе він придбати обладнання А вартістю 1200 тис. грн. через 2 роки та обладнання Б вартістю 700 тис. грн. через 4 роки, якщо „сьогодні” інвестує кошти до банку під 10% річних? Задача 19 Розрахуйте відсоткову ставку банку, якщо у кінці 5-річного періоду підприємство отримало 120 тис. грн., поклавши 80 тис. грн. на депозит.
Задача 20 Визначити майбутню вартість інвестицій, якщо: а) термін вкладу складає 3 роки, ставка відсотку за депозитом - 18% річних; б) термін вкладу складає 5 років, ставка відсотку за депозитом – 20% річних; в) термін вкладу складає 6 років, ставка відсотку за депозитом – 30% річних. Фірма вкладає до банку на депозит грошову суму у розмірі 850 тис. грн.
Задача 21 Компанія аналізує доцільність вкладення в її розвиток $15000 власних коштів на умовах, що через 2 роки вони повинні принести $20000. При цьому компанія хоче мати річний приріст не менше 10%. Чи реальні такі умови?
Задача 22 $2000 інвестуються під 12% річних на 10 років. Визначити нарощену суму.
Задача 23 Визначити, яку суму слід покласти на депозит, щоб через 3 роки власник депозиту одержав 3000 гривень. Застосовані ставки: а) 8 % річних; б) 12% річних. Задача 24 Визначити майбутню вартість $500, вкладених на 8 років під 12% річних.
Задача 25 Яка майбутня вартість ануїтету $250 через 5 років, відраховуючи 10% річних? Задача 26 П’ять платежів по $1000 кожен потрібно вносити у кінці кожного року, враховуючи, що річна ставка відсотків за період між платежами становить 12%. Скільки коштів буде отримано у кінці останнього періоду? Як зміниться фінансовий результат, якщо кошти будуть вноситись на початку кожного року?
Задача 27 Визначити, що вигідніше: обрати $5000 зараз чи $850 щороку протягом 5 років, якщо річна ставка становить 8%.
Задача 28 Розрахуйте теперішню вартість 10-ти річного ануїтету вартістю 100 грн. за ставкою 20 % річних. Задача 29 Розрахуйте теперішню вартість 250 грн., які отримуватимуться щорічно протягом 10 років, плюс 1200 грн., які отримуватимуться протягом 15 років, за умови, що річна відсоткова ставка становитиме 11 %.
Задача 30 Державні облігації можна погасити за $25000 через 10 років, коли прийде термін їх погашення. Яка тепер вартість облігації, якщо дисконтна ставка на біржі 9%? Задача 31 Визначити теперішню вартість 200000 грн., які буде виплачено через 4 роки. На первісну суму на протязі цього періоду нараховуються складні відсотки за ставкою 8% річних? Задача 32 Інвестор має 2-х дітей віком 17 та 18 років. Він хоче подарувати їм до 20 річчя по $10000. Яку первісну суму він повинен вкласти під 8% річних?
Задача 33 Інвестор через 3 роки хоче одержати $13310. Яку первісну вартість він повинен вкласти сьогодні під 10% річних?
Задача 34 Ви взяли банківську позику в $6000 на 4 роки. Річна ставка 12%. Чи можете ви визначити, яку суму позики треба щорічно гасити? Задача 35 Визначити теперішню вартість 20 000 грн., що буде виплачена через 5 років при використанні ставки складних відсотків 18 % річних?
Задача 36 Початкова сума боргу дорівнює 15 000 грн. Визначити нарощену суму через 4 роки, використовуючи нарахування складних відсотків за ставкою 30% річних. Задача 37 Підприємство планує інвестувати вільні кошти в розмірі 150 тис. грн. на 4 роки. Визначте найбільш ефективний варіант розміщення коштів на депозитний рахунок банку з декількох альтернативних. За першим варіантом планується щорічне нарахування складних відсотків за ставкою 18%, за другим варіантом – щомісячне нарахування складних відсотків за ставкою 14%, за третім варіантом – щорічне нарахування простих відсотків за ставкою 24%.
Задача 38 Підприємство вирішило вкласти вільні кошти в розмірі 20 тис. грн. строком на 3 роки. Є три альтернативних варіанти вкладень. За першим варіантом кошти вносяться на депозитний рахунок банку із щорічним нарахуванням складних відсотків за ставкою 21%, за другим варіантом — щорічне нарахування 25%, за третім варіантом – щомісячне нарахування складних відсотків за ставкою 18% річних. Необхідно, не враховуючи рівень ризику, визначити найкращий варіант вкладення коштів.
Задача 39 Підприємство планує через три роки придбати нове обладнання. Очікується, що майбутня вартість устаткування становитиме 900 тис. грн. Визначте, яку суму коштів потрібно помістити на депозитний рахунок банку, щоб через три роки одержати достатню суму коштів, якщо ставка за депозитними рахунками встановлена в розмірі 17% із щомісячним нарахуванням відсотків або 21% з нарахуванням складних відсотків один раз на рік. Задача 40 Підприємство планує через чотири роки придбати приміщення під склад. Відповідно до експертних оцінок, майбутня його вартість становитиме 560 тис. грн. Визначте, яку суму коштів необхідно розмістити на депозитний рахунок банку, щоб через чотири роки одержати достатню суму коштів, якщо ставка за депозитними рахунками установлена в розмірі 15% із щомісячним нарахуванням відсотків, 17% – із щоквартальним нарахуванням відсотків або 25% з нарахуванням складних відсотків один раз на рік. Зробіть висновки.
Задача 41 Необхідно визначити суму дисконту за простим відсотком за рік при таких умовах: кінцева сума вкладу в розмірі 1000 грн., дисконтна ставка – 20% в квартал. Дисконт розраховується як різниця між FV і PV.
Задача 42 Необхідно визначити реальну майбутню вартість інвестованих грошових коштів при наступних умовах: об’єм інвестиції – 200 млн. грн., період інвестування – 2 роки, використана відсоткова ставка з урахуванням інфляції – 20% в рік. Задача 43 Застосуйте основну формулу визначення майбутньої вартості і підрахуйте, скільки отримає інвестор за 6 років, якщо він вклав $800000 під 12% річних?
Задача 44 Визначити майбутню вартість через 2 роки депозиту на $100, якщо річний відсоток становить 12%. Відсотки нараховуються щомісяця.
Задача 45 Застосуйте основну формулу визначення майбутньої вартості і підрахуйте, скільки отримає інвеститор за 5 років, якщо він вклав $100 під 8% річних. Відсотки нараховуються раз на рік. Задача 46 За допомогою таблиці визначте майбутню вартість $500, вкладених на 8 років під 12% річних. Задача 47 Яка майбутня вартість ануїтету $250 через 5 років, враховуючи 10% річних? Задача 48 Майбутня вартість ануїтету через 4 роки – $4000. Якщо відсоткова ставка дорівнює 8%, який буде ануїтет?
Задача 49 Державні облігації можна погасити за $25000 через 10 років, коли прийде термін їх погашення. Яка теперішня вартість облігації, якщо дисконтна ставка на біржі 9%? Задача 50 Що Ви вибираєте: $4500 готівкою чи $1200 щороку протягом чотирьох років? Річна відсоткова ставка дорівнює 10%.
Задача 51 Визначте майбутню вартість $1200 через 4 роки, якщо: а) складний відсоток нараховується щорічно в розмірі 12%; б) складний відсоток нараховується раз на півріччя в розмірі 12%; в) складний відсоток нараховується щоквартально в розмірі 16%; г) складний відсоток нараховується щомісячно в розмірі 24%.
Задача 52 Інвестор купував у 2000 році пакет акцій за ціною $20 за акцію. Якщо він у 2010 році продасть цей пакет за $45 за акцію, то який буде щорічний темп зростання ціни акції? Задача 53 Власник ферми продав землю за ціною $3235 за 1 га. Він каже, що володів землею 20 років і що вартість землі зростала щорічно на 11%. За яку ціну фермер купував землю? Задача 54 Через скільки років ви зможете подвоїти ваші гроші у розмірі $1000, якщо їх вартість щорічно зростає на 10 %? Задача 55 Припустимо, що середня вартість будинку в 2008 році була $70000. Який щорічний рівень інфляції має бути, щоб середня вартість будинку була $100000 у 2012 році? Задача 56 Ви бажаєте розмістити депозит в одному з трьох банків. Кожен банк сплачує 12% річних. Банк А нараховує відсотки щорічно, банк В — щопівріччя, банк С — щоквартально. До якого банку необхідно вкласти кошти, якщо ви плануєте отримати депозит через 5 років? Задача 57 Інвестор має $10000. Він може вкласти цю суму на 15 років під 10% річних. Яку суму грошей він одержить через 15 років?
Задача 58 Визначити теперішній розмір суми 20 000 грн., що буде виплачена через 5 років при використанні ставки складних відсотків 18 % річних?
Задача 59 Інвестор планує вкладати $8000 в ануїтет на початку кожного року впродовж 8 років. Якщо відсотки нараховуються щорічно в розмірі 8%, визначте суму, яку отримає інвестор через 8 років.
Задача 60 Інвестор планує вкладати $15000 в ануїтет у кінці кожного року впродовж 6 років. Якщо відсотки нараховуються щорічно в розмірі 8%, визначте суму, яку отримає інвестор через 6 років.
Задача 61 Інвестор має $10000. Він може вкласти гроші в ощадний сертифікат під 8% річних на 5 років. Інвестор очікує, що відсоткова ставка сертифіката зростатиме на 3% кожні 5 років. Яку суму коштів інвестор отримає через 15 років?
Задача 62 Ви бажаєте купити будинок за $75000. Один банк згоден дати вам кредит під 9% річних терміном на 20 років з щорічними виплатами плюс виплата $15000 у момент отримання кредиту. Інший банк надає кредит під 10% річних, але терміном на 25 років і теж з виплатою $15000 у момент отримання кредиту. Який з варіантів вигідніший? Задача 63 Працівнику зараз 40 років, пенсійний вік — 65 років. Він може інвестувати $3500 щорічно до пенсійного фонду в кінці кожного року під 14% річних. Працівник сподівається прожити 80 років. Після виходу на пенсію він планує отримувати прибуток від інвестованих до фонду коштів у розмірі 8% річних. Визначте суму, яку нагромадить працівник у віці 65 років і розмір щорічної пенсії. Задача 64 Початкова вкладена сума дорівнює 15 000 грн. Визначити нарощену суму через три роки при використанні простої і складної ставок відсотків у розмірі 32 % річних. Вирішити цей приклад також для випадків, коли відсотки нараховуються раз у півроку та поквартально.
Задача 65 Інвестору через 6 років необхідно віддати банку кредит у сумі $10000. Він створює для цього фонд відшкодування і сподівається отримувати 5% щорічно від використання коштів фонду. Яку суму щорічно інвестор повинен вкладати до фонду, щоб отримати $10000, якщо щорічні платежі вносяться до фонду в кінці кожного року?
Задача 66 Сьогодні на рахунку підприємства у комерційному банку є 100 тис. грн., на які банк нараховує 12% річних раз на рік за умовами складного нарахування. Яку суму підприємство може знімати щорічно з рахунку, щоб їх вистачило рівно на 10 років, при умові, що банк продовжуватиме нараховувати відсотки на залишок суми на рахунку?
Задача 67 Здійснивши вдосконалення технологічного процесу, підприємство протягом наступних років планує щорічне збільшення грошового доходу на 3000 грн. Ці гроші воно збирається негайно вкладати під 8% річних, бажаючи через 5 років отримати суму для придбання нового обладнання. Яку суму грошей підприємство отримає через 5 років?
Задача 68 Проаналізуйте два варіанти накопичення засобів за схемою ануїтету (надходження грошових засобів здійснюється в кінці відповідного часового інтервалу). Варіант 1: на депозит кожні півроку вноситься вклад 500 грн. на умовах піврічного нарахування 8% річних. Варіант 2: здійснюється щорічний вклад в розмірі 1000 грн. на умовах 9% річних при щорічному нарахуванні відсотків. Визначте: а) яка сума буде на рахунку через 10 років при реалізації кожного варіанту? Який варіант вигідніший? б) чи зміниться Ваш вибір, якщо відсоткова ставка у варіанті 2 буде знижена до 8%? Задача 69 Підприємству необхідно погасити кредит 30000 грн., взятий на 5 років під 15% річних. Умовами договору встановлена схема погашення кредиту, яка полягає у здійсненні рівномірних платежів, які необхідно сплачувати після першого року користування кредитом протягом всього терміну, передбаченого договором. Визначте суму платежів, які необхідно сплачувати щороку.
Задача 70 Підприємство має дві альтернативні можливості придбання обладнання. За першим варіантом умовами договору передбачено, що підприємство повинно щоквартально сплачувати банку (лізингодавцю) 2500 грн. протягом 10 років. За другим варіантом підприємство може придбати аналогічне обладнання, за яке відразу необхідно сплатити 10000 грн. Дисконтна ставка – 10%. Запропонуйте керівництву підприємства оптимальний варіант інвестування.
Таблиця 1
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 4945; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.136.229 (0.015 с.) |

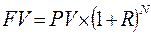 ,
,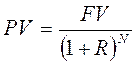 , (1.6)
, (1.6)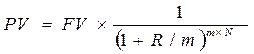 , (1.7)
, (1.7)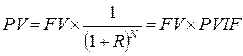 , (1.8)
, (1.8)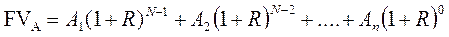 , (1.9)
, (1.9)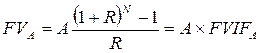 , (1.10)
, (1.10)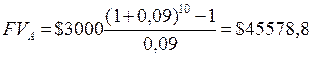 .
.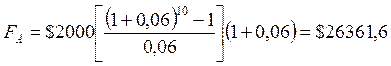 .
.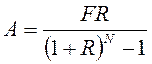 (1.12)
(1.12)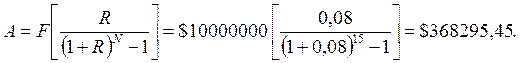
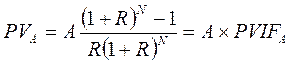 , (1.13)
, (1.13)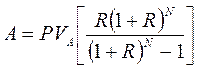 (1.14)
(1.14)