Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розділ 1: «Використання математичних моделей для обґрунтування управлінських рішень в ситуації ризику»Содержание книги
Поиск на нашем сайте Зміст Вступ. 4 Розділ 1: «Використання математичних моделей для обґрунтування управлінських рішень в ситуації ризику». 5 1.1 Поняття моделі 5 1.2 Прийняття рішень в умовах ризику. 7 1.3 Приклади математичних моделей в ситуації ризику. 7 1.3.1 Задача оптимального управління портфелем фінансових активів. 7 1.3.2. Задача оптимізації валютного резерву. 11 1.3.3. Оптимізація кредитного портфеля. 13 Розділ 2: «Розв'язок економічних задач». 17 2.1 Оптимальне перевезення вантажів. 17 Постановка задачі 17 Економіко-математична модель задачі 17 Методика реалізації моделі 18 Висновок. 20 2.2 Оптимізація порожнього пробігу автотранспорту. 20 Постановка задачі 20 Економіко-математична модель задачі 21 Методика реалізації моделі 22 Висновок. 24 2.3 Взаємозалік боргів підприємства. 24 Постановка задачі 24 Економіко-математична модель задачі 25 Методика реалізації моделі 25 Висновок. 28 2.3 Визначення оптимальної послідовності виготовлення деталей. 28 Постановка задачі 28 Економіко-математична модель задачі 29 Методика реалізації моделі 30 Висновок. 34 Висновок. 35 Література: 36
Вступ На сучасному етапі розвитку науки і техніки в усіх галузях людської діяльності знаходять широке застосування методи моделювання економіки. Тому важливого значення набуває використання економічно-математичних методів і моделей у практичній діяльності. Важливою є умова та особливості їх застосування залежно від мети дослідження, прийнятої системи гіпотез. Основним інструментальним та ефективним методом дослідження систем є метод моделювання, тобто спосіб теоретичних і практичних дій, спрямованих на створення та використання моделей. Під моделлю можна розуміти образ реального об’єкта (процесу) в матеріальній чи ідеальній формі (тобто такий, який описано знаковими засобами певною мовою), що відображає суттєві властивості модельованого об’єкта (процесу) й заміщує його в ході дослідження й управління. Метод моделювання ґрунтується на принципі аналогії, тобто можливостях вивчення реального об’єкта не безпосередньо, а шляхом дослідження подібного йому й більш доступного цьому дослідженню об’єкта – його моделі. Мета курсової – навчитися застосовувати методологію, методику та інструментарій економіко-математичного моделювання в теоретичних дослідженнях та використовувати здобуті знання у практичній діяльності. Для досягнення мети поставлені наступні задачі: 1) Визначити оптимальний план перевезення вантажів; 2) Оптимізувати порожній пробіг автотранспорту; 3) Перерозподілити борги підприємства; 4) Визначити оптимальну послідовність обробки деталей на верстатах за критеріями: a. критерій найшвидшого закінчення робіт; b. критерій мінімізації перебування деталей в процесі виробництва; c. критерій мінімізації простоїв верстав. Розділ 1: «Використання математичних моделей для обґрунтування управлінських рішень в ситуації ризику» Поняття моделі Термін «модель» походить від латинського слова «modulus» — зразок, норма, міра. Модель — це об’єкт, що заміщує оригінал і відбиває найважливіші риси і властивості оригіналу для даного дослідження, даної мети дослідження за обраної системи гіпотез. Математична модель — це абстракція реальної дійсності (світу), в якій відношення між реальними елементами, а саме ті, що цікавлять дослідника, замінені відношеннями між математичними категоріями. Ці відношення зазвичай подаються у формі рівнянь і/чи нерівностей, відношеннями формальної логіки між показниками (змінними), які характеризують функціонування реальної системи, що моделюється. Сутність цієї методології полягає в заміні вихідного об’єкта його «образом» — математичною моделлю — і подальшим вивченням (дослідженням) моделі на підставі аналітичних методів та обчислювально-логічних алгоритмів, які реалізуються за допомогою комп’ютерних програм. Робота не із самим об’єктом (явищем, процесом), а з його моделлю дає можливість відносно швидко і безболісно досліджувати його основні (суттєві) властивості та поводження за будь-яких імовірних ситуацій (це переваги теорії). Водночас обчислювальні (комп’ютерні, симулятивні, імітаційні) експерименти з моделями об’єктів дозволяють, спираючись на потужність сучасних математичних та обчислювальних методів і технічного інструментарію інформатики, ретельно та досить глибоко вивчати об’єкт у достатньо детальному вигляді, що недоступно суто теоретичним підходам (це перевага експерименту). Не дивно, що методологія математичного моделювання бурхливо розвивається, охоплюючи аналіз надзвичайно складних економічних і соціальних процесів. Технічні, технологічні, економічні, політичні та інші системи, що їх вивчає сучасна наука, все меншою мірою піддаються дослідженню (в необхідній комплексності та точності) звичайними теоретичними методами, хоча останні є надзвичайно важливими. Безпосередній натурний експеримент над ними є надто тривалим, дорогим, часто навіть небезпечним чи просто неможливим, особливо це стосується економічних систем і процесів. Тому математичне моделювання є неминучою складовою науково-технічного прогресу.
Рис. 1.1. Узагальнена схема математичного моделювання Створивши тріаду: «модель—алгоритм—програма», дослідник (системний аналітик) отримує універсальний, гнучкий і відносно дешевий інструмент, який тестується в «пробних» обчислювальних експериментах. Після того як адекватність (достатній рівень відповідності, зважаючи на цілі та взяту систему гіпотез) тріади щодо вихідного об’єкта засвідчена, з моделлю проводять різноманітні та детальні «досліди», які дають нову інформацію про необхідні якісні та кількісні властивості й характеристики об’єкта. Процес моделювання супроводжується поліпшенням та уточненням, за необхідності, всіх складових (ланок) тріади. Якщо ж аналізувати проблеми моделювання економічних систем, де необхідно брати до уваги «людський чинник», тобто коли йдеться про аналіз слабоформалізованих об’єктів, то до цих вимог необхідно додати ще низку, зокрема, акуратне розмежування математичних і побутових термінів, завбачливе застосування вже готового математичного апарату до вивчення явищ і процесів (пріоритетним є шлях «від задачі до методу», а не навпаки) та інші. Ситуація ризику У цій моделі величини dj вважаються невідомими, але є статистичні дані про них за певний відрізок часу, по яких ми можемо визначити їх математичні сподівання та дисперсії, використавши статистичні дані за попередні періоди, і зробити певні висновки. Математичне сподівання величини dj визначається як середнє значення цієї величини за кілька періодів. Позначається воно Дисперсія величини dj визначає, наскільки далеко розміщені значення цієї величини від її математичного сподівання. Дисперсія позначається
Іще одним важливим параметром є коефіцієнт кореляції, який позначається
Коли ми приймаємо рішення за умов ризику нам потрібно визначитись із нашим ставленням до нього. Є три види ставлення: нейтральне (працюємо так, ніби знаємо dj і не звертаємо уваги на втрати), позитивне і негативне (не допускаємо жодного ризику). Розглянемо спочатку модель задачі для нейтрального ставлення до ризику. У цій моделі ми намагаємось зробити найбільшим середній дохід, не звертаючи уваги на можливі відхилення від середніх.
Розглянемо тепер варіант, коли інвестор ставиться до ризику позитивно. Тоді він повинен вибрати такий варіант, який дає найбільше середнє значення і найбільш можливе відхилення цього значення.
Обмеження в задачі залишаються тими ж. Розглянемо випадок негативного ставлення до ризику.
Дана задача є двокритеріальною. Критеріями вважаються середнє значення та дисперсія. В принципі, можливо, що ці критерії суперечать один одному, тобто оптимальне значення одного з них дає значення далеке від оптимального значення іншого. Розв’язання двокритеріальної задачі здійснюється в кілька етапів: 1. Для обох критеріїв визначаються найменше та найбільше можливі значення (zmin, zmax; σ2min, σ2max). 2. Якщо для одного із критеріїв мінімальне значення дорівнює максимальному, то цей критерій взагалі відкидається. Якщо ж ці значення не рівні, то складається загальний критерій:
Знак „+” відповідає позитивному ставленню до ризику, а знак „” негативному. Далі потрібно розв’язати задачу визначенням найбільшого значення критерію u. 3. Якщо інвестор не погоджується з нашим рішенням, то він повинен вказати межі для середнього значення і дисперсії, які його влаштовують. 4. Потім ми повинні визначити реальність варіантів, які визначив інвестор і здійснюємо корекцію варіантів. Якщо вони не реальні, то послаблюємо вимоги, щоб зробити їх реальними. Якщо ж вимоги реальні, то корекція може посилити їх. 5. Визначається найбільш ефективний фінансовий портфель, розв’язок передається інвесторові. 6. Якщо інвестор погодився з розв’язком, то задача розв’язана, інакше повертаємось на етап №4. Ситуація ризику У цій ситуації значення цінностей wj1 невідомі, але є статистичні дані за кілька періодів на основі яких для кожного виду валюти ми можемо визначити математичне сподівання та дисперсію відносної цінності цієї валюти.
σj2 – дисперсія. Дана задача є двокритеріальною. Першим критерієм є математичне сподівання загальної цінності. Його бажано зробити найбільшим. Другим критерієм є дисперсія загальної цінності. Її бажано зробити найменшою.
Для розв’язання цієї задачі ми складаємо загальний критерій із двох даних критеріїв.
Розв’язавши дану задачу, ми одержуємо оптимальний план для якого визначене середнє значення і дисперсія. Одержане рішення передається на затвердження особі, що приймає рішення, яка може або погодитися з цим планом або визначити інші межі для середньої цінності дисперсії. Позначимо через Для перевірки даних на реальність ми вводимо додаткову змінну t. Ця змінна характеризує якість плану по відношенню до вимог особи, що приймає рішення. Найбільшим значенням цієї змінної є 1. t=1 означає, що ми можемо не тільки виконати вимоги замовника, а й досягти максимального середнього значення й мінімальної дисперсії. Значення t>0 означає, що вимоги замовника реальні і їх можна покращити. t=0 означає, що вимоги реальні, але покращити їх не можна. t<0 означає нереальність вимог замовника. Особливістю змінної t є той факт, що вона включається як до критерію так і до обмеження. Значення цієї змінної визначається як розв’язок такої задачі:
Обмеження:
y є Y означає, що план є допустимим, тобто задовольняє обмеженням початкової задачі. Розв’язавши цю задачу знаходимо значення t по якому потім розв’язуємо другу задачу:
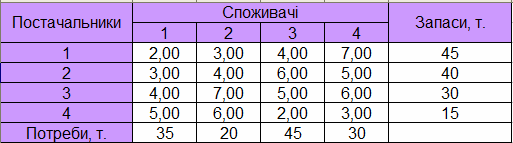
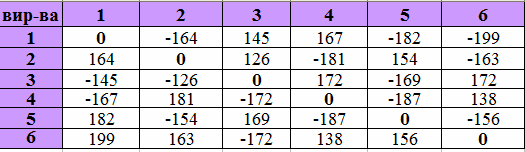
Постановка задачі Із 4 складів в 4 крамниці потрібно перевезти борошно. Відомі запаси борошна на кожному складі, потреби крамниць і вартість перевезення 1т борошна з кожного складу в кожну крамницю. Визначити такий план перевезень, щоб сумарна вартість перевезення була мінімальною, борошно все вивезене, а потреби крамниць задоволені. Розглядається закрита модель, за якою запаси постачальників дорівнюють потребам споживачів. Початкові дані наведені в таблиці 2.1. Таблиця 2.1 – Початкові дані
Методика реалізації моделі Після створення таблиці початкових даних, у другу таблицю запишемо кількості перевезених вантажів від кожного постачальника до кожного споживача. На початку ці величини приймаємо рівними 0. Нижній рядок і крайній правий стовпець цієї таблиці відводимо для запису загальної кількості вантажів, які перевезені від кожного постачальника до кожного споживача (суми по рядках і стовбцях). Третя таблиця визначає вартість перевезень. В її клітинки запишемо добутки кількості вантажу з другої таблиці на вартість перевезення одиниці вантажу з першої. Нижній рядок відводимо для загальної вартості перевезень до кожного споживача, сума по стовбцям (Рис. 2.1). Загальна вартість усіх перевезень визначається як сума значень цього рядка. Клітинка загальної вартості вибирається як цільова в "Поиске решения". Змінними клітинками є кількість вантажу, який перевозиться від і-того постачальника до j-того споживача. Обмеження: 1) загальна кількість перевезень до кожного споживача дорівнюють його потребам; 2) загальна кількість перевезень від кожного постачальника дорівнюють його запасам; 3) всі перевезення невід’ємні та є цілими числами; 4) всі перевезення не перевищують загальних запасів.
Рис. 2.1 – Формули для моделі оптимального перевезення вантажів Вікно "Поиска решения" зображено на рисунку 2.2.
Рис. 2.2 – Вікно "Поиска решения" для моделі оптимального перевезення вантажів Після проведення обчислень було отримано наступні результати (Рис. 2.3).
Рис. 2.3 – Результати задачі оптимального перевезення вантажів Висновок Так як, за умовою задачі модель збалансована, то потреби крамниць були задоволені, а все борошно вивезене. Так 1-ий постачальник задовольнив потреби 1 та 2 крамниць, 2-й постачальник – 1, 2 та 4 крамниць, 3-й та 4-й постачальник задовольнили потреби 3-ї крамниці. У результаті було визначено оптимальний план перевезень, сумарна мінімальна вартість при якому становить 470 ум. од. Постановка задачі Споживачам потрібні вантажі, які зосереджені в різних постачальників, перевезення здійснюється автотранспортом одного типу, після розвантаження у споживача автомобіль повертається за вантажем до постачальника, але не обов'язково до попереднього; для кожного постачальника відомо, яку кількість вантажу до якого споживача потрібно перевезти (кількість вантажу дорівнює кількості рейсів). Скласти план перевезень, щоб загальний порожній пробіг автомобілів був найменшим. Початкові дані зображено на рисунку 2.4.
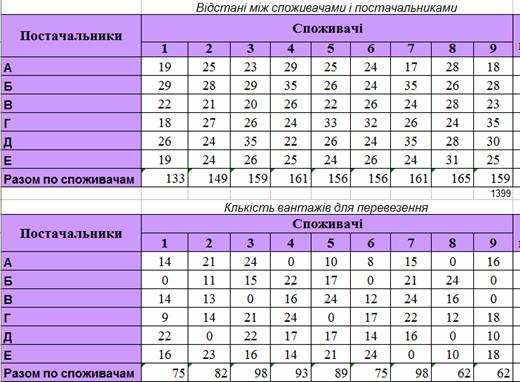
Рис. 2.4 – Початкові дані для задачі оптимізації порожнього пробігу Методика реалізації моделі У першій таблиці запишемо відстані від постачальників до споживачів. У другій таблиці вкажемо кількість рейсів, які потрібно зробити від постачальників до споживачів. У цій же таблиці визначаємо загальну кількість рейсів для постачальників і споживачів. У третій таблиці визначаємо кількість порожніх рейсів від споживачів до постачальників. На початку вони приймають значення 0. Визначаємо загальну кількість цих рейсів за порядками. У четвертій таблиці визначаємо порожній пробіг. Для цього відстані між постачальниками і споживачами множимо на кількість рейсів (тобто, елементи першої таблиці множимо на відповідні елементи третьої). Формули для розрахунків зображені на рисунку 2.5.
Рис. 2.5 – Формули для моделі оптимізації порожнього пробігу автотранспорту Визначаємо загальний порожній пробіг за порядками і стовпчиками та загальний порожній пробіг за всією таблицею. Цей пробіг є цільової клітиною "Поиска решения" і приймає найменше значення. Змінними є клітинки третьої таблиці. Обмеження: 1) елементи третьої таблиці є цілими та невід'ємними; 2) кількість рейсів від постачальника дорівнює кількості порожніх рейсів до постачальника; 3) кількість рейсів до споживача дорівнює кількості порожніх рейсів від споживача.
Вікно "Поиска решения" зображено на рисунку 2.6.
Рис. 2.6 – Вікно «Поиска решения» для моделі оптимізації порожнього пробігу автотранспорту Отримані результати зображено на рисунку 2.7.
Рис. 2.7 – Результати задачі оптимізації порожнього пробігу автотранспорту Висновок Отже, після проведення обчислень можна сказати, що найбільшу кількість порожніх рейсів зробив постачальник Е, а найменше - постачальник А, відповідно 140 та 107. За умовою задачі потрібно було скласти такий план перевезень, щоб загальний порожній пробіг автомобілів був найменшим, у даному випадку він дорівнює 15 922 км. Постановка задачі Деяке підприємство складається з кількох видів виробництв, які заборгували один одному кошти, потрібно перерозподілити борги так, щоб сума всіх взаємних боргів була найменшою, а сальдо кожного виробництва не змінилося. Початкові дані наведені в таблиці 2.2. Таблиця 2.2 – Початкові дані для задачі взаємозаліку боргів підприємства
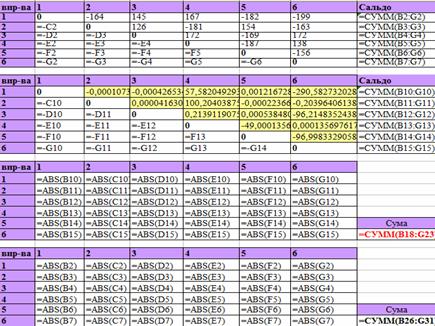
Методика реалізації моделі Взаємні заборгованості підприємств запишемо в таблицю. Кількість рядків таблиці дорівнює кількості стовпчиків та кількості підприємств. На перетині i-го рядка і j-го стовпчика запишемо борг і-го підприємства j-му. Якщо цей борг від'ємний, то і-те підприємство віддає борг j-му; якщо додатний – навпаки. По головній діагоналі таблиці з лівого верхнього кута в правий нижній пишемо 0. Вище діагоналі запишемо довільні початкові дані, а нижче діагоналі запишемо вираз:
Для даної таблиці визначаємо суми за рядками – це сальдо Друга таблиця, такої ж розмірності, як і перша, призначена для одержання оптимального рішення. По головній діагоналі пишемо 0, вище неї – також 0. Нижче записуємо вираз, який забезпечує рівність:
Для даної таблиці теж визначаємо сальдо. Третя таблиця містить абсолютні величини значень другої таблиці (функція ABS()).Визначаємо суму елементів цієї таблиці – це оптимальне значення критерію. Четверта таблиця включає абсолютні елементів першої таблиці. Вона необхідна для порівняння поточного та оптимального станів заборгованості. Формули для розрахунків зображені на рисунку 2.8.
Рис. 2.8 – Формули для моделі взаємозаліку боргів підприємства
Цільовою клітинкою для "Поиска решения" – сума всіх елементів третьої таблиці, вона повинна прийняти мінімальне значення. Змінними клітинками являються клітинки другої таблиці вище головної діагоналі. Обмеження: - індивідуальні сальдо із першої таблиці дорівнюють індивідуальним сальдо із другої. - Вікно "Поиска решения" зображено на рисунку 2.9.
Рис. 2.9 – Вікно «Поиска решения» для моделі взаємозаліку боргів підприємства
Після проведення розрахунків було отримано наступні значення (Рис.2.10).
Рис. 2.10 – Результати задачі взаємозаліку боргів підприємства Висновок Таким чином, після перерозподілення боргів підприємства сальдо кожного виробництва залишилось незмінним. До перерозподілу сума боргів становила 4950,00 ум.од., а після застосування моделі зменшилась більше, ніж в 2 рази, і в свою чергу становить 1382,01 ум.од. Постановка задачі На 3-х верстатах виготовляється 5 деталей (деталь №5 завжди після деталі №3), а послідовність оброблення інших деталей не має значення; тривалість оброблення деталей на верстатах задана в таблиці; розробити таблицю варіантів оброблення і визначити оптимальний план за трьома критеріями: найшвидше закінчення робіт, найменша тривалість простоїв верстатів, найменший час перебування деталей в процесі виробництва. Початкові дані наведені в таблиці 2.3. Таблиця 2.3 – Початкові дані для задачі визначення оптимальної послідовності виготовлення деталей
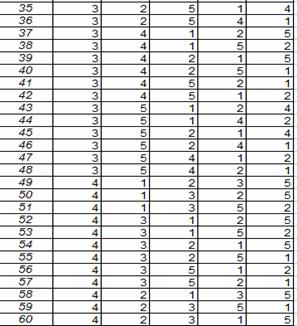
Методика реалізації моделі Перша таблиця – це таблиця початкових даних (таблиця 2.3). Ця таблиця має розмірність 5х3 (оскільки в задачі розглядаються 5 деталей та 3 верстати). Значеннями даної таблиці є тривалість обробки кожної деталі на кожному верстаті.
2. Наступна таблиця – це таблиця варіантів обробки деталей (таблиця 2.4).
Таблиця 2.4 – Таблиця варіантів обробки деталей
3. Створюємо таблицю тривалості обробки деталей. Рядки відповідають трьом верстатам, а стовпчику – п'ятьом деталям. Нижчк цієї таблиці запишемо рядок, який визначає варіант послідовності обробки деталей. Елементи таблиці заповнюються на основі цього варіанту та елементів першої таблиці за допомогою функції ВПР. Ця функція містить чотири параметри. Перший параметр – це адреса відповідної клітинки рядка, що визначає варіант послідовності обробки деталей. Другий параметр – це перша таблиця. Третій параметр визначає стовпчик першої таблиці, який відповідає верстатові (2,3 або 4). Четвертий параметр – логічне значення ЛОЖЬ. Таблиця 2.5 – Тривалість обробки деталей
4. Таблиця початок роботи з деталями на верстатах (таблиця 2.6) заповнюється за такими правилами: 1) лівий верхній елемент дорівнює «0»; 2) елементи першого рядка дорівнюють елементам, що стоять зліва від даного + відповідний елемент із першої таблиці; 3) елементи першого стовпчика дорівнюють елементам, що стоять вище від даного + відповідний елемент із першої таблиці; 4) інші елементи визначаються через функцію МАКС (параметри цієї функції вибираються із 3-ї таблиці зліва та вище відповідного елементу). Таблиця 2.6 – Початок оброблення деталей
5. Таблиця завершення роботи з деталями на верстаті заповнюється додаванням відповідних елементів таблиці тривалості й таблиці початків робіт. Таблиця 2.7 – Завершення оброблення деталей
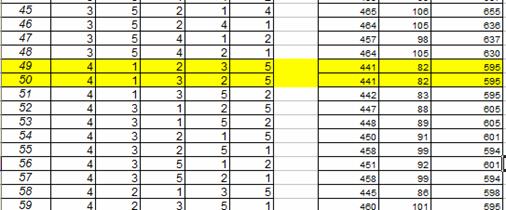
6. Для вибраної послідовності обробки необхідно визначити 3 критерії: 1) найшвидше закінчення робіт (правий нижній елемент 3-ї таблиці); 2) простої верстатів (сума елементів 4-го стовпця 3-ї таблиці мінус сума всіх елементів 1-ї таблиці); 3) найменший час перебування деталей в процесі виробництва (сума елементів 3-го рядка 3-ї таблиці). 7. Для визначення оптимального плану необхідно перевірити всі 60 комбінацій порядку обробки деталей. Для кожного варіанту визначаємо значення критеріїв. 8. Вибираємо із варіантів оптимальні за вказаними критеріями (Рис. 2.8)
Рис. 2.8 – Вибір оптимального варіанту
Висновок Після проведення обрахунків ми можемо вибрати оптимальний план по виготовленню деталей і мінімізувати простої верстатів, що призведе до більшої продуктивності. Всі необхідні умови забезпечують варіанти 49 і 50. Найшвидше закінчення робіт має значення 441 ум. од., час перебування деталей в процесі виробництва становить 595 ум.од., а простої - 82 ум. од. Ці значення є мінімальними із всіх можливих, саме тому максимально збільшують продуктивність роботи та прибуток від виробництва. Висновок Під час вивчення курсу «моделювання економіки» я отримали навики з вирішення задач за допомогою методу математичного моделювання і закріпила знання під час виконання курсової роботи. Я впевнилися, що вибір ефективних управлінських рішень неможливий без всебічного аналізу комплексу взаємозалежних чинників, визначення і порівняльної оцінки можливих альтернатив і допустимих планів дій. З розвитком суспільства, економіки та ринкових відносин посилюється відповідальність суб’єкта управління за визначення правильних управлінських рішень щодо належного керування об’єктом управління – суб’єктом економічної діяльності. Тому я вважаю, що економіко-математичне моделювання швидкий, зручний та багатофункціональний метод, що є невід’ємною частиною процесу прийняття управлінських економічних рішень. А підприємство, яке зацікавлене в отриманні результативної роботи, повинне обов’язково мати економістів-програмістів, які зможуть забезпечити відмінне функціонування одного із найбільш динамічних розділів прикладної економічної науки Література: 1) Вітлінський В. В. Моделювання економіки. Навчальний посібник. –К.: КНЕУ, 2003. — 408 с. 2) Кігель В.Р. Математичні методи ринкової економіки: навч.посібник / В.Р. Кігель. – К.: Кондор, 2003. – 158с. 3) Федосеев В.В. Экономико-математические методы и прикладные модели / В.В. Федосеев, А.Н. Гармаш, Д.М. Даитбегов и др. – М.: ЮНИТИ, 1999.- 391с. 4) Шелобаев С. И. Математические методы и модели в экономике, финансах, бизнесе. Учебное пособие для вузов – М.: ЮНИТИ, ДАНА, 2000. — 367 с.
Зміст Вступ. 4 Розділ 1: «Використання математичних моделей для обґрунтування управлінських рішень в ситуації ризику». 5 1.1 Поняття моделі 5 1.2 Прийняття рішень в умовах ризику. 7 1.3 Приклади математичних моделей в ситуації ризику. 7 1.3.1 Задача оптимального управління портфелем фінансових активів. 7 1.3.2. Задача оптимізації валютного резерву. 11 1.3.3. Оптимізація кредитного портфеля. 13 Розділ 2: «Розв'язок економічних задач». 17 2.1 Оптимальне перевезення вантажів. 17 Постановка задачі 17 Економіко-математична модель задачі 17 Методика реалізації моделі 18 Висновок. 20 2.2 Оптимізація порожнього пробігу автотранспорту. 20 Постановка задачі 20 Економіко-математична модель задачі 21 Методика реалізації моделі 22 Висновок. 24 2.3 Взаємозалік боргів підприємства. 24 Постановка задачі 24 Економіко-математична модель задачі 25 Методика реалізації моделі 25 Висновок. 28 2.3 Визначення оптимальної послідовності виготовлення деталей. 28 Постановка задачі 28 Економіко-математична модель задачі 29 Методика реалізації моделі 30 Висновок. 34 Висновок. 35 Література: 36
Вступ На сучасному етапі розвитку науки і техніки в усіх галузях людської діяльності знаходять широке застосування методи моделювання економіки. Тому важливого значення набуває використання економічно-математичних методів і моделей у практичній діяльності. Важливою є умова та особливості їх застосування залежно від мети дослідження, прийнятої системи гіпотез. Основним інструментальним та ефективним методом дослідження систем є метод моделювання, тобто спосіб теоретичних і практичних дій, спрямованих на створення та використання моделей. Під моделлю можна розуміти образ реального об’єкта (процесу) в матеріальній чи ідеальній формі (тобто такий, який описано знаковими засобами певною мовою), що відображає суттєві властивості модельованого об’єкта (процесу) й заміщує його в ході дослідження й управління. Метод моделювання ґрунтується на принципі аналогії, тобто можливостях вивчення реального об’єкта не безпосередньо, а шляхом дослідження подібного йому й більш доступного цьому дослідженню об’єкта – його моделі. Мета курсової – навчитися застосовувати методологію, методику та інструментарій економіко-математичного моделювання в теоретичних дослідженнях та використовувати здобуті знання у практичній діяльності. Для досягнення мети поставлені наступні задачі: 1) Визначити оптимальний план перевезення вантажів; 2) Оптимізувати порожній пробіг автотранспорту; 3) Перерозподілити борги підприємства; 4) Визначити оптимальну послідовність обробки деталей на верстатах за критеріями: a. критерій найшвидшого закінчення робіт; b. критерій мінімізації перебування деталей в процесі виробництва; c. критерій мінімізації простоїв верстав. Розділ 1: «Використання математичних моделей для обґрунтування управлінських рішень в ситуації ризику» Поняття моделі Термін «модель» походить від латинського слова «modulus» — зразок, норма, міра. Модель — це об’єкт, що заміщує оригінал і відбиває найважливіші риси і властивості оригіналу для даного дослідження, даної мети дослідження за обраної системи гіпотез. Математична модель — це абстракція реальної дійсності (світу), в якій відношення між реальними елементами, а саме ті, що цікавлять дослідника, замінені відношеннями між математичними категоріями. Ці відношення зазвичай подаються у формі рівнянь і/чи нерівностей, відношеннями формальної логіки між показниками (змінними), які характеризують функціонування реальної системи, що моделюється. Сутність цієї методології полягає в заміні вихідного об’єкта його «образом» — математичною моделлю — і подальшим вивченням (дослідженням) моделі на підставі аналітичних методів та обчислювально-логічних алгоритмів, які реалізуються за допомогою комп’ютерних програм. Робота не із самим об’єктом (явищем, процесом), а з його моделлю дає можливість відносно швидко і безболісно досліджувати його основні (суттєві) властивості та поводження за будь-яких імовірних ситуацій (це переваги теорії). Водночас обчислювальні (комп’ютерні, симулятивні, імітаційні) експерименти з моделями об’єктів дозволяють, спираючись на потужність сучасних математичних та обчислювальних методів і технічного інструментарію інформатики, ретельно та досить глибоко вивчати об’єкт у достатньо детальному вигляді, що недоступно суто теоретичним підходам (це перевага експерименту). Не дивно, що методологія математичного моделювання бурхливо розвивається, охоплюючи аналіз надзвичайно складних економічних і соціальних процесів. Технічні, технологічні, економічні, політичні та інші системи, що їх вивчає сучасна наука, все меншою мірою піддаються дослідженню (в необхідній комплексності та точності) звичайними теоретичними методами, хоча останні є надзвичайно важливими. Безпосередній натурний експеримент над ними є надто тривалим, дорогим, часто навіть небезпечним чи просто неможливим, особливо це стосується економічних систем і процесів. Тому математичне моделювання є неминучою складовою науково-технічного прогресу.
Рис. 1.1. Узагальнена схема математичного моделювання Створивши тріаду: «модель—алгоритм—програма», дослідник (системний аналітик) отримує універсальний, гнучкий і відносно дешевий інструмент, який тестується в «пробних» обчислювальних експериментах. Після того як адекватність (достатній рівень відповідності, зважаючи на цілі та взяту систему гіпотез) тріади щодо вихідного об’єкта засвідчена, з моделлю проводять різноманітні та детальні «досліди», які дають нову інформацію про необхідні якісні та кількісні властивості й характеристики об’єкта. Процес моделювання супроводжується поліпшенням та уточненням, за необхідності, всіх складових (ланок) тріади. Якщо ж аналізувати проблеми моделювання економічних систем, де необхідно брати до уваги «людський чинник», тобто коли йдеться про аналіз слабоформалізованих об’єктів, то до цих вимог необхідно додати ще низку, зокрема, акуратне розмежування математичних і побутових термінів, завбачливе застосування вже готового математичного апарату до вивчення явищ і процесів (пріоритетним є шлях «від задачі до методу», а не навпаки) та інші.
|
||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 485; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.017 с.) |


 .
. і визначається як середнє значення квадрату різниці:
і визначається як середнє значення квадрату різниці:
 .
.







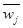 – математичне сподівання;
– математичне сподівання;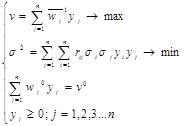

 і
і  ті межі для середнього значення й дисперсії, які одержані від особи, що приймає рішення. Ці межі можуть бути реальними або нереальними. Наше завдання: якщо ці межі реальні – то визначити можливість їх покращення, якщо ж вони нереальні – то ми повинні їх скоригувати так, щоб вони стали реальними, але найближчими до особи, що приймає рішення, а потім розв’язати задачу і передати оптимальний план на затвердження.
ті межі для середнього значення й дисперсії, які одержані від особи, що приймає рішення. Ці межі можуть бути реальними або нереальними. Наше завдання: якщо ці межі реальні – то визначити можливість їх покращення, якщо ж вони нереальні – то ми повинні їх скоригувати так, щоб вони стали реальними, але найближчими до особи, що приймає рішення, а потім розв’язати задачу і передати оптимальний план на затвердження.









 .
. .
. .
.