Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оптимізація порожнього пробігу автотранспортуСодержание книги Поиск на нашем сайте
Постановка задачі Споживачам потрібні вантажі, які зосереджені в різних постачальників, перевезення здійснюється автотранспортом одного типу, після розвантаження у споживача автомобіль повертається за вантажем до постачальника, але не обов'язково до попереднього; для кожного постачальника відомо, яку кількість вантажу до якого споживача потрібно перевезти (кількість вантажу дорівнює кількості рейсів). Скласти план перевезень, щоб загальний порожній пробіг автомобілів був найменшим. Початкові дані зображено на рисунку 2.4.
Рис. 2.4 – Початкові дані для задачі оптимізації порожнього пробігу Економіко-математична модель задачі Параметри: m – кількість постачальників; n – кількість споживачів; xij – кількість рейсів, що необхідно зробити від і-того постачальника до j-того споживача. Ці величини вважаються відомими; bj – кількість рейсів, зроблених протягом зміни до j-того споживача;
ai – кількість рейсів, що потрібно зробити для вивезення вантажів від і-того постачальника;
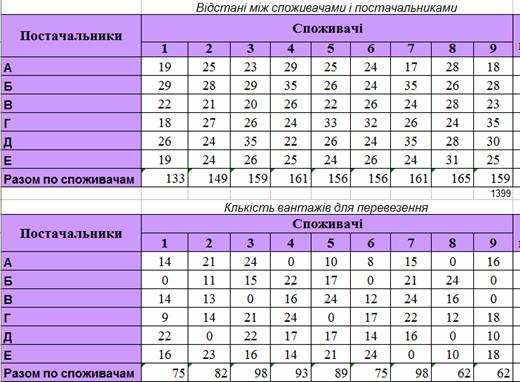
lij – відстані від і-того постачальника до j-того споживача; vij – кількість рейсів до і-того постачальника від j-того споживача. Тоді обмеження мають вигляд:
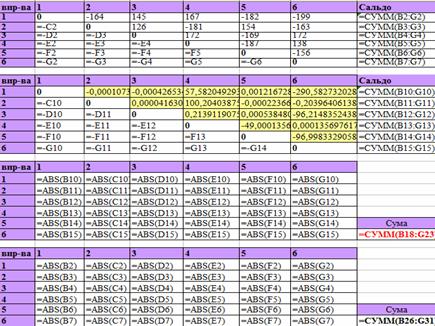
Методика реалізації моделі У першій таблиці запишемо відстані від постачальників до споживачів. У другій таблиці вкажемо кількість рейсів, які потрібно зробити від постачальників до споживачів. У цій же таблиці визначаємо загальну кількість рейсів для постачальників і споживачів. У третій таблиці визначаємо кількість порожніх рейсів від споживачів до постачальників. На початку вони приймають значення 0. Визначаємо загальну кількість цих рейсів за порядками. У четвертій таблиці визначаємо порожній пробіг. Для цього відстані між постачальниками і споживачами множимо на кількість рейсів (тобто, елементи першої таблиці множимо на відповідні елементи третьої). Формули для розрахунків зображені на рисунку 2.5.
Рис. 2.5 – Формули для моделі оптимізації порожнього пробігу автотранспорту Визначаємо загальний порожній пробіг за порядками і стовпчиками та загальний порожній пробіг за всією таблицею. Цей пробіг є цільової клітиною "Поиска решения" і приймає найменше значення. Змінними є клітинки третьої таблиці.
Обмеження: 1) елементи третьої таблиці є цілими та невід'ємними; 2) кількість рейсів від постачальника дорівнює кількості порожніх рейсів до постачальника; 3) кількість рейсів до споживача дорівнює кількості порожніх рейсів від споживача.
Вікно "Поиска решения" зображено на рисунку 2.6.
Рис. 2.6 – Вікно «Поиска решения» для моделі оптимізації порожнього пробігу автотранспорту Отримані результати зображено на рисунку 2.7.
Рис. 2.7 – Результати задачі оптимізації порожнього пробігу автотранспорту Висновок Отже, після проведення обчислень можна сказати, що найбільшу кількість порожніх рейсів зробив постачальник Е, а найменше - постачальник А, відповідно 140 та 107. За умовою задачі потрібно було скласти такий план перевезень, щоб загальний порожній пробіг автомобілів був найменшим, у даному випадку він дорівнює 15 922 км. Взаємозалік боргів підприємства Постановка задачі Деяке підприємство складається з кількох видів виробництв, які заборгували один одному кошти, потрібно перерозподілити борги так, щоб сума всіх взаємних боргів була найменшою, а сальдо кожного виробництва не змінилося. Початкові дані наведені в таблиці 2.2. Таблиця 2.2 – Початкові дані для задачі взаємозаліку боргів підприємства
Економіко-математична модель задачі Параметри моделі N – кількість підприємств
Обмеження моделі:
Критерій моделі:
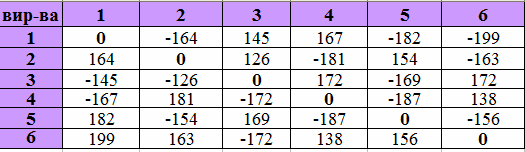
Методика реалізації моделі Взаємні заборгованості підприємств запишемо в таблицю. Кількість рядків таблиці дорівнює кількості стовпчиків та кількості підприємств. На перетині i-го рядка і j-го стовпчика запишемо борг і-го підприємства j-му. Якщо цей борг від'ємний, то і-те підприємство віддає борг j-му; якщо додатний – навпаки. По головній діагоналі таблиці з лівого верхнього кута в правий нижній пишемо 0. Вище діагоналі запишемо довільні початкові дані, а нижче діагоналі запишемо вираз:
Для даної таблиці визначаємо суми за рядками – це сальдо Друга таблиця, такої ж розмірності, як і перша, призначена для одержання оптимального рішення. По головній діагоналі пишемо 0, вище неї – також 0. Нижче записуємо вираз, який забезпечує рівність:
Для даної таблиці теж визначаємо сальдо. Третя таблиця містить абсолютні величини значень другої таблиці (функція ABS()).Визначаємо суму елементів цієї таблиці – це оптимальне значення критерію. Четверта таблиця включає абсолютні елементів першої таблиці. Вона необхідна для порівняння поточного та оптимального станів заборгованості. Формули для розрахунків зображені на рисунку 2.8.
Рис. 2.8 – Формули для моделі взаємозаліку боргів підприємства
Цільовою клітинкою для "Поиска решения" – сума всіх елементів третьої таблиці, вона повинна прийняти мінімальне значення. Змінними клітинками являються клітинки другої таблиці вище головної діагоналі. Обмеження: - індивідуальні сальдо із першої таблиці дорівнюють індивідуальним сальдо із другої. - Вікно "Поиска решения" зображено на рисунку 2.9.
Рис. 2.9 – Вікно «Поиска решения» для моделі взаємозаліку боргів підприємства
Після проведення розрахунків було отримано наступні значення (Рис.2.10).
Рис. 2.10 – Результати задачі взаємозаліку боргів підприємства Висновок Таким чином, після перерозподілення боргів підприємства сальдо кожного виробництва залишилось незмінним. До перерозподілу сума боргів становила 4950,00 ум.од., а після застосування моделі зменшилась більше, ніж в 2 рази, і в свою чергу становить 1382,01 ум.од.
|
||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 244; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.36.89 (0.01 с.) |

 ;
; ;
;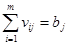 ;
;  ;
;  ;
; .
.


 – борг і-го підприємства j-му. Якщо цей борг від'ємний, то і-те підприємство віддає борг j-му; якщо додатне – навпаки.
– борг і-го підприємства j-му. Якщо цей борг від'ємний, то і-те підприємство віддає борг j-му; якщо додатне – навпаки. – борг і-го підприємства j-му, який залишається після перерозподілу. Це керовані змінні, їх значення визначаються під час розв’язку задачі.
– борг і-го підприємства j-му, який залишається після перерозподілу. Це керовані змінні, їх значення визначаються під час розв’язку задачі. – сальдо кредитів і боргів підприємства
– сальдо кредитів і боргів підприємства ;
; ;
; .
. .
. .
.