
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оптимізація кредитного портфеляСодержание книги Поиск на нашем сайте
Є кілька позичальників, які бажають взяти банківський кредит. Для кожного позичальника банк розробляє графік повернення кредиту, який включає дати повернення та розміри платежів. Загальна сума всіх платежів повинна забезпечити повернення кредиту разом з відсотками. Загальна кількість коштів для кредитування обмежена (визначається довільно). Визначити, яким позичальникам виділити кредити, щоб одержати найбільший прибуток. Задачу розв'язати для варіанту, коли повернення кредиту всіма позичальниками гарантовано, і для варіанту, коли можливі не повернення кредитів. Керовані змінні в цій задачі приймають тільки два значення: 0 або 1. Вважається, що загальні кошти, які можна використати для кредитування обмежені. Вид моделі, коли повернення кредиту всіма позичальниками гарантовано Для побудови моделі спочатку визначимо який прибуток одержить банк від кредиту якщо цей кредит буде повернутий. Позначення: Q – розмір позики; T0 – час видачі позики. Розглянемо графік платежів: Vi – величини платежів; Ti – час платежів. Прибуток банку визначається рівністю:
ri – ставка дисконту для моменту часу Ti.
r – нормативна добова кредитна ставка. Вид моделі, коли можливі не повернення кредитів У цій ситуації для кожного позичальника вважається відомою імовірність Pi неповернення ним кредиту. Для кожного позичальника можна визначити математичне сподівання та дисперсію одержаного в банку продукту. Математичне сподівання:
Дисперсія:
Далі визначаємо коефіцієнти rij між платоспроможними постачальниками, а потім математичне сподівання і дисперсію загального прибутку банка. Нехай є n кредитних запитів. Кредитний портфель визначається набором чисел х1, х2, х3,..., хn, які рівні 0 або 1 і визначають чи надається кредит за даним запитом. Для кожного позичальника визначається імовірність Pi – неповернення ним кредиту. На основі цієї імовірності визначається середнє значення прибутку від даного кредиту і визначається дисперсія:
Di – прибуток від кредиту, якщо цей кредит повертається згідно графіка; Qi – величина кредиту; Pi – імовірність неповернення. Загальними показниками кредитного портфеля є середнє значення та дисперсія загального прибутку від усіх кредитів. Він визначається рівністю:
ρij – коефіцієнти кореляції між і -тим та j -тим кредитом. Задача має такий вигляд:
Обмеження:
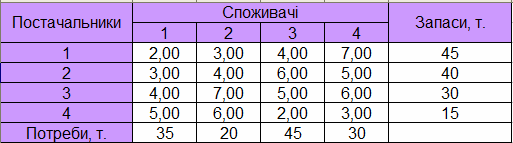
хі = 0 або 1. k – коефіцієнт, який показує несхильність до ризику. Чим більший коефіцієнт k, тим більш несхильною до ризику є кредитна політика банку. Орієнтованими значеннями k є такі: 0,02 – помірний рівень; 0,05 – середній рівень; 0,1 – високий рівень. Розділ 2: «Розв'язок економічних задач» Оптимальне перевезення вантажів Постановка задачі Із 4 складів в 4 крамниці потрібно перевезти борошно. Відомі запаси борошна на кожному складі, потреби крамниць і вартість перевезення 1т борошна з кожного складу в кожну крамницю. Визначити такий план перевезень, щоб сумарна вартість перевезення була мінімальною, борошно все вивезене, а потреби крамниць задоволені. Розглядається закрита модель, за якою запаси постачальників дорівнюють потребам споживачів. Початкові дані наведені в таблиці 2.1. Таблиця 2.1 – Початкові дані
Економіко-математична модель задачі Основною задачею на оптимізацію перевезень є транспортна задача. Параметри: m – кількість постачальників; n – кількість споживачів; ai – запаси для i-того постачальника; bj – потреби j-того споживача; dij – вартості перевезень одиниці вантажу від i-того постачальника до j-того споживача; xij – кількість вантажу, який перевозиться від і-того постачальника до j-того споживача (керовані параметри). Потрібно скласти план перевезень, для якого загальна вартість всіх перевезень є найменшою. Обмеження та критерій моделі
У даній постановці задачі вважається, що загальний запас всіх постачальників дорівнює загальній потребі всіх споживачів: Методика реалізації моделі Після створення таблиці початкових даних, у другу таблицю запишемо кількості перевезених вантажів від кожного постачальника до кожного споживача. На початку ці величини приймаємо рівними 0. Нижній рядок і крайній правий стовпець цієї таблиці відводимо для запису загальної кількості вантажів, які перевезені від кожного постачальника до кожного споживача (суми по рядках і стовбцях). Третя таблиця визначає вартість перевезень. В її клітинки запишемо добутки кількості вантажу з другої таблиці на вартість перевезення одиниці вантажу з першої. Нижній рядок відводимо для загальної вартості перевезень до кожного споживача, сума по стовбцям (Рис. 2.1). Загальна вартість усіх перевезень визначається як сума значень цього рядка. Клітинка загальної вартості вибирається як цільова в "Поиске решения". Змінними клітинками є кількість вантажу, який перевозиться від і-того постачальника до j-того споживача. Обмеження: 1) загальна кількість перевезень до кожного споживача дорівнюють його потребам; 2) загальна кількість перевезень від кожного постачальника дорівнюють його запасам; 3) всі перевезення невід’ємні та є цілими числами; 4) всі перевезення не перевищують загальних запасів.
Рис. 2.1 – Формули для моделі оптимального перевезення вантажів Вікно "Поиска решения" зображено на рисунку 2.2.
Рис. 2.2 – Вікно "Поиска решения" для моделі оптимального перевезення вантажів Після проведення обчислень було отримано наступні результати (Рис. 2.3).
Рис. 2.3 – Результати задачі оптимального перевезення вантажів Висновок Так як, за умовою задачі модель збалансована, то потреби крамниць були задоволені, а все борошно вивезене. Так 1-ий постачальник задовольнив потреби 1 та 2 крамниць, 2-й постачальник – 1, 2 та 4 крамниць, 3-й та 4-й постачальник задовольнили потреби 3-ї крамниці. У результаті було визначено оптимальний план перевезень, сумарна мінімальна вартість при якому становить 470 ум. од.
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 270; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.195.153 (0.007 с.) |







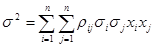

 ;
;
 ;
; ;
; ;
; ;
; .
.





