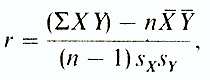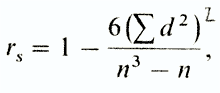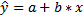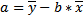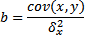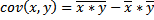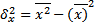Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистика численности населения.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Статистика численности населения. Расчет среднегодовой численности населения. Для расчета ряда показателей необходимо знать среднюю за период численность населения. Среднюю численность населения можно рассчитать различными методами. 1) Средняя арифметическая Если известна численность населения на начало и конец года, то средняя годовая численность населения рассчитывается как средняя арифметическая из этих двух чисел.
где, Н1 и Н2 — численность населения на начало и конец периода. 2) Простая хронологическая средняя
Если интервалы между наблюдениями расположены через равные промежутки времени — то формуле простой хронологической средней:
Где Н1, Н2, Нn-1 и Hn — численность населения на каждую дату. 3) Хронологическая взвешенная В случае если замеры численности населения проводились через неравные промежутки времени то — по формуле хронологической взвешенной:
где: Hi - полусумма двух соседних уровней ряда динамики; ti — промежуток между двумя уровнями ряда, выраженный в днях, неделях или месяцах.
Расчет коэффициента общего прироста населения. Коэффициент общего прироста населения = Коэффициент общей интенсивности миграции населения (миграционного прироста) + Коэффициент естественного прироста (изменения) населения Расчет будущей численности населения. Перспективная общая численность населения рассчитывается на основе данных о естественном и механическом приросте населения за определенный анализируемый период и предположении о сохранении выявленной закономерности на прогнозируемый отрезок времени.
где Sн — численность населения на начало планируемого периода; t — число лет, на которое прогнозируется расчет; Кобщ.пр.— коэффициент общего прироста населения за период, предшествующий плановому. Показатели статистики производства материальных благ и услуг. Промышленная продукция. Определения. Промышленная продукция - это прямой полезный результат промышленно-производственной деятельности фирмы (предприятия), выраженный в форме продуктов (изделий), либо производственных услуг. Однако закупленное сырье, материальные ресурсы, из которых изготавливается продукция, не могут включаться в состав продукции данного предприятия, так как они добыты или произведены на других предприятиях. С другой стороны промышленная продукция - это результат основной промышленной деятельности. Поэтому к промышленной продукции не относится продукция непромышленных, хоть и производственных подразделений предприятия, например, транспортного, строительного, энергетического цехов или сельскохозяйственного подразделения. Промышленная продукция как результат промышленной деятельности может выступать в нескольких видах: основная; побочная; сопряженная. Основная продукция - это результат деятельности предприятия без учета отходов. Продукция, которая выпускается вместе с основной и имеет самостоятельную ценность, называется побочной. Если при производстве из одного вида сырья одновременно получают несколько видов изделий, то такую продукцию называют сопряженной. При статистическом учете по степени готовности различают такие типы промышленной продукции: · готовые изделия, которые произведены на данном предприятии и не нуждаются в последующей обработке в его границах; · полуфабрикаты - это изделия, обработка которых закончена в одних подразделениях предприятия и подлежит последующей обработке в других подразделениях того же предприятия; · незавершенное производство - это продукция, обработка которой в пределах данного подразделения предприятия не закончена. Выпущенная продукция выступает также в формах рыночных и нерыночных услуг. Расчет валового оборота. Валовой оборот включает готовую продукцию, незавершенное производство, внутренний оборот предприятия, выполнение работ производственного характера. Расчет ВП, исходя из ВО Валовая продукция (ВП) является основным показателем объема производства промышленного предприятия, которая в стоимостном выражении рассчитывается по формуле: ВП = ВО-ВЗО, где ВО - это валовой оборот, который характеризует стоимость всего объема совокупной продукции предприятия (готовых изделий и полуфабрикатов) независимо от их последующего назначения; ВЗО - внутризаводской оборот, который показывает стоимость полуфабрикатов собственной выработки. Индекс номинальной з/п. Индекс номинальной заработной платы (в денежной форме) отражает изменение ее уровня за отчетный период по сравнению с базисным периодом. Индекс реальной заработной платы (воплощенной в массе жизненных благ, которые можно приобрести за номинальную зарплату) характеризует изменение покупательной способности номинальной зарплаты за отчетный период по сравнению с базисным. Индекс номинальной заработной платы определяют сравнение уровня средней заработной платы (часовая, дневная месячная, квартальная, годовая) за различные периоды времени или делением индекса фонда заработной платы на индекс количества работников (или на индекс отработанного времени). Индекс номинальной заработной платы характеризует изменение заработной платы в денежной форме независимо от покупательной способности национальной денежной единицы Индекс реальной з/п. Для определения индекса реальной заработной платы вычисляется индекс номинальной заработной платы, средний индекс цен на товары, которые покупают рабочие и служащие, средний индекс цен на услуги, которые оплачивают рабочие и служащие из заработной платы, средний индекс цен на все товары и услуги, приобретенные рабочими и служащими, учитывая удельный вес каждой статьи из этих расходов в общей сумме их зарплаты, и определяют его делением индекса номинальной заработной платы на индекс цен на товары и услуги.
Статистика рынка труда Баланс трудовых ресурсов Балансом трудовых ресурсов (БТР) называется система показателей, отражающих численность и состав трудовых ресурсов, и их распределение на занятых по отраслям экономики и формам собственности, безработных и экономически неактивное население. Баланс трудовых ресурсов может быть составлен: по стране в целом; по отдельным субъектам РФ; краям и областям с распределением на городскую и сельскую местность.
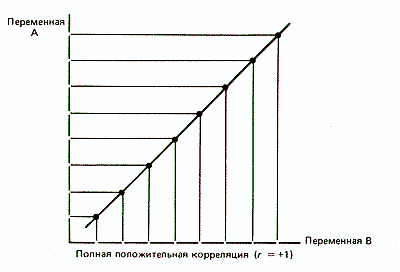
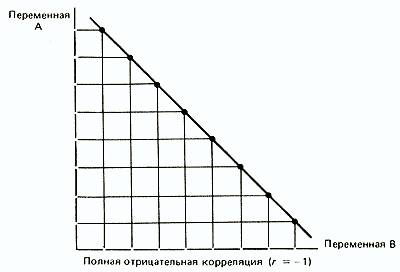
Корреляционный анализ При изучении корреляций стараются установить, существует ли какая-то связь между двумя показателями в одной выборке (например, между ростом и весом детей или между уровнем IQ и школьной успеваемостью) либо между двумя различными выборками (например, при сравнении пар близнецов), и если эта связь существует, то сопровождается ли увеличение одного показателя возрастанием (положительная корреляция) или уменьшением (отрицательная корреляция) другого. Иными словами, корреляционный анализ помогает установить, можно ли предсказывать возможные значения одного показателя, зная величину другого. До сих пор при анализе результатов нашего опыта по изучению действия марихуаны мы сознательно игнорировали такой показатель, как время реакции. Между тем было бы интересно проверить, существует ли связь между эффективностью реакций и их быстротой. Это позволило бы, например, утверждать, что чем человек медлительнее, тем точнее и эффективнее будут его действия и наоборот. С этой целью можно использовать два разных способа: параметрический метод расчета коэффициента Браве-Пирсона (r) и вычисление коэффициента корреляции рангов Спирмена (rs), который применяется к порядковым данным, т.е. является непараметрическим. Однако разберемся сначала в том, что такое коэффициент корреляции. Коэффициент корреляции Коэффициент корреляции — это величина, которая может варьировать в пределах от +1 до -1. В случае полной положительной корреляции этот коэффициент равен плюс 1, а при полной отрицательной — минус 1. На графике этому соответствует прямая линия, проходящая через точки пересечения значений каждой пары данных:
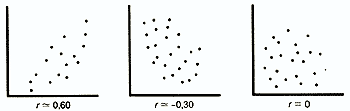
В случае же если эти точки не выстраиваются по прямой линии, а образуют «облако», коэффициент корреляции по абсолютной величине становится меньше единицы и по мере округления этого облака приближается к нулю:
В случае если коэффициент корреляции равен 0, обе переменные полностью независимы друг от друга. В гуманитарных науках корреляция считается сильной, если ее коэффициент выше 0,60; если же он превышает 0,90, то корреляция считается очень сильной. Однако для того, чтобы можно было делать выводы о связях между переменными, большое значение имеет объем выборки: чем выборка больше, тем достовернее величина полученного коэффициента корреляции. Существуют таблицы с критическими значениями коэффициента корреляции Браве-Пирсона и Спирмена для разного числа степеней свободы (оно равно числу пар за вычетом 2, т. е. n- 2). Лишь в том случае, если коэффициенты корреляции больше этих критических значений, они могут считаться достоверными. Так, для того чтобы коэффициент корреляции 0,70 был достоверным, в анализ должно быть взято не меньше 8 пар данных ( h =n -2=6) при вычислении r (см. табл. 4 в Приложении) и 7 пар данных (h= n-2= 5) при вычислении rs (табл. 5 в Приложении). Хотелось бы еще раз подчеркнуть, что сущность этих двух коэффициентов несколько различна. Отрицательный коэффициент r указывает на то, что эффективность чаще всего тем выше, чем время реакции меньше, тогда как при вычислении коэффициента rsтребовалось проверить, всегда ли более быстрые испытуемые реагируют более точно, а более медленные — менее точно. Коэффициент корреляции Браве-Пирсона (r) — этопараметрический показатель, для вычисления которого сравнивают средние и стандартные отклонения результатов двух измерений. При этом используют формулу (у разных авторов она может выглядеть по-разному)
где Σ XY — сумма произведений данных из каждой пары; Коэффициент корреляции рангов Спирмена ( rs ) — это непараметрический показатель, с помощью которого пытаются выявить связь между рангами соответственных величин в двух рядах измерений. Этот коэффициент рассчитывать проще, однако результаты получаются менее точными, чем при использовании r. Это связано с тем, что при вычислении коэффициента Спирмена используют порядок следования данных, а не их количественные характеристики и интервалы между классами. Дело в том, что при использовании коэффициента корреляции рангов Спирмена (rs) проверяют только, будет ли ранжирование данных для какой-либо выборки таким же, как и в ряду других данных для этой выборки, попарно связанных с первыми (например, будут ли одинаково «ранжироваться» студенты при прохождении ими как психологии, так и математики, или даже при двух разных преподавателях психологии?). Если коэффициент близок к +1, то это означает, что оба ряда практически совпадают, а если этот коэффициент близок к -1, можно говорить о полной обратной зависимости. Коэффициент rs вычисляют по формуле
где d — разность между рангами сопряженных значений признаков (независимо от ее знака), а — число пар. Обычно этот непараметрический тест используется в тех случаях, когда нужно сделать какие-то выводы не столько об интервалах между данными, сколько об их рангах, а также тогда, когда кривые распределения слишком асимметричны и не позволяют использовать такие параметрические критерии, как коэффициент r (в этих случаях бывает необходимо превратить количественные данные в порядковые).
_____________________________________________________________________
Линейное уравнение парной регрессии имеет вид: _________________________________________________________ Алгоритм расчета коэффициентов парной линейной регрессии
у результативный признак, или зависимый cov – ковариация _________________________________________________________________ Статистика численности населения.
|
||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 3206; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.007 с.) |

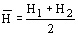
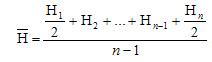
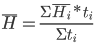
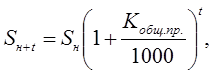 Если известна численность населения на начало какого-то периода и рассчитан коэффициент общего прироста населения (Кобщ.пр. = Крод. - Ксм. + Кмех.пр.), то перспективная численность населения через t лет:
Если известна численность населения на начало какого-то периода и рассчитан коэффициент общего прироста населения (Кобщ.пр. = Крод. - Ксм. + Кмех.пр.), то перспективная численность населения через t лет: