
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
На специальности «лечебное дело»Содержание книги Поиск на нашем сайте
МЕТОДИЧЕСКАЯ РАЗРАБОТКА ПРАКТИЧЕСКОГО ЗАНЯТИЯ ДЛЯ СТУДЕНТОВ, ОБУЧАЮЩИХСЯ НА СПЕЦИАЛЬНОСТИ «ЛЕЧЕБНОЕ ДЕЛО» ПО ТЕМЕ: «СТАТИСТИЧЕСКАЯ СОВОКУПНОСТЬ. ВЫЧИСЛЕНИЕ ОТНОСИТЕЛЬНЫХ ВЕЛИЧИН ТИПОВОЕ ЗАДАНИЕ На основе приведенных в таблице данных: 1. Вычислить интенсивные (повозрастную и общую плодовитость) и экстенсивные показатели (распределение живорожденных по возрасту матери). 2. Свести полученные показатели в таблицу. 3. Изобразить графически относительные величины. 4. На основе анализа полученных показателей сделать соответствующие выводы.
Повозрастная численность женщин детородного возраста города М. и число живорожденных в каждой возрастной группе:
ОБРАЗЕЦ ВЫПОЛНЕНИЯ ЗАДАНИЯ I. Интенсивный показатель – это показатель частоты, отражает определенную закономерность распространенности явлений в общей среде, отношение явления к общей среде.
интенсивный показатель = 1.Плодовитость женщин в возрасте до 20 лет:
2.Плодовитость женщин в возрасте 20-24 лет:
3.Плодовитость женщин в возрасте 25-29 лет:
4.Плодовитость женщин в возрасте 30-34 лет:
5.Плодовитость женщин в возрасте 35-39 лет:
6.Плодовитость женщин в возрасте 40-44 лет:
7.Плодовитость женщин в возрасте 45-49 лет:
8.Общая плодовитость женщин:
II. Экстенсивный показатель – относительный показатель, характеризующий распределение явления внутри одной совокупности, указывает какую долю занимает данное явление в общей совокупности.
экстенсивный показатель =
1. Удельный вес живорожденных, родившихся у женщин в возрасте до 20 лет:
2. Удельный вес живорожденных, родившихся у женщин в возрасте 20-24 лет:
3. Удельный вес живорожденных, родившихся у женщин в возрасте 25-29 лет:
4. Удельный вес живорожденных, родившихся у женщин в возрасте 30-34 лет:
5. Удельный вес живорожденных, родившихся у женщин в возрасте 35-39 лет:
6. Удельный вес живорожденных, родившихся у женщин в возрасте 40-44 лет:
7. Удельный вес живорожденных, родившихся у женщин в возрасте 45-49 лет:
III. Сводная таблица относительных величин.
IV. Графическое изображение интенсивного показателя. Столбиковая диаграмма
Рис.1.Повозрастная плодовитость женщин детородного возраста.
V. Графическое изображение экстенсивного показателя. Внутристолбиковая диаграмма
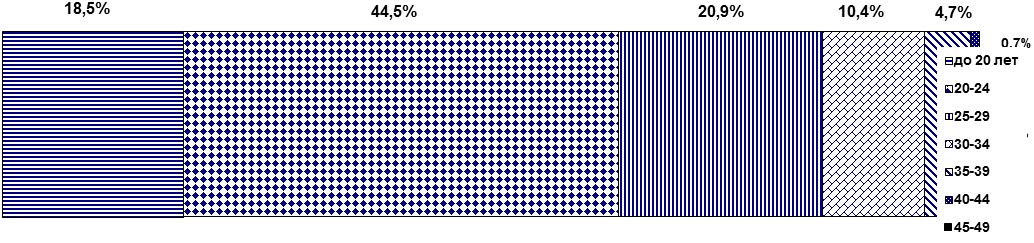
Рис.2. Распределение живорожденных по возрасту матери. Секторная диаграмма
Рис. 3. Распределение живорожденных по возрасту матери. ВЫВОД: Анализ интенсивных показателей повозрастной плодовитости женщин детородного возраста города М. показывает, что самый высокий уровень плодовитости приходится на возрастную группу от 20 до 24 лет – 161,2‰, что в 3,5 раз выше показателя общей плодовитости (46,5‰). Самый низкий уровень плодовитости приходится на возрастные группы от 40 до 44 лет – 2,4‰ и от 45 до 49 лет – 1,2‰, что во много раз ниже показателя общей плодовитости женщин (46,5%). Оценивая экстенсивные показатели, можно сделать вывод, что наибольший удельный вес живорождений среди всех женщин детородного возраста приходится на возрастную группу от 20 до 24 лет – 44,5%. А наименьшая доля живорожденных приходится на возрастные группы от 40 до 44 лет – 0,7% и от 45 до 49 лет – 0,2%.
ТАБЛИЦЫ: 1. Виды относительных величин. 2. Графические изображения относительных величин.
МЕТОДИЧЕСКАЯ РАЗРАБОТКА ПРАКТИЧЕСКОГО ЗАНЯТИЯ ДЛЯ СТУДЕНТОВ, ОБУЧАЮЩИХСЯ НА СПЕЦИАЛЬНОСТИ «ЛЕЧЕБНОЕ ДЕЛО» ПО ТЕМЕ: ”СРЕДНИЕ ВЕЛИЧИНЫ. МЕТОДИКА ВЫЧИСЛЕНИЯ И ОЦЕНКА ДОСТОВЕРНОСТИ. ПРАКТИЧЕСКОЕ ИСПОЛЬЗОВАНИЕ В МЕДИЦИНЕ”
ЦЕЛЬ ЗАНЯТИЯ: овладеть методикой составления вариационных рядов и вычисления средних величин при малом (n£30) и большом (n>30) числе наблюдений; овладеть методикой расчета ошибки и доверительных границ средних величин; научиться оценивать достоверность результатов исследования. МЕТОДИКА ПРОВЕДЕНИЯ ЗАНЯТИЯ: 1. определение исходного уровня знаний студентов; 2. разъяснение наиболее сложных для восприятия вопросов. 3. самостоятельная работа студентов: изучение типовых заданий, выполнение заданий. ОСНОВНЫЕ ВОПРОСЫ ТЕМЫ:
В медицине, в здравоохранении очень часто используются выражаемые числами признаки, которые могут принимать различные числовые значения у разных единиц совокупности, нередко повторяющиеся у нескольких единиц. Например, пульс, АД, температура тела, длительность временной нетрудоспособности, длительность пребывания в стационаре отличаются (варьируют) у больных даже с одним диагнозом. Полученные при исследовании величины сначала записываются хаотично, т.е. в том порядке, как их получает исследователь. Ряд, в котором упорядоченно сопоставлены (по степени возрастания или убывания) варианты и соответствующие им частоты, называется вариационным. Отдельные числовые значения признака называются вариантами (V), а числа, показывающие, как часто эти варианты повторяются - частотами (Р), общее число наблюдений (n) равно сумме частот (n=SP, S - знак суммы). Вариационный ряд может быть простым или сгруппированным. Простой вариационный ряд составляется при малом числе наблюдений (n£30), а сгруппированный - при большом числе наблюдений (n>30). Построение вариационного ряда из отдельных вариант – это только первый шаг к осмыслению особенностей всей совокупности. Далее для обобщенной числовой характеристики изучаемого признака у совокупности обследуемых рассчитываются средние величины, достоинство которых заключаются в том, что одна величина характеризует большую совокупность однородных явлений. Средняя величина – это число, выражающее общую меру исследуемого признака в совокупности. Различают несколько видов средних величин: мода (Мо), медиана (Ме) и средняя арифметическая (М). Мода (Мо) - наиболее часто повторяющаяся варианта, т.е. та, которой соответствует наибольшее количество частот (Р) вариационного ряда. Медиана (Ме) - варианта, занимающая срединное положение в вариационном ряду. При нечетном числе наблюдений для определения медианы надо найти середину ряда – медианой будет центральная (срединная) варианта. При четном числе наблюдений за медиану принимают среднюю величину из двух центральных вариант. Наиболее часто используется средняя арифметическая величина. Средняя арифметическая имеет 3 основных свойства: 1. Занимает срединное положение в вариационном ряду. В строго симметричном ряду М = Мо = Ме; 2. Имеет абстрактный характер и является обобщающей величиной, вскрывающей то типичное, что характерно для всей совокупности. 3. Алгебраическая сумма отклонений всех вариант от средней равна нулю. Если сумма отклонений вариант от средней равна нулю, то средняя вычислена правильно. На этом свойстве основан расчет средней по способу моментов. Основными способами расчета М являются: 1) среднеарифметический способ – применяется для вычисления средней арифметической простой и средней арифметической взвешенной; 2) способ моментов (условных отклонений) – используется в случаях, когда варианты состоят из многозначных чисел, а совокупность – из большого числа наблюдений. Средняя арифметическая, которая рассчитана в вариационном ряду, где каждая варианта встречается только один раз (для всех вариант р=1), называется средней арифметической простой. Она определяется по формуле:
где М – средняя арифметическая, V – значение вариационного признака, n – общее число наблюдений
Если в исследуемом ряду отдельные варианты встречаются различное число раз (р³1), то вычисляют среднюю арифметическую взвешенную. Расчет ее производится по формуле:
При большом количестве наблюдений (n>30) число размеров вариант может быть очень большим, тогда рекомендуется размеры вариант объединять в группы. При составлении сгруппированного вариационного ряда необходимо: 1. определить количество групп в ряду; 2. определить интервал между группами по формуле: 3. определить середину интервала – полусумма первых значений соседних групп; 4. распределить изучаемую совокупность по группам; 5. составить графическое изображение вариационного ряда.
Пример определения средней арифметической в сгруппированном вариационном ряду представлен ниже. ТИПОВОЕ ЗАДАНИЕ
На основе приведенных в таблице данных: 1. определите моду (Мо) и медиану (Ме); 2. вычислите взвешенную среднюю арифметическую (М), среднее квадратическое отклонение (d), коэффициент вариации (Сv), ошибку репрезентативности (m) и определите доверительные границы средней с вероятностью безошибочного прогноза P=95,5% и при P=99,7%; 3. используя полученные результаты, сделайте соответствующие выводы.
При взвешивании мальчиков 9 лет получены следующие данные:
Образец выполнения задания
Средняя арифметическая (M)
Мо = 25 кг Ме = 25 кг
Это абстрактная величина, за ней не видны колебания веса мальчиков в ряду, сумма отклонения всех вариант от средней арифметической = 0. В строго симметричном ряду она занимает срединное положение, в нашем случае средняя арифметическая совпадает с модой и медианой, значит ряд строго симметричный.
2. Среднее квадратическое отклонение (d)
Средний вес мальчиков с учетом сигмальных отклонений
86 – 100% 83 – X
В нормальном ряду распределения в пределах М±2d должно быть не менее 95,5% вариант вариационного ряда. В нашем случае 96,5% мальчиков находятся в этих пределах. Только 3 мальчика имеют вес ниже 21,1 кг и ни одного нет с весом больше 29,1 кг. Следовательно, средний вес мальчиков 25,1 кг является типичным, и ряд соответствует ряду с нормальным распределением признака.
3. Коэффициент вариации (Cv)
Cv является относительной мерой разнообразия. Полученный коэффициент вариации (Сv) меньше 10%, следовательно, можно считать, что степень колеблемости веса мальчиков 9-летнего возраста слабая.
МЕТОДИЧЕСКАЯ РАЗРАБОТКА ПРАКТИЧЕСКОГО ЗАНЯТИЯ ДЛЯ СТУДЕНТОВ, ОБУЧАЮЩИХСЯ Анализ динамического ряда
Чтобы проанализировать динамический ряд нужно изобразить его графически и вычислить ряд показателей:
· Абсолютный прирост (убыль) – разность между последующим и предыдущим уровнем. Измеряется в тех же единицах, в которых представлены уровни ряда.
· Показатель роста (убыли) – отношение каждого последующего уровня к предыдущему, принятому за 100%. Он показывает сколько % от предыдущего уровня составляет последующий уровень.
· Темп прироста (убыли) – отношение абсолютного прироста (убыли) каждого последующего уровня к предыдущему уровню, принятому за 100%. Он показывает на сколько % увеличился (снизился) последующий уровень по сравнению с предыдущим и поэтому может быть рассчитан по формуле: темп прироста = темп роста – 100% · Показатель наглядности – отношение каждого уровня ряда к одному из них (чаще начальному) принятому за 100%.
Рассчитанные показатели будут свидетельствовать о тенденциях изучаемого явления в динамике. ТИПОВОЕ ЗАДАНИЕ
На основе приведенных данных: I. Вычислить и представить в виде таблицы показатели динамического ряда: 1) абсолютный прирост (убыль); 2) показатель роста (убыли); 3) темп прироста (убыли); 4) показатель наглядности. II. Изобразить показатели наглядности графически. III. Проанализировать динамический ряд и сделать выводы.
Динамика смертности в РФ за ряд лет:
ОБРАЗЕЦ ВЫПОЛНЕНИЯ ЗАДАНИЯ Динамика смертности в РФ
МЕТОДИЧЕСКАЯ РАЗРАБОТКА ПРАКТИЧЕСКОГО ЗАНЯТИЯ ДЛЯ СТУДЕНТОВ, ОБУЧАЮЩИХСЯ ТИПОВОЕ ЗАДАНИЕ На основе приведенных данных: 1. Определить коэффициент корреляции (rxy) и по его величине оценить силу связи между изучаемыми явлениями и ее направленность. 2. Оценить степень достоверности полученного коэффициента корреляции, определив его среднюю ошибку (mr). 3. Сделать соответствующие выводы.
Исследования крови у 9-ти здоровых мужчин показали следующее содержание гемоглобина и легко отщепляемого железа:
ОБРАЗЕЦ ВЫПОЛНЕНИЯ ЗАДАНИЯ Корреляция между содержанием легко отщепляемого железа И гемоглобина в крови
Коэффициент корреляции (rxy)
Средняя ошибка коэффициента корреляции (mr).
Степень вероятности безошибочного прогноза (по Н.А.Плохинскому) P>99%, но меньше 99,9%, так как при n'= n–2 = 9–2 = 7, полученный нами критерий t=4,9 будет больше tтабл. = 3,5, которому соответствует Р = 99%, но меньше tтабл. = 5,3, которому соответствует Р = 99,9%.
ВЫВОДЫ:
Коэффициент корреляции rxy, равный 0,88 означает, что между величиной легко отщепляемого железа и содержанием гемоглобина в крови существует прямая сильная связь, т.е. чем больше легко отщепляемого железа, тем выше содержание гемоглобина в крови. Полученный в данном выборочном исследовании результат достоверен, поскольку коэффициент корреляции превышает величину трех своих ошибок (0,88>3´0,18), и доверительный критерий t составляет 4,9. Следовательно, с вероятностью безошибочного прогноза Р>99%, можно утверждать, что и в генеральной совокупности существует сильная прямая связь между количеством легко отщепляемого железа и содержанием гемоглобина в крови.
ТАБЛИЦЫ: 1. Пример вычисления коэффициента ранговой корреляции и его ошибки. 2. Пример вычисления коэффициента корреляции Пирсона и его ошибки.
МЕТОДИЧЕСКАЯ РАЗРАБОТКА ПРАКТИЧЕСКОГО ЗАНЯТИЯ ДЛЯ СТУДЕНТОВ, ОБУЧАЮЩИХСЯ ТИПОВОЕ ЗАДАНИЕ Женщины детородного возраста по возрасту и числу родившихся у них детей распределились в двух районах следующим образом:
Вычислить стандартизованные показатели плодовитости в городах “А” и “Б” по прямому методу и, сравнив их с интенсивными показателями плодовитости, вычисленными обычным путем, сделать соответствующие выводы. ОБРАЗЕЦ ВЫПОЛНЕНИЯ ЗАДАНИЯ
I ЭТАП – вычисление “повозрастных” и общих интенсивных коэффициентов плодовитости женщин в городах “А” и “Б”.
II ЭТАП – выбор и расчет стандарта. В нашем примере за стандарт принята суммарная численность женщин 2-х городов.
III ЭТАП – расчет “ожидаемых чисел” живорожденных в каждой группе стандарта. Мы определяем, сколько было бы живорождений в каждой возрастной группе женщин городов “А” и “Б” при имеющихся повозрастных интенсивных показателях плодовитости, но при новом возрастном составе, принятом за стандарт. Например, в возрастной группе женщин 15-20 лет в городе “А” число живорождений составило бы:
А в городе “Б” “ожидаемое число” живорожденных у женщин в возрасте 15-20 лет составит:
IV ЭТАП – расчет стандартизованных показателей общей плодовитости женщин в городах “А” и “Б”. Просуммировав абсолютные “ожидаемые числа” живорожденных по каждому городу отдельно, полученные суммы соотносим с суммарной численностью женщин двух городов, принятой за стандарт. Так, в городе “А” стандартизованный показатель плодовитости женщин составит:
А в городе “Б” стандартизованный показатель плодовитости женщин составит: Таблица 1 МЕТОДИЧЕСКАЯ РАЗРАБОТКА ПРАКТИЧЕСКОГО ЗАНЯТИЯ ДЛЯ СТУДЕНТОВ, ОБУЧАЮЩИХСЯ НА СПЕЦИАЛЬНОСТИ «ЛЕЧЕБНОЕ ДЕЛО» ПО ТЕМЕ: «СТАТИСТИЧЕСКАЯ СОВОКУПНОСТЬ.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 866; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.118.151 (0.01 с.) |


 ‰
‰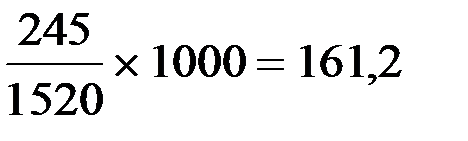 ‰
‰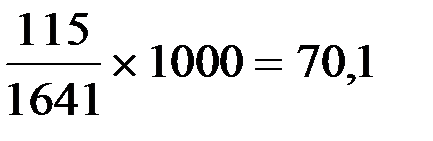 ‰
‰ ‰
‰ ‰
‰ ‰
‰ ‰
‰ ‰
‰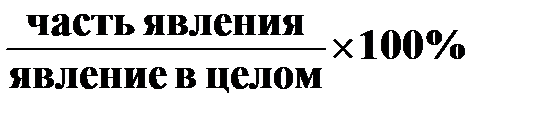
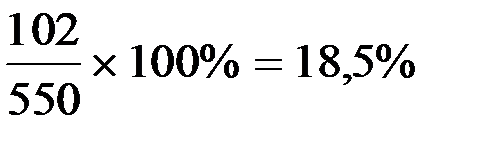




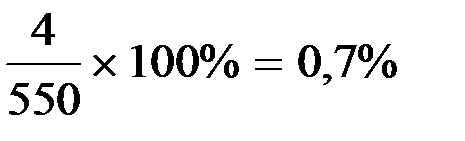




 где Р – частота, n – сумма частот (å P).
где Р – частота, n – сумма частот (å P). ;
; »25кг
»25кг кг
кг

 =69
=69
 =52
=52


 = ±0,18
= ±0,18 
 = 264
= 264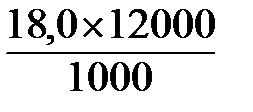 = 216
= 216 ´ 1000 = 76,2 ‰.
´ 1000 = 76,2 ‰. ´ 1000 = 67,3 ‰.
´ 1000 = 67,3 ‰.


