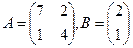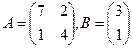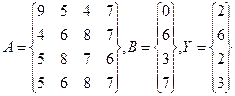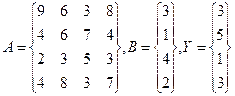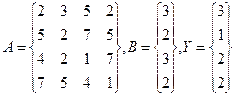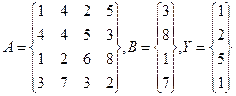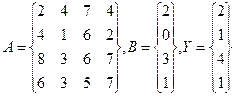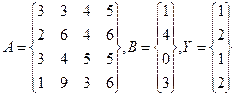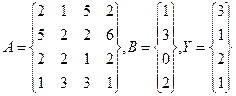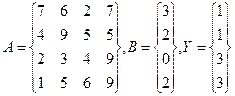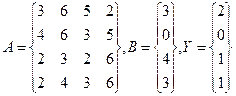Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нахождение суммы числового рядаСодержание книги Поиск на нашем сайте
Цель работы
Найти сумму числового ряда и сравнить ее с точным решением (таблица 2).
Пояснение к задаче Аналогично лабораторной работе 2 получаем первый столбец значений К, где 1<=K<=N, и столбец f(K). Далее выделяем столбец f(K) и нажимаем на кнопку “автосумма” Строки инструментов. Полученное значение суммы запишется под столбцом f(K). Можно получить значение суммы, например, по формуле: = СУММ(С5:С14), где С5:С14- диапазон ячеек столбца f(K), а ячейка С15 содержит формулу суммы.
Варианты заданий
Лабораторная работа №5 Работа с массивами 1. Цель работы: Цель работы – научиться производить расчеты по формулам, зависящим от большого массива данных. Примеры решения задач Пример 1 В качестве первого примера простой операции над массивами рассмотрим умножение массива А1:B2 на число 5, Выделите на рабочем листе область, например, D1:E2, такого же размера, как и массив – множимое (рис. 9),
Рис. 9. Выделение диапазона для ввода результирующего массива Теперь введите формулу =A1:B2*5, Для этого установите курсор в строке формул и закончите ввод не как обычно нажатием клавиши Enter, а нажатием клавиш Ctrl + Shift + Enter, Таким образом, вы сообщите программе, что необходимо выполнить операцию над массивом, При этом Excel заключит формулу в строке формул в фигурные скобки (рис. 10): { = А1:В2*5 }
Рис. 10. Произведение массива на число При работе с массивами формула действует на все ячейки диапазона, Нельзя изменять отдельные ячейки в операндах формулы, Аналогично можно вычислить сумму (разность) массивов (рис. 11).
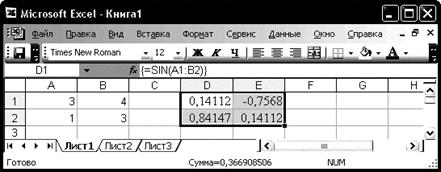
Рис. 11. Сумма двух массивов Аналогично можно определить массив, каждый элемент которого связан посредством некоторой функции с соответствующим элементом первоначального массива (рис. 12)
Рис. 12. Вычисление функции от каждого элемента массива.
В Excel имеются специальные встроенные функции для работы с матрицами: МОБР (MINVERSE) Обратная матрица МОПРЕД (MDETERM) Определитель матрицы МУМНОЖ (MMULT) Матричное произведение двух матриц ТРАНСП (TRANSPOSE) Транспонированная матрица Во всех случаях при работе с матрицами перед вводом формулы надо выделить область на рабочем листе, куда будет выведен результат вычислений, Решим в качестве примера систему линейных уравнений с двумя неизвестными, матрица коэффициентов которой записана в ячейки F1:G2, а свободные члены – в ячейки I1:I2 (рис. 13), Для решения этой задачи вспомним, что решение линейной системы АХ = В, где А – матрица коэффициентов, В – столбец (вектор) свободных членов, Х – столбец (вектор) неизвестных, имеет вид Х = А–1В, где А–1 – матрица, обратная по отношению к А, Поэтому для решения нашей системы уравнений выделим под вектор решений диапазон К1:К2 и введем в него формулу, как показано на рис. 13.
Рис. 13. Решение системы линейных уравнений. Решим также систему линейных уравнений А2Х = В, где
Для решения этой системы введем в диапазон ячеек А1:В2 элементы матрицы А, а в диапазон ячейки D1:D2 – элементы столбца свободных членов В, Выберем диапазон Fl:F2, куда поместим элементы вектора решения, и введем следующую формулу: { = МУМНОЖ(МОБР(МУМНОЖ(А1:В2;А1:B2));D1:D2) } Рассмотрим пример вычисления квадратичной формулы z = XT АХ, где А – квадратная матрица, введенная в диапазон А1:В2, X – вектор, введенный в диапазон D1:D2, а символ (Т) обозначает операцию транспонирования, Для вычисления z введем в ячейку F1 (рис. 14) формулу: { = МУМНОЖ(МУМНОЖ(ТРАНСП(D1:D2);A1:B2);D1:D2) }
Рис. 14. Нахождение квадратичной формы. Хотя результатом этой формулы является число, не забудьте для ее ввода нажать клавиши Ctrl + Shift + Enter, Если этого не сделать, в ячейке F1 появится сообщение #ЗНАЧ! Вычислим теперь значение квадратичной формы z = YT АT АY, где
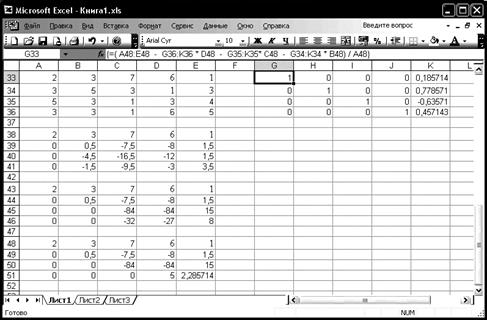
Для решения этой задачи введем в диапазон ячеек А1:В2 элементы матрицы А, а в диапазон D1:D2 – элементы столбца Y, Для вычисления квадратичной формы введем в ячейку F1 формулу: { = МУМНОЖ(ТРАНСП(D1:D2);МУМНОЖ(ТРАНСП(A1:B2);МУМН0Ж(A1:B2;D1:D2))) } Пример 2 В качестве следующего примера работы с массивами рассмотрим решение системы линейных уравнений методом Гаусса, На рис. 15 приведены результаты решения методом Гаусса следующей системы линейных уравнений:
2х1 + 3x2 + 7х3 + 6х4 = 1, Зх1, + 5x2 + Зх3 + x4 = 3, 5x1 + 3x2 + x3 + 3x4 = 4, Зх1 + 3х2 + х3 + 6х4 = 5
Рис. 15. Пошаговое решение системы линейных уравнений методом Гаусса. E33:E36 введены матрица коэффициентов и столбец свободных членов, соответственно, Содержимое ячеек A33:E33 скопировано в ячейки A38:E38, А43:E43 и A48:E48, В диапазон ячеек А39:Е39 введена формула: { = A34:E34 – $A$33:$E$33*(A34/$A$33) }, обращающая в нуль коэффициент при xt во втором уравнении системы. Выделим диапазон А39:A39 и протащим маркер выполнения этого диапазона так, чтобы выполнить диапазон А39:E41, Это обратит в нуль коэффициент при х1 в третьем и четвертом уравнениях системы, Скопируем значения из диапазона ячеек А39:Е39 в диапазоны A44:E44 и А49:E49, Для копирования значений без формул воспользуйтесь командой Правка, Специальная вставка (Edit, Special Paste) и в открывшемся диалоговом окне Специальная вставка (Special Paste) в группе Вставить (Paste) установите переключатель в положение Значение (Value) (рис. 16),
Рис. 16. Меню: “Специальная вставка”. В диапазон ячеек А45:Е45 вводим формулу: { = A40:E40 – A$39:$E$39*(B40/$B$39) }, Выделим диапазон A45:E45 и протащим маркер заполнения этого диапазона так, чтобы заполнить диапазон A45:E46, Это обратит в нуль коэффициент при x2 в третьем и четвертом уравнениях системы, Копируем значения из диапазона ячеек А45:Е45 в диапазон A50:E50, В диапазон ячеек A51:E51 вводим формулу { = A46:E46 – $A$45:$E$45*(С46/$С$45) }, которая обращает в нуль коэффициент при х3 четвертого уравнения системы, Прямая прогонка метода Гаусса завершена, Обратная прогонка заключается в вводе в диапазоны G36:K36, G35:K35,G34:K34 и G33:K33, соответственно, следующих формул: { = A51:E51/D51) { = (A50: E50 – G36: K36 * D50) / С50 } { = (A49:E49 – G36: K36* D49 – G35: K35 * С49) / B49 } { = (A48: E48 – G36: K36 * D48 – G35: K35* С48 – G34: K34 * B48) / A48 } В диапазоне ячеек K33:К36 получено решение системы. Варианты заданий
ЛАБОРАТОРНАЯ РАБОТА № 6
|
||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 461; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.243.41 (0.01 с.) |

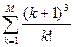 ; M=10
; M=10
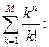 n=4, M=12
n=4, M=12
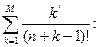 n=5, M=8
n=5, M=8
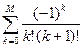 ; M=10
; M=10
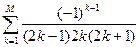 ; M=1
; M=1
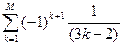 ; M=10
; M=10
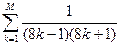 ; M=12
; M=12
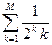 ; M=1
; M=1
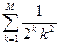 ; M=8
; M=8
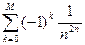 : n=3, M=10
: n=3, M=10
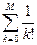 ; M=8
; M=8
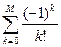 ; M=10
; M=10
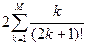 ; M=8
; M=8
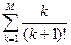 ; M=10
; M=10
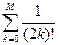 ; M=8
; M=8
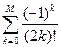 ; M=8
; M=8
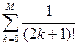 ; M=10
; M=10
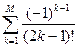 ; M=8
; M=8
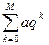 : a=2,7:
q=0,5, M=12
: a=2,7:
q=0,5, M=12
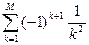 ; M=14
; M=14
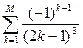 ; M=14
; M=14
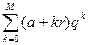 ;
a=3,7; r=1,1; q=-0,5, M=12
;
a=3,7; r=1,1; q=-0,5, M=12
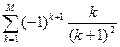 ; M=15
; M=15
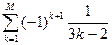 ; M=16
; M=16
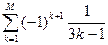 ; M=14
; M=14
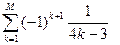 ; M=16
; M=16
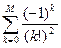 ; M=8
; M=8
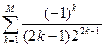 ; M=8
; M=8
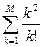 ; M=10
; M=10
 15e
15e
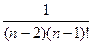 0,476725
0,476725
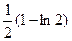
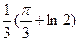
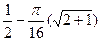 ln(2)
ln(2)
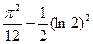 n2/(n2+1)
e
n2/(n2+1)
e
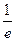
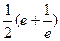 cos1
cos1
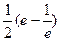 sin1
sin1
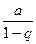
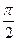
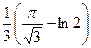
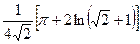 0,223891
0,576725
arctg2-
0,223891
0,576725
arctg2-