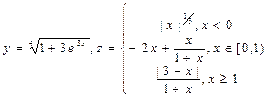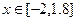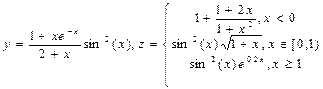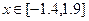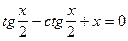Операции, производимые с документом в целом

Минимальный набор типовых операций включает операции, производимые над документом в целом, над абзацами документа и над его фрагментами. К операциям, производимым с документом, относятся:

• создание нового документа — присвоение документу уникального имени и набор всего текста документа на клавиатуре;

• загрузка предварительно созданного документа в оперативную память;

• сохранение документа —- копирование документа из оперативной памяти во внеш­нюю;

• удаление документа — удаление созданного или загруженного документа с экрана;

• распечатка документа — создание твердой (бумажной) копии документа.

Операции, производимые над абзацами документа

Абзац является ключевым элементом в структуре документа для многих текстовых процес­соров (хотя имеются и другие, например, разделы).

Указанные операции включают установку границ абзацев и абзацных отступов, вырав­нивание, а также включение переноса слов.

Установку границ абзацев производят с помощью маркеров отступов, находящихся на координатной линейке, или соответствующими командами меню.

Выравнивание (выключка). Различают четыре вида горизонтального (влево, вправо, по центру, по ширине) и три вида вертикального выравнивания (вверх, вниз, по высоте).

Перенос. При выключенном режиме автоматического переноса слово, не поместив­шееся на строке, полностью переносится на следующую строку. Это не придает элегантности тексту; его правый край остается неровным. Для улучшения внешнего вида текста ис­пользуют режим переноса. При ручном варианте переноса пользователь сам определяет место переноса, вводя дефис, и жестким переводом каретки (нажатием на клавишу <Enter>) переходит на следующую строку. Использование такого режима переноса приводит к необ­ходимости удаления дефисов при повторном форматировании текста документа.

При включенном режиме автоматического переноса реализуется мягкий вариант пере­носа: текстовый процессор сам делит слово на слоги и переносит его наилучшим способом. Этот режим не создает никаких трудностей при повторном форматировании.

Операции, производимые с фрагментами текста

Эти операции включают выделение фрагмента текста, его перемещение, копирование или удаление, которые были рассмотрены в предшествующем разделе главы. Кроме того, выде­ленный фрагмент текста можно напечатать, произвести поиск и замену символов, приме­нить шрифтовое выделение и ряд других операций.

 

Цель работы

Изучение технологии ввода и редактирования текстовых документов. Создание формул, таблиц, графиков в среде MS WORD. Освоение расширенных возможностей редактора MS WORD.

 

Порядок выполнения работы

 

3.1 Введите несколько абзацев на русском языке, поясняющих цель и задания вашей лабораторной работы и один на английском языке, используя различные шрифты, размеры букв. Примените к набранному тексту различные виды форматирования.

3.2 Проверьте орфографию на обоих языках.

3.3 Сохраните документ в файле. Установите режим автосохранения через каждые 5 минут.

3.4 Вставьте в текст блок-схему алгоритма, выполненную с помощью встроенного графического редактора. Покажите на схеме различные способы вставки пояснений.

3.5 Создайте по таблице (Приложение 1) 2-хмерные и 3-хмерные диаграммы с заголовками, метками и легендой (редактор диаграмм MS GRAPH).

3.6 Введите формулы с помощью редактора формул MS EQUATION (Приложение 2).

3.7 С помощью Мастера Таблиц создайте таблицу со следующими графами: Марка компьютера или внешнего устройства; цена; количество товара. Добавьте столбец с суммарной стоимостью. С помощью опции Автоформат выберите внешний вид таблицы.

Скопируйте таблицу и поработайте с редактором таблиц: добавить – удалить строки; разделить таблицу на части; преобразовать таблицу в текст и обратно; измените ширину столбцов и строк.

3.8 Создайте верхний и нижний колонтитул. В верхнем укажите дату и время создания работы, в нижнем – номер лабораторной работы, группу и ФИО.

3.9 На первом листе работы вставьте в качестве эмблемы готовое изображение из библиотеки ClipArt. Рядом с эмблемой вставьте «УГАТУ – ПИЭ» с помощью редактора WordArt. Используйте различные свойства объекта: гарнитуру, размер шрифта, закраску, тени, способ расположения текста.

3.10 Создайте нумерованный и ненумерованный список. Создайте многоуровневый список.

3.11 Для пояснений к таблице с ценами компьютеров поставьте сноски.

3.12 В начале работы наберите текст с пояснениями к диаграммам или формулам и установите перекрестную ссылку на соответствующую иллюстрацию.

3.13 Проведите контекстный поиск и замену.

3.14 Установите режим просмотра текста перед печатью и откорректируйте окончательный вид документа.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Назначение текстовых процессоров. Виды текстовых процессоров.

2. Вызов справки. Поиск по справке.

3. Работа с абзацами.

4. Проверка орфографии.

5. Выделение фрагмента текста. Работа с фрагментом.

6. Режим «Рисование».

7. Ввод формул.

8. Сноски и ссылки.

9. Сохранение файла.

10. Просмотр файла перед печатью

ПРИЛОЖЕНИЕ 1

 

Компоненты	Объемная доля, %	Массовая доля, %	Молекулярная масса
N2	78.09	75.5
O2	20.95	23.1
Ar	0.93	1.3
CO2	0.03	0.05
Всего

Рисунок 2

 

ПРИЛОЖЕНИЕ 2

 

 

 

 

Рисунок 3

Лабораторная работа № 2

Построение графиков

Введение

Excel относится к программным продуктам, которые известны под на­званием электронные таблицы. При запуске Excel в окне документа появля­ется пустая рабочая книга. Рабочая книга - это основной документ, исполь­зуемый Excel для хранения и обработки данных. Рабочая книга состоит из отдельных рабочих листов, каждый из которых может содержать данные. По умолчанию каждая вновь созданная рабочая книга содержит 3 рабочих листа, но их количество можно изменять. Кроме рабочих листов, можно соз­давать диаграммы, макросы и листы диалога.

Каждый рабочий лист состоит из 256 столбцов и 65536 строк. Столбцы обозначены буквами, начиная от А до Z, далее - от АА до AZ, затем - от ВА до BZ и так далее до столбца IV. Эти обозначения отображаются вверху окна документа. Строки пронумерованы вниз от 1 до 65536 с левой стороны окна документа.

Пересечения строк и столбцов формируют ячейки, являющиеся основ­ной единицей хранения данных. Каждая ячейка имеет свое - обозначение, в котором указывается соответствующий столбец и строка и которое использу­ется как адрес ячейки или, иначе говоря, как ссылка на ячейку. Например, С5 - адрес ячейки на пересечении столбца С и строки 5.

Ссылки могут быть абсолютными, относительными и смешанными. Абсолютная часть ссылки помечается символом $. Например, $А1, А$1, $А$1. Относительная часть ссылки не помечается. Основная причина использования разных типов ссылок - их поведение при копировании ячеек. Относи тельные ссылки (или относительные части ссылок) при копировании изменяются, абсолютные ссылки не изменяются. Например, в ячейке А2 находится формула =А1+$В$2. При копировании ячейки А2 в ячейку СЗ формула в СЗ будет иметь вид = С2+$В$2.

Ячейки электронных таблиц могут содержать числа в различных фор матах, строки и формулы. В формулах используются знаки операций, круглые скобки и операнды. Операндами могут быть числа, встроенные функции и ссылки на ячейки или диапазоны. Если ссылка указывает на ячейку, содержащую значение, вычисления проводятся с этим значением. Если ссылка указывает на ячейку, содержащую формулу, в расчетах используется результат вычислений по формуле. Если ссылка указывает на пустую ячейку, она не учитывается при расчетах.

Электронные таблицы содержат большие наборы встроенных функций.

Цель работы

Цель работы - научиться с помощью мастера диаграмм строить графики для более наглядного представления данных.

Примеры решения задач

Пример 1

Рассмотрим процедуру построения графика функции

Y - cos² (px) при х Î [0,1 ].

Для построения графика функции, необходимо сначала построить таб­лицу ее значений при различных значениях аргумента, причем аргумент изменяется с фиксированным шагом. Будем считать, что шаг h = 0,1. Необходимо найти y(0), y(0,1), у(0,2),..., у(1). С этой целью в диапазон ячеек А1:А11 надо ввести значения переменной х0, 0,1, 0,2 0,3... 1. Отметим, что выбранные значения переменной образуют арифметическую прогрессию. Заполнение ячеек членами арифметической прогрессии в Excel можно осуще­ствить двумя способами.

Первый способ. В ячейки А1 и А2 введите первый и второй члены арифметической прогрессии и выделите эти ячейки. После этого установите указатель мыши на маркере заполнения выделенного диапазона (рис. 1) и протащите его вниз до тех пор, пока не получится числовой ряд.

Рис. 1. Указатель мыши на маркере заполнения

Второй способ. В ячейку А1 введите первый член арифметической прогрессии. Выберите команду Правка, Заполнять, Прогрессия (Edit, Fill, Series) и в открывшемся диалоговом окне Прогрессия (Series) (рис. 2) в группе Расположение установите переключатель в положение По столбцам, а в группе Тип - в положение Арифметическая. В поля Шаг и Предельные значения введите нужные значения.

 

Рис. 2. Диалоговое окно Прогрессия

Затем в ячейку В1 введите формулу =COS(ПИ()*А1)^2.

Ввод формул в ячейку можно производить с клавиатуры или с помощью диалогового окна Мастер функций, вызываемого командой Вставка, Функци я (Insert, Function) или нажатием кнопки ƒ- панели инструментов Стандартная (Standart). Мастер функций содержит список всех встроенных в Excel функций, а также справки по синтаксису функций и примеры их применения. Отметим, что при использовании мастера функции перед вводом формулы в ячейку не надо вводить знак "=", так как мастер функций введет его сам.

Для того чтобы завершить процесс табулирования функции, выделите ячейку В1, установите указатель мыши на маркере заполнения и протащите его вниз до ячейки В11.

Для построения графика функций вызовите мастер диаграмм с помо­щью команды Вставки, Диаграмма (Insert, Chart) или нажатием кнопки на панели инструментов Стандартная (Standard).

На первом шаге мастера диаграмм выберите тип диаграммы - Графи к и вид графика.

На фтором шаге введите диапазон ячеек В1:В11, по которому будет строиться график и установите переключатель Ряды в положение В столбцах.

 

Рис. 3. Диалоговое окно Исходные данные

 

Выберите вкладку Ряд (рис. 3) и в открывшемся диалоговом окне Источник

данных диаграммы в поле Подписи по оси X введите диапазон А1:А11.

На третьем шаге мастера диаграмм в окне Параметры диаграммы, выбирая нужные вкладки, введите название диаграммы, подписи по оси X и Y, добавьте легенду и т.д. (рис. 4).

 

Рис. 4. Параметры диаграммы

На четвертом шаге мастера диаграмм укажите, где будет размещен график: на отдельном листе или на имеющемся.

Нажмите кнопку Готово, график построен (рис. 5).

Рис. 5. Результат построения графика функции

Пример 2

Рассмотрим пример построения графика функции

x Î [0,1].

Этот график строится также, как и в примере 1, за одним исключением в ячейку В1 вводится формула:

ЕСЛИ(А1 < 0,5; 1 – ABS (0,2-A1)) / (1+A1+A1^2);A1^(1/3))

Варианты заданий

Таблица 1. Построить в разных системах координат графики следующих функций:

 

Лабораторная работа № 3

Нахождение корней уравнения

Цель работы

Цель работы - научиться находить определенный результат для ячейки С с помощью подбора значения другой ячейки на примере полиномов различ­ных степеней.

Примеры решения задачи

Рассмотрим пример нахождения всей корней уравнения

х³ + 0.01x² - 0,7044х + 0,139104= 0.

Отметим, что у полиномов третей степени имеется не более трех вещественных корней. Для нахождения корней их предварительно нужно локализовать. Для этого постройте график функции или протабулируйте ее. Например, протабулируем наш полином на отрезке [-1, 1] с шагом 0,2. Результат табулирования приведен на рис. 6, где в ячейку В2 введена следующая формула:

= А2 ^ З - 0,01 * A2 ^ 2 - 0,7044 * A2 + 0, 139104.

Рис. 6. Локализация корней полинома

Из рис. 6 видно, что полином меняет знак на интервалах: [-1; -0,8], [0,2; 0,4] и [0,6; 0,8]. Это означает, что на каждом из них имеется корень данного полинома.

Найдем корни полинома методом последовательных приближений с помощью команды Сервис, Подбор параметра (Tools, Goal Seek). Относи тельная погрешность вычислений и предельное число итераций задаются на вкладке Вычисления диалогового окна Параметры, открываемого командой Сервис, Параметры

Задайте относительную погрешность и предельное число итераций, равным 0.00001 и 1000, соответственно.

В качестве начальных значений приближений к корням выберите любые точки из отрезков локализации корней. Например, их средние точки: -0,9, 03 и 0,7. Введите их в диапазон ячеек С2:С4. В ячейку D2 введите фор мулу

=С2 ^ 3 - 0,01 * С2 ^ 2 - 0,7044 * С2 + 0,139104.

Выделите эту ячейку и с помощью маркера заполнения протащите введенную в нее формулу на диапазон D2:D4. Таким образом, в данном диапазоне будет вычисляться значения полинома для всех начальных значений.

Выберите команду Сервис, Подбор параметра и заполните диалого­вое окно Подбора параметра (рис. 7).

Рис. 7. Диалоговое окно «Подбор параметра»

В поле Установить в ячейке введите D2. В этом поле дается ссылка на ячейку, в которую введена формула, вычисляющая значение левой части уравнения. В поле Значение введите 0 (в этом поле указывается правая часть уравнения). В поле Изменяя значения ячейки введите С2 (в этом поле дается ссылка на ячейку, отведенную под переменную).

Вводить ссылки на ячейки удобнее не с клавиатуры, а щелчком на соответствующей ячейке. При этом Excel автоматически будет превращать их в абсолютные ссылки.

После нажатия кнопки ОК средство подбора параметров находит приближенное значение корня, которое помешает вячейку С2. Для рассмотрен­ного примера оно равно -0,92034. Вид диалогового окна Результат подбора параметра после успешного завершения поиска решения показан на рис 8.

Рис. 8. Диалоговое окно «Результат подбора параметра»

Аналогично в ячейках СЗ и С4 найдите два оставшихся корня

 

 

Варианты заданий

Найти все корни уравнения Таблица 2

№
	x^3 – 2,92x^2 + 1,4355x + 0,791136 = 0
	x^3 – 2,56x^2 – 1,3251x + 4,395006 = 0
	x^3 + 2,84x^2 – 5,6064x – 14,766336 = 0
	x^3 + 1,41x^2 – 5,4724x – 7,3380384 = 0
	x^3 + 0,85x^2 – 0,4317x + 0,043911 = 0
	x^3 – 0,12x^2 – 1,4775x + 0,191906 = 0
	x^3 + 0,77x^22 – 0,2513x + 0,016995 = 0
	x^3 + 0,88x^2 – 0,3999x + 0,037638 = 0
	x^3 + 0,78x^2 – 0,8269x + 0,146718 = 0
	x^3 + 2,28x^2 – 1,9347x – 3,907574 = 0

		[0,2; 1]	0,5472
		[1; 2]	1,0769

 

Замечание. В вариантах 11 и 12 решается трансцендентное уравнение, которое имеет единственный корень на заданном отрезке. Поэтому локализация корней не требуется.

 

Лабораторная работа №4