Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расширение диапазона регулирования приводовСодержание книги
Поиск на нашем сайте
Как известно (см. п/п. 3.9.1.6), диапазон регулирования приводов с нормальными множительными структурами при двух передачах в последней множительной группе (pk=2) не может превышать величины 64/φ, что для большинства случаев явно недостаточно. Применение прогрессивных инструментальных материалов и покрытий обуславливает необходимость увеличения диапазона регулирования в универсальных станках. Однако желание увеличить диапазон регулирования при сохранении нормальной равномерной структуры приводит к нарушению граничных условий по передаточным отношениям (см. п/п. 3.9.1.5) в последней множительной группе. При необходимости увеличения диапазона регулирования без нарушения граничных условий в последней множительной группе можно применить ряд структур и в частности: - приводы с переборами; - структуры с перекрытием части ступеней скорости шпинделя; - структуры с составным геометрическим рядом; - приводы со сложенной структурой. Наиболее эффективно применение таких структур при pk=2.
3.9.6.1 Приводы с переборами (ступенями возврата)
Для увеличения редукции и диапазона регулирования в качестве последней множительной группы часто используют перебор (см. рис. 2.3,г и 2.11,а,б). Поскольку перебор обычно имеет две последовательные замедляющие передачи, то для него может быть imin=1/16, а т.к. imax=1, то диапазон регулирования перебора
Решение последнего выражения для ряда значений xmax дано на рис. 3.3,в. Поскольку перебор (ступень возврата) "возвращает" движение на ту же ось (на выходной вал, соосный с входным), то структурные сетки приводов с переборами строятся несимметрично. Для приводов по рис. 2.11 структурные сетки представлены на рис. 3.3. Проанализируем их: а) привод на 12 вариантов с одинарным перебором (см. рис. 2.11,а и 3.3,а)
При желании из каких либо соображений применить двойной перебор и допустимости меньшего числа вариантов структура, к примеру, 9=3(1)·3(3) лучше аналогичной нормальной. Для нее
Определение чисел зубьев колёс, образующих перебор, следует производить с учётом того, что модули передач перебора могут быть различными вследствие сильной редукции, осуществляемой первой передачей, и обусловленного этим значительного увеличения крутящего момента, передаваемого второй парой колёс. Модули обеих передач можно принять и одинаковыми за счёт более высокого качества материалов второй пары колёс или увеличения длины их зубьев.
3.9.6.2 Приводы с перекрытием (повторением) части ступеней скорости шпинделя
Для обеспечения перекрытия части ступеней скорости характеристику последней множительной группы уменьшают на несколько единиц. Рассмотрим получение структур с перекрытием при pk=2 на следующем примере. В структуре z = 16 = 4(1)·2(4)·2(8) с Д = 31,5 (т.к. Как видно, каждая из ступеней n5–n8 получается двумя комбинациями передач, в результате различных частот вращения фактически обеспечивается zф = z – zпер = 16 – 4 = 12, где zпер – количество перекрытых частот вращения. Развернутую структурную формулу можно представить в виде: zф=12=4(1)·2(4)·2(4). Диапазон регулирования привода с перекрытием:
Приравняв показатели степеней в первом и втором выражениях, получим zф = 0,5z + xk.пер, откуда xk.пер = zф – 0,5z и z = 2(zф – xk.пер). Для структур с перекрытием φmax следует определять в последней (k-той) и предпоследней (k–1) множительных группах и принимать φ не превосходящим меньшего из двух полученных значений φmax. В рассматриваемом случае xmax (k) = xmax (k-1) = 4,
Нормальная множительная структура на 12 вариантов z=12=3(1)·2(3)·2(6) (см. рис. 2.10) допускает Как видно, структура с перекрытием обеспечивает диапазон регулирования в 3,5 раза больший при тех же 12 фактических вариантах. Для этого потребовалось усложнить конструкцию по рис. 2.10 всего на одну передачу.
Для обеспечения в структуре с перекрытием максимального диапазона при заданных z и кинематической схеме следует принять φ =φmax при хk.пер = xmax (k-1). При этом, если φmax не равно какому-либо стандартному значению, то, приняв стандартное φ<φmax, следует проверить возможность увеличения хk.пер по формуле Покажем в качестве примера, как спроектировать структуры с максимальными диапазонами на базе приводов 12=3·2·2 и 24=4·3·2:
а) zф=3(1)·2(xk-1)·2(xk.пер.), zф=3(1)·2(3)·2(xk.пер.), т.к. pk-1 =2, xmax (k-1)=xk-1=3, то принимаем xk.пер =xmax (k-1) =3. Тогда
б) zф=4(1)·3(xk-1)·2(xk.пер), zф=4(1)·3(4)·2(xk.пер.), т.к. pk-1 Тогда
Из всех возможных структур с перекрытием максимальный диапазон обеспечивают:
т.е. диапазон может быть увеличен примерно в 8 раз по сравнению с тем, какой обеспечивается нормальной множительной структурой. Использование структур с перекрытием позволяет строить приводы практически на любые числа вариантов (10, 11,13, 14, 15, 17 и т.п.).
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 360; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.3.235 (0.006 с.) |



 Рис. 3.3. Варианты структурныхсеток приводов с переборами одинарным (а) и двойным (б) и таблица для определения φmax (в)
Рис. 3.3. Варианты структурныхсеток приводов с переборами одинарным (а) и двойным (б) и таблица для определения φmax (в)
 б) привод на 18 вариантов с двойным перебором (см. рис. 2.11,б и 3.3,б)
б) привод на 18 вариантов с двойным перебором (см. рис. 2.11,б и 3.3,б)

 В данном случае не обеспечивается выигрыша по диапазону в сравнении с нормальной множительной структурой
В данном случае не обеспечивается выигрыша по диапазону в сравнении с нормальной множительной структурой 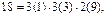 для которой
для которой 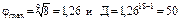 также.
Этот пример показывает, что не всякое решение даёт выигрыш, и всегда следует делать сравнительный анализ возможных вариантов.
также.
Этот пример показывает, что не всякое решение даёт выигрыш, и всегда следует делать сравнительный анализ возможных вариантов.
 в то время как нормальная структура допускает
в то время как нормальная структура допускает  что по величине обеспечиваемого диапазона значительно хуже.
что по величине обеспечиваемого диапазона значительно хуже. то при φ = 1,26 обеспечивается
то при φ = 1,26 обеспечивается  ) вместо xk= 8 примем xk.пер= 4 и рассмотрим построенную для этого случая структурную сетку (рис. 3.4).
) вместо xk= 8 примем xk.пер= 4 и рассмотрим построенную для этого случая структурную сетку (рис. 3.4).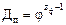 или (см. рис. 3.4)
или (см. рис. 3.4) 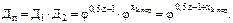
 и при φ =1,58 обеспечивается диапазон регулирования частот вращения шпинделя
и при φ =1,58 обеспечивается диапазон регулирования частот вращения шпинделя 
 и при φ =1,41 обеспечивает
и при φ =1,41 обеспечивает 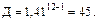
 полученной из выражения
полученной из выражения  (см. п/п. 3.9.1.7) для данного случая.
(см. п/п. 3.9.1.7) для данного случая.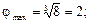 zф=12/2+3=9 и 9=3(1)·2(3)·2(3). При φ =2
zф=12/2+3=9 и 9=3(1)·2(3)·2(3). При φ =2 
 2, то xmax (k-1) = (pk-1–1) ·xk-1=(3–1)·4=8 и xk.пер=xmax(k-1)=8.
2, то xmax (k-1) = (pk-1–1) ·xk-1=(3–1)·4=8 и xk.пер=xmax(k-1)=8. zф=24/2+8=20. При φ =1,26
zф=24/2+8=20. При φ =1,26  Если принять xk.пер=lg8/lg1,26
Если принять xk.пер=lg8/lg1,26 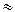 9, то zф=24/2+9=21=4(1)·3(4)·2(9) и
9, то zф=24/2+9=21=4(1)·3(4)·2(9) и