
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Значения чисел некоторых геометрических рядов в пределах 1- 9500Содержание книги
Поиск на нашем сайте
Продолжение табл. 3.6
Кинематический расчёт приводов станков
3.9.1 Основные определения и зависимости
Структура привода
Рассмотрим привод главного движения по рис. 2.10. В нём имеются ременная и зубчатая одиночные передачи и три группы передач "а", "б" и "в" с числами передач, соответственно, ра, рб и рв. Группа "а" имеет три передачи. Будем показывать это так: Передачи следующие:
Число ступеней частот вращения, обеспечиваемых приводом, z= 3·2·2 = 12, а в общем виде:
Последнее выражение называют структурной формулой привода. Структурная формула показывает: - какое количество частот вращения обеспечивается приводом; - сколько групп передач в нём; - число передач в каждой группе; - расположение каждой группы передач в приводе.
Примечание. количество групп передач при данном z, как и порядок расположения их, может быть различным. К примеру, если не задаваться кинематической схемой, то структуру привода можно принять: 12=4·3; 12= 3·2·2; 12= 2·3·2 и т.д.
Порядок переключения групп передач
Для получения последовательно возрастающего геометрического ряда частот вращения шпинделя в пределах nmin-nmax групповые передачи должны переключаться в определённом порядке. Группу передач, переключаемую в первую очередь, называют основной, во вторую – первой множительной (умножающей, переборной), в третью – второй множительной и т.д., если групп больше, чем три. В качестве основной, как и любой множительной можно запроектировать любую группу передач, независимо от её расположения в приводе и не меняя этого расположения. Если обозначить через рo основную группу, рI – I множительную, рII – II множительную, то в рассматриваемом случае возможны следующие варианты:
Очевидно, что число вариантов переключений равно числу перестановок групп.
Взаимосвязь передаточных отношений в группах передач привода
Примем для привода по рис. 2.10 порядок переключения групп
здесь I1, I2, I3,... – полные передаточные отношения привода;
Поскольку где φ – знаменатель геометрического ряда частот вращения шпинделя, то
- в основной группе будет обеспечиваться:
т.е. передаточные отношения в основной группе составляют геометрический ряд со знаменателем, равным знаменателю ряда частот вращения выходного вала привода φ; - в I множительной группе: здесь имеется геометрический ряд со знаменателем - во II множительной группе: здесь имеется геометрический ряд со знаменателем
В общем случае при числе передач в группе р:
т.е. передаточные отношения в каждой группе передач образуют геометрический ряд со знаменателем - для основной группы xо = 1; - для I множительной xI = pо; - для II множительной xII = pо·pI = xI· pI.
В общем случае для j-той множительной группы – Для последней (k-той) множительной группы –
т.е. характеристику последней множительной группы можно определить, зная число передач в ней и число вариантов скоростей, обеспечиваемых на шпинделе.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 187; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.236.101 (0.008 с.) |

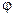 =1,06
=1,06

 причем
причем 
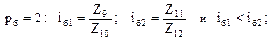

 и составим для этого случая план соединения шестерен. В рассматриваемой схеме будем считать, что
и составим для этого случая план соединения шестерен. В рассматриваемой схеме будем считать, что  , и это в нижеследующие записи не введём для их упрощения.
, и это в нижеследующие записи не введём для их упрощения.









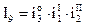
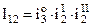
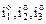 – передаточные отношения в основной группе;
– передаточные отношения в основной группе; – передаточные отношения в I множительной группе и т.д.
– передаточные отношения в I множительной группе и т.д.
 ,
, ,
,
 ,
,

 , где x, назовём его характеристикой группы передач, равен:
, где x, назовём его характеристикой группы передач, равен:
 Умножив правую часть последнего выражения на единицу в виде pk/pk, получим:
Умножив правую часть последнего выражения на единицу в виде pk/pk, получим: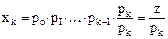 или
или  ,
,


