Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистическое моделирование случайных календарных графиковСодержание книги
Поиск на нашем сайте
На практике при определении статистических характеристик риска несвоевременного выполнения работ зачастую используют обобщенные (интегральные) характеристики. В частности, определяется, с какой вероятностью фактическая продолжительность работы будет превышать запланированную продолжительность. Для наиболее полного статистического описания используются различные функции распределения плотности вероятности f(t), показывающие вероятность выполнения работы, продолжительность которой находится в промежутке времени от t до t + D t. Выведем искомую функцию распределения плотности вероятности исходя из следующих утверждений: а) согласно закону Паркинсона, если работа выполнима за отведенное на нее плановое время - а, то ее выполнение заполнит все запланированное время. Из этого следует, что плотность вероятности досрочного выполнения работы будет равна нулю; б) плотность вероятности выполнения работы за большее время меньше, чем плотность вероятности выполнения работы за меньшее время. Из этого утверждения следует, что кривая, описывающая плотность вероятности, является монотонно убывающей функцией; в) считаем, что для монотонно убывающих функций уменьшение плотности вероятности во времени происходит за счет регулирующего воздействия исполнителя на прогнозируемое увеличение несвоевременности работы. Для определения следствия из утверждения в) проанализируем первую производную плотности вероятности по времени df(t)/dt, которая определяется как изменение скорости уменьшения плотности вероятности. Положим, что изменение скорости уменьшения плотности вероятности пропорционально самой плотности вероятности. Физически это соответствует тому, что большей несвоевременности соответствует большая управленческая сила возврата к планируемому значению. Формализованным результатом данных предположений является следующее дифференциальное уравнение:
где a - это коэффициент пропорциональности. Интегрируя уравнение (12), получаем экспоненциальную функцию распределения плотности вероятности, которую, при нормировке параметров, можно представить в следующем виде
г) считаем, что максимальное время несвоевременного выполнения работы является конечной величиной - в. Из этого следует, что плотность вероятности несвоевременного выполнения работы для продолжительности выше этого предела равна нулю; Как видно из формулы (13), полученное распределение не ограничено максимальным значением. Поэтому для реализации предложения г) принимаем, что математическое ожидание составляет одну четвертую от условного размаха продолжительностей [ a, b ]. И тогда формула (13) трансформируется к следующему виду:
В результате получено, что экспоненциальное распределение разделено на квартили равные ширине стандартного отклонения, а математическое ожидание будет делить размах в отношении один к трем. В таком представлении экспоненциальное распределение будет обеспечивать корректную генерацию более 99% значений случайных продолжительностей работ в диапазоне от планового значения - а до значения максимальной несвоевременности - в. Поскольку в программе МР используется равномерный генератор случайных чисел (от 0 до 1) Rnd, то формула перехода от равномерного генератора к экспоненциальному распределению имеет следующий вид
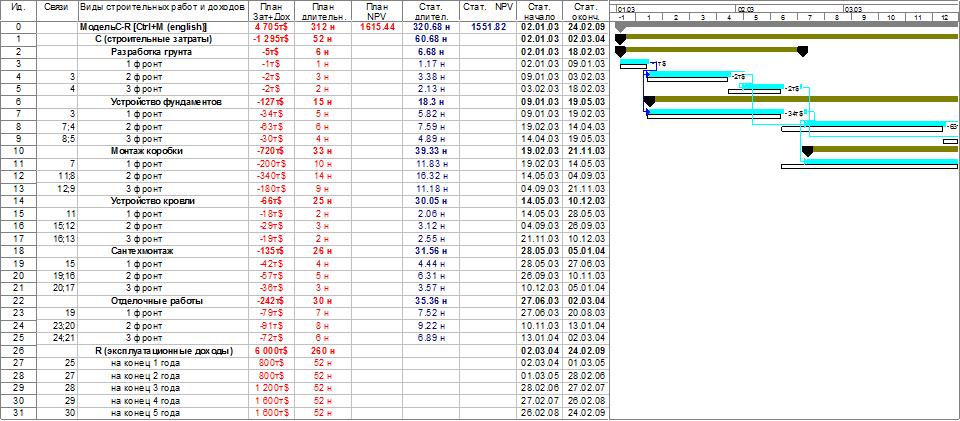
Пример, демонстрирующий статистическое моделирование случайных календарных графиков в программе МР, показан на рис.9. Алгоритм реализации сводится к следующим основным процедурам. 1. Формируется календарный график, в котором все плановые характеристики детерминированного календарного графика определяются программой как базовые характеристики. 2. В любой из пользовательских столбцов, определенных программой как «Продолжительность1», «Продолжительность2», «Продолжительность3» и т.п., вводится следующая формула
(16) где Ind – максимальный индекс несвоевременности работ, используемый как константа для всех работ, а – плановая продолжительность находится в столбце «Базовая продолжительность». 3. Из пользовательского столбца, в который внесена формула (16) рассчитываются (в МР, нажатием клавиши F 9) и копируются данные в стандартный столбец «Продолжительность»
Рис.9 Пример статистического моделирования календарных планов в программе МР.
4. МР автоматически (как правило) пересчитывает все расписание работ, которое после введения случайных работ является стохастическим, и отображает его в выбранной форме календарного графика, как правило, графика Ганта. 5. Для расчета чистого дисконтированного дохода (NPV) стохастического и детерминированного денежных потоков вводятся стоимости всех работ и параметры доходного периода. 6. Для вычисления NPV используется формула (6), которая вводится в любые пользовательские столбцы, с названиями «Затраты1», «Затраты2», «Затраты3» и т.п. 7. Для набора необходимой статистики расчет новых случайных продолжительностей и их копирование в столбец «Продолжительность» повторяется.
Контрольные вопросы 1. В чем заключается основное отличие субъективных и объективных причин возникновения несвоевременности выполнения работ. 2. Почему принятие гипотезы о равномерности выполнения работы приводит к несвоевременности? 3. Какое распределение случайной продолжительности используется в методе PERT. 4. В чем Вы видите отличие метода от метода статистического моделирования? 5. С какими исходными положениями связано экспоненциальное распределение случайной продолжительности работы. Лекция 6. Организация строительной площадки
Содержание лекции 6.1 Основы организации строительной площадки и роль заказчика 6.2 Роль подрядчика на строительной площадке 6.3 Временные здания, сооружения и инженерные сети 6.4 Проектирование строительной площадки в программах BIM моделирования
|
||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 275; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.28.217 (0.005 с.) |

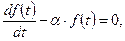 (12)
(12)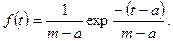 (13)
(13) (14)
(14) (15)
(15)