Реализация очереди на базе массива

Как уже было сказано, программисту массив дан свыше, все остальные структуры данных нужно реализовывать на его основе. Конечно, такая реализация может быть многоэтапной, и не всегда массив выступает в качестве непосредственной базы реализации. В случае очереди наиболее популярны две реализации: непрерывная на базе массива, которую называют также реализацией на базе кольцевого буфера, и ссылочная реализация, или реализация на базе списка. Ссылочные реализации будут рассмотрены ниже.

При непрерывной реализации очереди в качестве базы выступает массив фиксированной длины N, таким образом, очередь ограничена и не может содержать более N элементов. Индексы элементов массива изменяются в пределах от 0 до N - 1. Кроме массива, реализация очереди хранит три простые переменные: индекс начала очереди, индекс конца очереди, число элементов очереди. Элементы очереди содержатся в отрезке массива от индекса начала до индекса конца.

При добавлении нового элемента в конец очереди индекс конца сперва увеличивается на единицу, затем новый элемент записывается в ячейку массива с этим индексом. Аналогично, при извлечении элемента из начала очереди содержимое ячейки массива с индексом начала очереди запоминается в качестве результата операции, затем индекс начала очереди увеличивается на единицу. Как индекс начала очереди, так и индекс конца при работе двигаются слева направо. Что происходит, когда индекс конца очереди достигает конца массива, т.е. N - 1?

Ключевая идея реализации очереди состоит в том, что массив мысленно как бы зацикливается в кольцо. Считается, что за последним элементом массива следует его первый элемент (напомним, что последний элемент имеет индекс N - 1, а первый — индекс 0). При сдвиге индекса конца очереди вправо в случае, когда он указывает на последний элемент массива, он переходит на первый элемент. Таким образом, непрерывный отрезок массива, занимаемый элементами очереди, может переходить через конец массива на его начало.

Для реализации очереди используют две индексные переменные:

head, указывающая первый элемент очереди, который будет удален из нее операцией Dequeue;

tail, указывающая позицию, в которую будет добавляться новый элемент при помощи Enqueue.

Если очередь пуста head= tail (изначально head= tail=1), то при попытки удалить из нее элемент происходит ошибка опустошения.

Если же очередь заполнена, то попытка добавить в нее элемент приводит к ее переполнению.

Enqueue(S,x)

S[tail]=x

If tail=n-1 then tail=0

Else tail=tail+1

End

 

Dequeue(S)

X=S[head]

If head=n-1 then head=0

Else head=head+1

Return x

End

 

В псевдокодах нет проверки на ошибки переполнения и опустошения – добавьте.

Ссылочные реализации структур данных

Большинство структур данных реализуется на базе массива. Все реализации можно разделить на два класса: непрерывные и ссылочные. В непрерывных реализациях элементы структуры данных располагаются последовательно друг за другом в непрерывном отрезке массива, причем порядок их расположения в массиве соответствует их порядку в реализуемой структуре. Рассмотренные выше реализации очереди и стека относятся к непрерывным.

В ссылочных реализациях элементы структуры данных хранятся в произвольном порядке. При этом вместе с каждым элементом хранятся ссылки на один или несколько соседних элементов. В качестве ссылок могут выступать либо индексы ячеек массива, либо адреса памяти. Можно представить себе шпионскую сеть, в которой каждый участник знает лишь координаты одного или двух своих коллег. Контрразведчикам, чтобы обезвредить сеть, нужно пройти последовательно по всей цепочке, начиная с выявленного шпиона.

Ссылочные реализации обладают двумя ярко выраженными недостатками: 1) для хранения ссылок требуется дополнительная память; 2) для доступа к некоторому элементу структуры необходимо сначала добраться до него, проходя последовательно по цепочке других элементов. Казалось бы, зачем нужны такие реализации?

Все недостатки ссылочных реализаций компенсируются одним чрезвычайно важным достоинством: в них можно добавлять и удалять элементы в середине структуры данных, не перемещая остальные элементы.

Массовые операции

Массовые операции — это операции, затрагивающие значительную часть всех элементов структуры данных. Пусть нужно добавить или удалить один элемент. Если при этом приходится, например, переписывать значительную часть остальных элементов с одного места на другое, то говорят, что добавление или удаление приводит к массовым операциям. Массовые операции — это бедствие для программиста, то, чего он всегда стремится избежать. Хорошая реализация структуры данных — та, в которой массовых операций либо нет совсем, либо они происходят очень редко. Например, добавление элемента должно выполняться за ограниченное число шагов, независимо от того, содержит ли структура десять или десять тысяч элементов.

В непрерывных реализациях добавление или удаление элементов в середине структуры неизбежно приводит к массовым операциям. Поэтому структуры, в которых можно удалять или добавлять элементы в середине, обязательно должны быть реализованы ссылочным образом.

Пример неудачного использования непрерывных реализаций — файловые системы в некоторых старых операционных системах, например, в уже упомянутой ОС ЕС или в системе РАФОС, применявшейся на СМ ЭВМ, на старых советских персональных компьютерах Электроника и т.п. В современных файловых системах файлы фрагментированы, т.е. кусочки большого файла, непрерывного с точки зрения пользователя, на самом деле могут быть разбросаны по всему диску. Раньше это было не так, файлы должны были обязательно занимать непрерывный участок на диске. При постоянной работе файлы уничтожались и создавались заново на новом месте — и всякое редактирование текстового файла приводило к его обновлению. В результате свободное пространство на диске становилось фрагментированным, т.е. состоящим из множества небольших кусков. Возникала ситуация, когда большой файл невозможно записать на диск: хотя свободного места в сумме много, нет достаточно большого свободного фрагмента. Приходилось постоянно выполнять длительную и опасную процедуру сжатия диска, которая часто приводила к потере всех данных на нем.

 

Списки

Связанный список – это структура, в которой объекты расположены в линейном порядке. Однако, в отличие от массива, в котором это порядок определяется индексами, порядок в связанном списке определяется указателями на объекты.

Элемент (узел) связанного списка помимо поля данных имеет поле Next, в котором содержится указатель на следующий элемент списка (если это последний элемент списка, то поле Next принимает нулевое значение nill). Каждый список содержит указатель head на первый элемент списка. Если этот указатель равен 0, то список пуст.

Приведем примеры различных списочных структур:

• a)Односвязный (линейный) список: структура, каждый элемент которой "знает" адрес только следующего за ним элемента (см. рис. 1.(a)). Очень удобно представлять таким списком стек и очередь. По односвязному списку можно пройти только в одном направлении: от начала к концу.
• b)Двусвязный линейный список: структура, каждый элемент которой "помнит" адрес не только следующего Next, но и предыдущего элемента Prev списка (см. рис. 1.(b)). Этот список удобен для работы с деками. В этом списке можно перемещаться в двух направлениях. Частый случай такого списка – замкнутый (кольцевой) список, указатель next последнего элемента которого ссылается на первый элемент, а указатель prev первого элемента на последний элемент списка.
• c)Бинарное дерево может быть представлено двусвязным нелинейным списком: каждая вершина помнит обоих своих возможных потомков (см. рис. 1. (c)). Если каждой вершине необходимо помнить не только потомков, но и предка, то список становится трехсвязным.
• d) Для представления ориентированного графа можно использовать иерархические списки - комбинацию из двух различных линейных списков (см. рис. 1(d): вершины задаются структурой, содержащей три поля, а дуги - два; справа показан орграф, представленный приведенной списочной структурой).

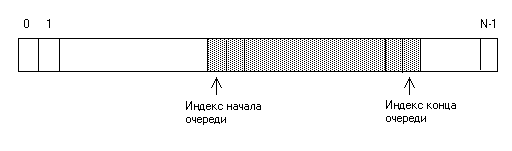
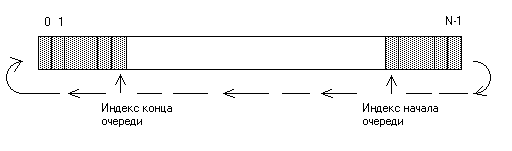
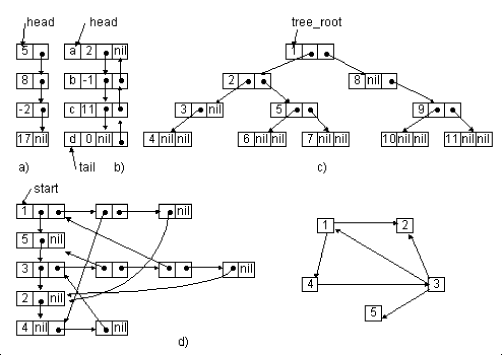рисунок 1