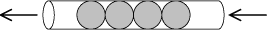Стековый калькулятор и обратная польская запись формулы

В 1920 г. польский математик Ян Лукашевич предложил способ записи арифметических формул, не использующий скобок. В привычной нам записи знак операции записывается между аргументами, например, сумма чисел 2 и 3 записывается как 2 + 3. Ян Лукашевич предложил две другие формы записи: префиксная форма, в которой знак операции записывается перед аргументами, и постфиксная форма, в которой знак операции записывается после аргументов. В префиксной форме сумма чисел 2 и 3 записывается как + 2 3, в постфиксной — как 2 3 +. В честь Яна Лукашевича эти формы записи называют прямой и обратной польской записью.

В польской записи скобки не нужны. Например, выражение

(2+3)*(15-7)

записывается в прямой польской записи как

* + 2 3 - 15 7,

в обратной польской записи — как

2 3 + 15 7 - *.

Если прямая польская запись не получила большого распространения, то обратная оказалась чрезвычайно полезной. Неформально преимущество обратной записи перед прямой польской записью или обычной записью можно объяснить тем, что гораздо удобнее выполнять некоторое действие, когда объекты, над которыми оно должно быть совершено, уже даны.

Обратная польская запись формулы позволяет вычислять выражение любой сложности, используя стек как запоминающее устройство для хранения промежуточных результатов. Такой стековый калькулятор был впервые выпущен фирмой Hewlett Packard. Обычные модели калькуляторов не позволяют вычислять сложные формулы без использования бумаги и ручки для записи промежуточных результатов. В некоторых моделях есть скобки с одним или двумя уровнями вложенности, но более сложные выражения вычислять невозможно. Также в обычных калькуляторах трудно понять, как результат и аргументы перемещаются в процессе ввода и вычисления между регистрами калькулятора. Калькулятор обычно имеет регистры X, Y и регистр памяти, промежуточные результаты каким-то образом перемещаются по регистрам, каким именно — запомнить невозможно.

В отличие от других калькуляторов, устройство стекового калькулятора вполне понятно и легко запоминается. Калькулятор имеет память в виде стека. При вводе числа оно просто добавляется в стек. При нажатии на клавишу операции, например, на клавишу +, аргументы операции сначала извлекаются из стека, затем с ними выполняется операция, наконец, результат операции помещается обратно в стек. Таким образом, при выполнении операции с двумя аргументами, например, сложения, в стеке должно быть не менее двух чисел. Аргументы удаляются из стека и на их место кладется результат, то есть при выполнении сложения глубина стека уменьшается на единицу. Вершина стека всегда содержит результат последней операции и высвечивается на дисплее калькулятора.

Для вычисления выражения надо сначала преобразовать его в обратную польскую запись (при некотором навыке это легко сделать в уме). В приведенном выше примере выражение (2+3)*(15-7) преобразуется к

2 3 + 15 7 - *

Затем обратная польская запись просматривается последовательно слева направо. Если мы видим число, то просто вводим его в калькулятор, т.е. добавляем его в стек. Если мы видим знак операции, то нажимаем соответствующую клавишу калькулятора, выполняя таким образом операцию с числами на вершине стека.

Изобразим последовательные состояния стека калькулятора при вычислении по приведенной формуле. Сканируем слева направо ее обратную польскую запись:

2 3 + 15 7 - *

Стек вначале пуст. Последовательно добавляем числа 2 и 3 в стек.

| | вводим число 2 | 2 | вводим число 3 | 3 |

Далее читаем символ + и нажимаем на клавишу + калькулятора. Числа 2 и 3 извлекаются из стека, складываются, и результат помещается обратно в стек.

выполняем сложение | 5 |

Далее, в стек добавляются числа 15 и 7.

| 5 | вводим число 15 | 15 | вводим число 7 | 7 |

Читаем символ - и нажимаем на клавишу - калькулятора. Со стека при этом снимаются два верхних числа 7 и 15 и выполняется операция вычитания. Причем уменьшаемым является то число, которое было введено раньше, а вычитаемым — число, введенное позже. Иначе говоря, при выполнении некоммутативных операций, таких как вычитание или деление, правым аргументом является число на вершине стека, левым — число, находящееся под вершиной стека.

выполняем вычитание | 8 |

Наконец, читаем символ * и нажимаем на клавишу * калькулятора. Калькулятор выполняет умножение, со стека снимаются два числа, перемножаются, результат помещается обратно в стек.

| 8 | выполняем умножение | 40 ||

Число 40 является результатом вычисления выражения. Оно находится на вершине стека и высвечивается на дисплее стекового калькулятора.

Польская запись присутствует и в обычных вычислениях: запись функций - прямая польская запись sin(x), а вычисление факториала n!- обратная.

Очередь

Очередь как структура данных понятна даже людям, не знакомым с программированием. Очередь содержит элементы, как бы выстроенные друг за другом в цепочку. У очереди есть начало и конец. Добавлять новые элементы можно только в конец очереди, забирать элементы можно только из начала, т.е. действует принцип: Первый вошел- первый вышел FIFO. В отличие от обычной очереди, которую всегда можно при желании покинуть, из середины программистской очереди удалять элементы нельзя.

Очередь можно представить в виде трубки. В один конец трубки можно добавлять шарики — элементы очереди, из другого конца они извлекаются. Элементы в середине очереди, т.е. шарики внутри трубки, недоступны. Конец трубки, в который добавляются шарики, соответствует концу очереди, конец, из которого они извлекаются — началу очереди. Таким образом, концы трубки не симметричны, шарики внутри трубки движутся только в одном направлении.

В принципе, можно было бы разрешить добавлять элементы в оба конца очереди и забирать их также из обоих концов. Такая структура данных в программировании тоже существует, ее название — "дек", от англ. Double Ended Queue, т.е. очередь с двумя концами. Дек применяется значительно реже, чем очередь.

Использование очереди в программировании почти соответствует ее роли в обычной жизни. Очередь практически всегда связана с обслуживанием запросов, в тех случаях, когда они не могут быть выполнены мгновенно. Очередь поддерживает также порядок обслуживания запросов. Рассмотрим, к примеру, что происходит, когда человек нажимает клавишу на клавиатуре компьютера. Тем самым человек просит компьютер выполнить некоторое действие. Например, если он просто печатает текст, то действие должно состоять в добавлении к тесту одного символа и может сопровождаться перерисовкой области экрана, прокруткой окна, переформатированием абзаца и т.п.

Любая, даже самая простая, операционная система всегда в той или иной степени многозадачная. Это значит, что в момент нажатия клавиши операционная система может быть занята какой-либо другой работой. Тем не менее, операционная система ни в какой ситуации не имеет права проигнорировать нажатие на клавишу. Поэтому происходит прерывание работы компьютера, он запоминает свое состояние и переключается на обработку нажатия, на клавишу. Такая обработка должна быть очень короткой, чтобы не нарушить выполнение других задач. Команда, отдаваемая нажатием на клавишу, просто добавляется в конец очереди запросов, ждущих своего выполнения. После этого прерывание заканчивается, компьютер восстанавливает свое состояние и продолжает работу, которая была прервана нажатием на клавишу. Запрос, поставленный в очередь, будет выполнен не сразу, а только когда наступит его черед.

В системе Windows работа оконных приложений основана на сообщениях, которые посылаются этим приложениям. Например, бывают сообщения о нажатии на клавишу мыши, о закрытии окна, о необходимости перерисовки области окна, о выборе пункта меню и т.п. Каждая программа имеет очередь запросов. Когда программа получает свой квант времени на выполнение, она выбирает очередной запрос из начала очереди и выполняет его. Таким образом, работа оконного приложения состоит, упрощенно говоря, в последовательном выполнении запросов из ее очереди. Очередь поддерживается операционной системой.

Подход к программированию, состоящий не в прямом вызове процедур, а в посылке сообщений, которые ставятся в очередь запросов, имеет много преимуществ и является одной из черт объектно-ориентированного программирования. Так, например, если оконной программе необходимо завершить работу по какой-либо причине, лучше не вызывать сразу команду завершения, которая опасна, потому что нарушает логику работы и может привести к потере данных. Вместо этого программа посылает самой себе сообщение о необходимости завершения работы, которое будет поставлено в очередь запросов и выполнено после запросов, поступивших ранее.