
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Графики классов расчетных нагрузок 1896-1925 гг.Содержание книги
Поиск на нашем сайте
В ЕДИНИЦАХ ЭТАЛОННОЙ НАГРУЗКИ H1.
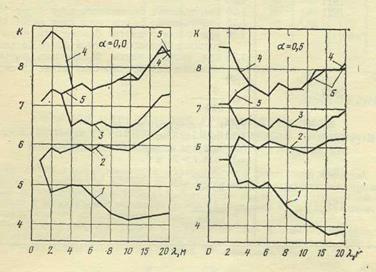
Рис. Расчетные нагрузки: 1-1896 г; 2-1907 г; 3-1927 г; 4-1923 г; 5-1925 г.
ПРИЛОЖЕНИЕ 8 ДИНАМИЧЕСКИЕ КОЭФФИЦИЕНТЫ И ДОПУСКАЕМЫЕ НАПРЯЖЕНИЯ ПО СТАРЫМ НОРМАМ ПРОЕКТИРОВАНИЯ Таблица 1. Величины динамических коэффициентов
Таблица 2. Допускаемые напряжения для арматуры
Таблица 3. Допускаемые напряжения в бетоне на сжатие при изгибе
ПРИЛОЖЕНИЕ 9 ПРИМЕР ОПРЕДЕЛЕНИЯ ГРУЗОПОДЪЕМНОСТИ ПРОЛЕТНОГО СТРОЕНИЯ С НЕНАПРЯГАЕМОЙ АРМАТУРОЙ НА ОСНОВЕ СОПОСТАВЛЕНИЯ РАСЧЕТНЫХ НОРМ Определим грузоподъемность двухребристого пролетного строения проектировки Гипротранса в 1931 г. под нагрузку H7 с расчетным пролетом l=10,8 м, построенного в 1933 г. Расчет этого пролетного строения по опалубочным и арматурным чертежам дан в приложении 6, где приведены также результаты его обследования. Поскольку пролетное строение запроектировано в 1931 г., принято, что расчет его выполнялся в соответствии с техническими условиями 1931 г. 1. Расчет плиты балластного корыта. Коэффициент
где Rs =190 Мпа – расчетное сопротивление ненапрягаемой арматуры; Ra =130 МПа – допускаемое напряжение для арматуры по нормам 1931 г.; i= 1 – относительное изменение площади сечения арматуры. Допускаемая временная нагрузка для монолитного участка плиты между ребрами
где Kн =7 – класс временной нагрузки, на которую рассчитывалось пролетное строение в единицах эталонной нагрузки H7; Остальные величины приведены в приложении 6. Класс по прочности для монолитного участка плиты между ребрами:
где kн =27,3 кН/м; Допускаемая временная нагрузка для сечения III-III.
где Mp =12,71 кНм – изгибающий момент от постоянных нагрузок для сечения III-III при расчете на прочность (см. приложение 6): Класс по прочности консоли плиты в сечении III-III 2. Расчет главной балки. Допускаемая временная нагрузка для сечения А-А.
где m =2 – число балок, воспринимающих нагрузку с одного пути; Остальные величины приведены в приложении 6. Класс по прочности главной балки в сечении А-А.
Сечение Б-Б. Относительное изменение площади сечения рабочей арматуры:
где n=14 - число стержней рабочей арматуры в элементе; n1 =4 – число стержней, поврежденных коррозией; n2 =0 – число стержней, выключенных из работы; Коэффициент Допускаемая временная нагрузка:
Класс по прочности главной балки в сечении Б-Б ПРИЛОЖЕНИЕ 10 УЧЕТ ВЛИЯНИЯ ДЕФЕКТОВ ПРОЛЕТНОГО СТРОЕНИЯ В РАСЧЕТАХ НА ВЫНОСЛИВОСТЬ. 1. Учет трещин в сжатой зоне. Учет влияния трещин, заходящих в сжатую зону бетона, при расчетах на выносливость производят следующим образом. Если высота сжатой зоны бетона Если высота сжатой зоны
где а) для прямоугольного сечения, а также для таврового сечения при
б) для таврового сечения при
Изгибающий момент от постоянной нагрузки Mp определяют по формуле (4.22) при Расчет сечений по выносливости арматуры с учетом трещин, заходящих в сжатую зону, не производят. 2. Учет наклонных трещин. Если при обследовании пролетного строения обнаружены наклонные трещины в стенке главной балки, то следует определить классы пролетного строения по выносливости хомутов и отгибов, пересеченных трещиной. Для расчета выбирают хомут или отгиб в месте, где трещина имеет наибольшую ширину. Производят испытание пролетного строения, при котором должны быть получены следующие данные:
Q – поперечная сила от испытательной нагрузки в сечении у конца трещины в сжатой зоне, приходящейся на рассчитываемый элемент (одну балку). Напряжения в хомуте или отгибе от испытательной нагрузки определяют по формуле:
где где
Предельная поперечная сила по выносливости арматурного стержня в месте пересечения его трещиной определяется по формулам: а) для пролетного строения с ненапрягаемой арматурой
б) для пролетного строения с напрягаемой арматурой (без преднапряженных хомутов)
где Допускаемую временную нагрузку по выносливости определяют по формуле
где Qp – поперечная сила от постоянных нагрузок, определяемая по формуле (4.27) при 3. Учет поперечных трещин в бетоне пролетных строений с напрягаемой арматурой. Сначала определяют предварительное напряжение в арматуре
где M – изгибающий момент в сечении с трещиной, для которого производились измерения, от постоянной и временной испытательной нагрузки; В расчеты на выносливость вводят величину по выносливости бетона
по выносливости арматуры
где Rbf, Rpf – расчетные сопротивления бетона и напрягаемой арматуры при расчете элементов на выносливость. Коэффициенты асимметрии цикла напряжений для расчетов по выносливости бетона и арматуры разрешается принимать соответственно Предельный изгибающий момент при расчете: по выносливости бетона
по выносливости арматуры
Допускаемая временная нагрузка по выносливости
где M – наименьший изгибающий момент из Остальные величины см. в п. 4.6. 4. Учет трещин, отделяющих плиту от стенки. При наличии в главной балке горизонтальной трещины, отделяющей плиту от стенки, следует определить класс пролетного строения по выносливости хомутов, пересекающих трещину. Для расчета выбирают хомут, пересекающий трещину в месте наибольшего ее раскрытия. Должно быть испытано пролетное строение (см. п. 8.10) и получены следующие данные:
q – равномерно распределенная нагрузка на плиту в месте измерения перемещения кромки трещины, определяемая по формуле q=k0/l0, где k0 и l0 определяют по формулам (7.2) и (4.6);
Допускаемая временная нагрузка по выносливости
где Rsf – расчетное сопротивление арматуры;
Остальные величины см. в п. 2. 5. Учет раковин и сколов бетона. Положение нейтральной оси определяют по формулам: для прямоугольного сечения
для таврового сечения
Момент инерции приведенного (к бетону) сечения, ослабленного раковиной или сколом,
где Ired – приведенный момент инерции, определяемый по формуле (4.40) или (4.44) с заменой Предельные изгибающие моменты определяют по формулам: по выносливости бетона
по выносливости арматуры
ПРИЛОЖЕНИЕ 11
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 281; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.74.192 (0.007 с.) |


 где l – расчетный пролет
1,30 при
где l – расчетный пролет
1,30 при  м;
1,20 при 5 м
м;
1,20 при 5 м 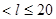 м;
1,10 при l>20 м
м;
1,10 при l>20 м
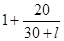 , но не больше 1,50
, но не больше 1,50

 марочной прочности
марочной прочности
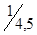 марочной прочности
марочной прочности
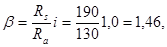

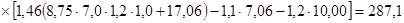 кН/м,
кН/м,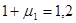 - динамический коэффициент при 5 м< l
- динамический коэффициент при 5 м< l 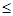 20 м – по нормам 1931 г. (см. приложение 8);
20 м – по нормам 1931 г. (см. приложение 8);  кН/м – постоянная нагрузка на монолитный участок плиты между ребрами.
кН/м – постоянная нагрузка на монолитный участок плиты между ребрами.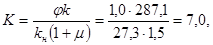
 .
.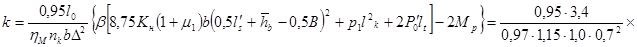
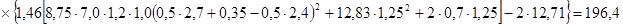 кН/м,
кН/м, м – длина шпалы, принятая при проектировании;
м – длина шпалы, принятая при проектировании;  м – толщина слоя балласта под шпалами, принятая при проектировании; p1 =4,66+8,17=12,83 кНм – постоянная нагрузка на консоли плиты;
м – толщина слоя балласта под шпалами, принятая при проектировании; p1 =4,66+8,17=12,83 кНм – постоянная нагрузка на консоли плиты;  кН – нагрузка от веса перил вдоль оси моста. Остальные величины приведены в приложении 6.
кН – нагрузка от веса перил вдоль оси моста. Остальные величины приведены в приложении 6.

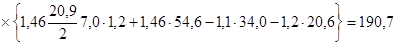 кН/м,
кН/м,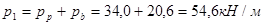 - постоянная нагрузка на балку.
- постоянная нагрузка на балку.

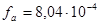 м2 – площадь сечения стержня, не поврежденного коррозией;
м2 – площадь сечения стержня, не поврежденного коррозией; 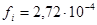 м2 – площадь ослабления сечения i- го стержня коррозией.
м2 – площадь ослабления сечения i- го стержня коррозией.
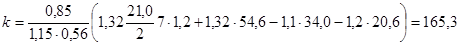 кН/м.
кН/м.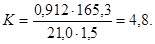
 (см. п. 6.4) больше, чем величина
(см. п. 6.4) больше, чем величина 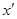 , вычисленная в соответствии с указаниями пп. 4.10, 4.11, то допускаемую временную нагрузку на выносливость бетона и арматуры определяют по формулам раздела 4.
, вычисленная в соответствии с указаниями пп. 4.10, 4.11, то допускаемую временную нагрузку на выносливость бетона и арматуры определяют по формулам раздела 4.

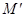 - предельный изгибающий момент, определяемый по формулам:
- предельный изгибающий момент, определяемый по формулам:
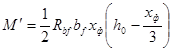 ;
;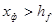
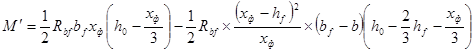 ;
; - коэффициент уменьшения динамического воздействия временной нагрузки, принимаемый по приложению 4.
- коэффициент уменьшения динамического воздействия временной нагрузки, принимаемый по приложению 4. . Остальные величины см. в п. 4.6.
. Остальные величины см. в п. 4.6. - изменение раскрытия трещины в месте пересечения её хомутом или отгибом под испытательной нагрузкой, измеренное перпендикулярно трещине;
- изменение раскрытия трещины в месте пересечения её хомутом или отгибом под испытательной нагрузкой, измеренное перпендикулярно трещине;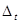 - сдвиг кромок трещины в том же месте и под той же нагрузки;
- сдвиг кромок трещины в том же месте и под той же нагрузки;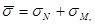
 ;
;  ,
,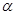 - угол направлением трещины и стержнем; Es – модуль упругости арматуры, кгс/см2; d – диаметр стержня, см; Ia – момент инерции сечения стержня, см4; R – марка бетона, кгс/см2; ap – условная длина арматурного стержня, принимаемая равной 9 диаметрам для арматуры периодического профиля и 13 диаметрам для гладкой арматуры;
- угол направлением трещины и стержнем; Es – модуль упругости арматуры, кгс/см2; d – диаметр стержня, см; Ia – момент инерции сечения стержня, см4; R – марка бетона, кгс/см2; ap – условная длина арматурного стержня, принимаемая равной 9 диаметрам для арматуры периодического профиля и 13 диаметрам для гладкой арматуры;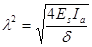 ;
;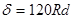 .
.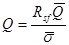 ;
;
 - условная площадь; Sred, Ired – статический момент полусечения и момент приведенного сечения балки; b – толщина ребра;
- условная площадь; Sred, Ired – статический момент полусечения и момент приведенного сечения балки; b – толщина ребра;  - предварительное напряжение в бетоне стенки на уровне нейтральной оси сечения;
- предварительное напряжение в бетоне стенки на уровне нейтральной оси сечения; 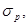
 - предварительное напряжение в арматуре и площадь ее поперечного сечений; Ared – приведенная площадь поперечного сечения балки.
- предварительное напряжение в арматуре и площадь ее поперечного сечений; Ared – приведенная площадь поперечного сечения балки.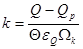 ,
, - доля временной нагрузки, определяемая по пп. 3.7-3.8;
- доля временной нагрузки, определяемая по пп. 3.7-3.8; 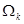 - площадь линии влияния поперечной силы, определяемая по формуле (4.26).
- площадь линии влияния поперечной силы, определяемая по формуле (4.26). , действующее при приложении к пролетному строению нагрузки, снижающей до нуля предварительное напряжение в нижней фибре бетона. Величину
, действующее при приложении к пролетному строению нагрузки, снижающей до нуля предварительное напряжение в нижней фибре бетона. Величину 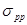 , устанавливаемую на основании результатов испытания пролетного строения, при которой измеряют относительные деформации бетона в сечении с трещиной и определяют высоту сжатой зоны, находят по формуле
, устанавливаемую на основании результатов испытания пролетного строения, при которой измеряют относительные деформации бетона в сечении с трещиной и определяют высоту сжатой зоны, находят по формуле ,
, , здесь Ap – площадь сечения рабочей арматуры, b – толщина ребра;
, здесь Ap – площадь сечения рабочей арматуры, b – толщина ребра; 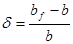 , здесь bf – ширина плиты;
, здесь bf – ширина плиты; 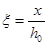 , здесь x – высота сжатой зоны бетона, полученная при испытании; h0 – рабочая высота сечения;
, здесь x – высота сжатой зоны бетона, полученная при испытании; h0 – рабочая высота сечения; 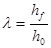 , здесь hf – толщина плиты; n1=Ep/Eb – отношение модулей упругости арматуры и бетона.
, здесь hf – толщина плиты; n1=Ep/Eb – отношение модулей упругости арматуры и бетона.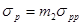 , где коэффициент условий работы m2 =0,8 при расчете по выносливости арматуры. Далее определяют относительную высоту сжатой зоны бетона в предельном состоянии
, где коэффициент условий работы m2 =0,8 при расчете по выносливости арматуры. Далее определяют относительную высоту сжатой зоны бетона в предельном состоянии  и
и 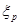 из уравнений:
из уравнений: ;
; ,
,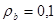 ;
; 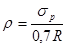 , где Rp – расчетное сопротивление напрягаемой арматуры при расчете на прочность (см. табл. 2.2).
, где Rp – расчетное сопротивление напрягаемой арматуры при расчете на прочность (см. табл. 2.2). ;
;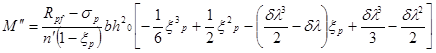 .
. ,
,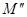 ; Mp – изгибающий момент от постоянной нагрузки, определяемый по формуле (4.22) при
; Mp – изгибающий момент от постоянной нагрузки, определяемый по формуле (4.22) при  - равномерно распределенная эквивалентная нагрузка от испытательного поезда по длине загружения, соответствующей загружаемому участку линии влияния поперечной силы для сечения у места измерений и при
- равномерно распределенная эквивалентная нагрузка от испытательного поезда по длине загружения, соответствующей загружаемому участку линии влияния поперечной силы для сечения у места измерений и при  .
. ,
, - площади линии влияния поперечной силы для сечения у места измерений, загружаемые соответственно временной и постоянной нагрузками;
- площади линии влияния поперечной силы для сечения у места измерений, загружаемые соответственно временной и постоянной нагрузками; ;
;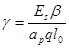 ;
; - отношение эталонной эквивалентной нагрузки на плиту к эталонной нагрузке при загружении площади линии влияния
- отношение эталонной эквивалентной нагрузки на плиту к эталонной нагрузке при загружении площади линии влияния 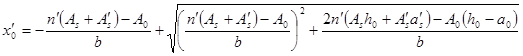 ;
;
 ,
, ,
,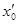 .
.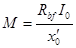 ;
; .
.


