
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчетные характеристики материаловСодержание книги
Поиск на нашем сайте
Бетон 2.1. Расчетные сопротивления бетона приведены в табл. 2.1 в зависимости от фактической прочности бетона, определяемой при обследовании (см. п. 8.9) расчетные сопротивления определяются по интерполяции. Расчетные сопротивления бетона сжатию в расчетах элементов на выносливость следует вычислять по формуле
где
и менее более
Модули упругости бетона
R, Мпа (кгс/см2) 25,0 (250) 30,0 40,0 50,0 60,0 и менее (300) (400) (500) (600) см2 27,0 29,5 33,5 36,0 38,5
Таблица 2.1. Расчетные сопротивления бетона
Примечания. 1. При классификации пролетных строений мостов, эксплуатируемых при расчетной минимальной температуре воздуха ниже минус 400С, табличные значения следует умножать на коэффициент условий работы 0,9. 2. Расчетную минимальную температуру воздуха определяют согласно указаниям СниП 2.05.03-84.
Арматура 2.2. Расчетные сопротивления ненапрягаемой стержневой арматуры растяжению Rs и сжатию Rsc, Мпа (кгс/см2), при расчете элементов на прочность:
Арматура гладкая 190 (1900) Арматура периодического профиля 240 (2400)
Расчетные сопротивления напрягаемой арматуры следует принимать по таблице 2.2. При наличии сведений о марке и классе арматурной стали, использованной в пролетном строении, допускается устанавливать ее расчетные сопротивления согласно указаниям СНиП 2.05.03-84. Расчетные сопротивления арматурной стали для ненапрягаемой арматуры Rsf при расчете элементов и напрягаемой арматуры Rpf при расчете элементов на выносливость следует определять по формулам:
где Таблица 2.2. Расчетные сопротивления напрягаемой арматуры
Таблица 2.3. Коэффициенты
Коэффициенты R 20,0 (200) 30,0 40,0 50,0 60,0 и менее (300) (400) (500) (600)
Для промежуточных значений прочности бетона коэффициент Модуль упругости ненапрягаемой арматуры Es принимают равным 2.3. Асимметрию цикла напряжений для бетона пролетных строений с ненапрягаемой арматурой следует определять по формуле
где Mp – изгибающий момент в расчетном сечении элемента от постоянных нагрузок; Mk – изгибающий момент в расчетном сечении элемента от временной нагрузки. Значения Mp определяют: для внутренней и внешней консолей плиты балластного корыта по формулам (4.8) и (4.9) при для монолитного участка плиты балластного корыта между соседними ребрами по формуле
для главной балки по формуле (4.22) при Значения Mk определяют: для плиты балластного корыта по формуле
для главной балки по формуле
В формулах (2.5) – (2.7): A – коэффициент, равный: для внешней и внутренней консолей плиты …………..0,5 для монолитного участка плиты между соседними ребрами: в сечении I 0,0625 в сечении II 0,1 pb, pp – нагрузки соответственно от веса плиты и веса балласта; lp – расстояние между внутренними гранями ребер;
la – длина распределения временной нагрузки: для внешней консоли плиты для внутренней консоли плиты для монолитного участка плиты
b – расчетная ширина плиты, принимаемая равной 1 м; l0 – длина распределения временной нагрузки, определяемая по формуле (4.4) или (4.5);
Асимметрию цикла напряжений для ненапрягаемой арматуры следует принимать: При » » Здесь
НАГРУЗКИ И КОЭФФИЦИЕНТЫ 3.1. Нормативные вертикальные нагрузки от веса пролетного строения и балласта с частями пути определяют по фактическим размерам элементов пролетного строения и балластной призмы с учетом удельных весов материалов Балласт щебеночный 17,0 (1,70) То же с частями верхнего строения пути 20,0 (2,00) Железобетон 25,0 (2,50) Бетон на гравии или щебне из природного камня 23,5 (2,35) Сталь 78,5 (7,85) Сосна, ель, кедр 7,0 (0,70) Дуб и лиственница 9,0 (0,90) При определении нагрузок, действующих на главную балку, вес балласта с частями пути учитывают в пределах плиты, относящейся к данной балке. Нагрузку на плиту пролетного строения от веса балласта с частями пути принимают равномерно распределенной на участке длиной 1 м в направлении вдоль оси моста. Для внешних консолей плиты интенсивность указанной нагрузки по направлению расчетного пролета (поперек оси моста) определяют с учетом конфигурации балластной призмы. 3.2. Распределение нагрузки от собственного веса элементов пролетного строения разрешается принимать равномерным по длине пролета, если действительная нагрузка на отдельных его участках отклоняется от средней не более чем на 10%. 3.3. Коэффициент надежности по нагрузке np для всех постоянных нагрузок, кроме веса балласта с частями пути, принимают равным 1,1. Коэффициент надежности по нагрузке 3.4. Динамические коэффициенты к эталонной нагрузке а) при расчете главной балки для эталонной нагрузки и для всех поездных нагрузок в зависимости от толщины балластного слоя под шпалой h0 по оси моста: при
при
где l – расчетный пролет, м; для промежуточных значений hb значения для консольных кранов в рабочем положении
б) при расчете плиты балластного корыта hb, м. 0,25 0,50 0,75 1,00
для промежуточных значений hb значения Уменьшение динамической добавки 3.5. Коэффициент надежности по нагрузке nk для временной нагрузки принимают равным 1,15 независимо от длины загружения.
Рис. 3.1. Зависимость динамического коэффициента
3.6. Коэффициент при расчете главных балок (рис. 3.2)
где l – расчетный пролет, м. При расчете плиты балластного корыта
Рис. 3.2. Зависимость коэффициента
3.7. Долю временной нагрузки, приходящуюся на главную балку монолитного пролетного строения, расположенного на прямом участке пути, следует определять по формулам: а) для пролетных строений, имеющих две главные балки под один путь (рис. 3.3):
где A1, A2, B1, B2 – коэффициенты, принимаемые по табл. 3.1 (для балки 2 коэффициенты подставляют в формулы (3.3) и (3.4) с обратным знаком);
Рис. 3.3. Схема расположения пути на пролетном строении
Таблица 3.1. Коэффициенты A1, A2, B1 и B2
Примечание. Для промежуточных значений x коэффициент A2 определяют по интерполяции.
б) для пролетных строений, имеющих более двух главных балок под один путь,
где m – число балок; 3.8. Долю временной нагрузки, приходящуюся на главную балку сборного пролетного строения, расположенного на прямом участке пути, следует определять: а) для пролетных строений, имеющих две не связанные между собой главные балки под один путь, по формулам (см. рис. 3.3):
Таблица 3.2. Доли временной нагрузки
Примечания. 1. Значение при x<0,5l
при x>0,5l
Знак «+» для балки 1, знак «-» для балки 2;
б) для пролетных строений, имеющих более двух не связанных между собой главных балок под один путь, 3.9. Долю временной нагрузки, приходящуюся на балку монолитного пролетного строения с ненапрягаемой арматурой, расположенного на кривой и имеющего две главные балки под один путь, следует определять по приложению 5. Если полученные при этом классы главных балок ниже соответствующих классов нагрузки, рекомендуется уточнить величины
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 263; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.210.35 (0.01 с.) |

 , (2.1)
, (2.1) - коэффициент, зависящий от асимметрии цикла напряжений
- коэффициент, зависящий от асимметрии цикла напряжений  (см. п. 2.3):
(см. п. 2.3): при фактической прочности бетона R в конструкции имеют следующие значения:
при фактической прочности бетона R в конструкции имеют следующие значения: Мпа (кгс/) (270) (295) (335) (360) (385)
Мпа (кгс/) (270) (295) (335) (360) (385) ; (2.2)
; (2.2) , (2.3)
, (2.3) ,
,  - коэффициенты, зависящие от асимметрии цикла напряжений в арматуре
- коэффициенты, зависящие от асимметрии цикла напряжений в арматуре  (см. п. 2.3) и принимаемые по табл. 2.3.
(см. п. 2.3) и принимаемые по табл. 2.3. (условное отношение модулей упругости арматуры и бетона), используемые в расчетах элементов с ненапрягаемой арматурой на выносливость, принимают в зависимости от фактической прочности бетона R в конструкции, МПа (кгс/см2):
(условное отношение модулей упругости арматуры и бетона), используемые в расчетах элементов с ненапрягаемой арматурой на выносливость, принимают в зависимости от фактической прочности бетона R в конструкции, МПа (кгс/см2): МПа (
МПа ( кгс/см2), напрягаемой арматуры Ep -
кгс/см2), напрягаемой арматуры Ep -  МПа (
МПа ( кгс/см2).
кгс/см2). , (2.4)
, (2.4) ;
; ; (2.5)
; (2.5) ; (2.6)
; (2.6) . (2.7)
. (2.7) - минимальное значение допускаемой временной нагрузки k, полученное при расчете на прочность соответственно плиты балластного корыта или главных балок;
- минимальное значение допускаемой временной нагрузки k, полученное при расчете на прочность соответственно плиты балластного корыта или главных балок; ;
; ;
; ;
; - коэффициент, принимаемый по табл. 4.1;
- коэффициент, принимаемый по табл. 4.1; - коэффициент уменьшения динамического воздействия временной нагрузки, принимаемый по приложению 4;
- коэффициент уменьшения динамического воздействия временной нагрузки, принимаемый по приложению 4; - площадь линии влияния изгибающего момента, определяемая по формуле (4.21);
- площадь линии влияния изгибающего момента, определяемая по формуле (4.21);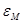 - доля временной нагрузки, приходящаяся на главную балку (см. пп. 3.7 – 3.9).
- доля временной нагрузки, приходящаяся на главную балку (см. пп. 3.7 – 3.9).





 , кН/м3 (тс/м3):
, кН/м3 (тс/м3): для веса балласта с частями пути принимают равным 1,2.
для веса балласта с частями пути принимают равным 1,2. и к нагрузке от обращающегося подвижного состава
и к нагрузке от обращающегося подвижного состава  принимают равными:
принимают равными: м
м ; (3.1)
; (3.1) м
м
 ;
; 1,50 1,43 1,33 1,27
1,50 1,43 1,33 1,27 в расчетах на выносливость учитывают с помощью коэффициента
в расчетах на выносливость учитывают с помощью коэффициента 
 от минимального расстояния между осями ak в схеме временной нагрузки
от минимального расстояния между осями ak в схеме временной нагрузки , предназначенный для унификации результатов классификации главных балок металлических и железобетонных мостов, принимают:
, предназначенный для унификации результатов классификации главных балок металлических и железобетонных мостов, принимают: , (3.2)
, (3.2) .
.
 ; (3.3)
; (3.3) , (3.4)
, (3.4)




 - смещение оси пути, м, относительно оси пролетного строения соответственно над левым (x=0) и правым (x=l) опорными сечениями; величины
- смещение оси пути, м, относительно оси пролетного строения соответственно над левым (x=0) и правым (x=l) опорными сечениями; величины  ,
,  (3.5)
(3.5) - смещение оси пути относительно оси пролетного строения, определяемое для
- смещение оси пути относительно оси пролетного строения, определяемое для  по формуле
по формуле  ;
;  - над соответствующим опорным сечением;
- над соответствующим опорным сечением; 
 - расстояния от оси соответственно i -й и j -й балок до оси пролетного строения с учетом знака.
- расстояния от оси соответственно i -й и j -й балок до оси пролетного строения с учетом знака. ; (3.6)
; (3.6) ; (3.7)
; (3.7) . (3.8)
. (3.8) по табл. 3.2.
по табл. 3.2. на основании результатов испытания пролетного строения (см. п. 8.10).
на основании результатов испытания пролетного строения (см. п. 8.10).


