
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Влияние нормы сбережений на экономический рост в рамках модели Солоу.
43. Золотой уровень накопления капитала в экономике, k** (на примере производственной функции Кобба-Дугласа). Планируя экономическую политику, правительство ставит цель максимизации экономического благосостояния общества, т.е. максимизация потребления. Возникает вопрос, при каком уровне капиталовооруженности достигается максимум потребления. Математически данная задача ставится:
Решение этой задачи позволяет определить норму сбережения, обеспечивающую наивысшее потребления в устойчивом состоянии экономики. Уровень накопления капитала, обеспечивающий устойчивое состояние с максимальным потреблением, называется золотым уровнем накопления капитала k**.
Золотое правило накопления реализуется в случае, если каждое поколение сберегает для будущих поколений такую же часть национального дохода, какую ему оставляет предыдущее поколение. Для определения золотой нормы сбережения мы имеем два условия:
Из этого следует, что золотая норма сбережений находится:
44. Модель Солоу динамики запаса основного капитала в экономике с учетом роста населения. Устойчивый уровень капиталовооруженности живого труда (на примере функции Кобба-Дугласа) и динамика ВВП. Изменение затрат труда в экономике может быть описано с помощью соотношения:
Непрерывным аналогом этого соотношения является дифференциальное уравнение:
Решение имеет вид:
С учетом фактора труд изменение запаса капитала в экономике в расчете на одного работника составляет:
Это уравнение показывает, что рост населения уменьшает капиталовооруженность таким же образом, как и выбытие капитала. Рост население уменьшает
Влияние темпа прироста населения на экономический рост в рамках модели Солоу. Изменение затрат труда в экономике может быть описано с помощью соотношения:
Непрерывным аналогом этого соотношения является дифференциальное уравнение:
Решение имеет вид:
С учетом фактора труд изменение запаса капитала в экономике в расчете на одного работника составляет:
Это уравнение показывает, что рост населения уменьшает капиталовооруженность таким же образом, как и выбытие капитала. Рост население уменьшает
46. Золотой уровень накопления капитала в экономике, k** с учетом роста населения (проиллюстрировать примером с функцией Кобба-Дугласа). Вернемся к тождеству национальных счетов в форме Солоу Уровень накопления капитала в экономике называется накоплением по «золотому» правилу, если величина Необходимое условие устойчивого состояния экономики на уровне «золотого» правила накопления капитала: Решением этого уравнения является
|
|||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 665; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.251.37 (0.005 с.) |
 - норма сбережений. Это переменная экзогенная.
- норма сбережений. Это переменная экзогенная.

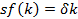



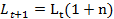 , где
, где  – темп прироста затрат труда.
– темп прироста затрат труда.
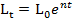 – это уравнение описывает динамику затрат живого труда в краткосрочном периоде.
– это уравнение описывает динамику затрат живого труда в краткосрочном периоде.
 , распределяя запас между большим числом занятых в экономике. Таким образом,
, распределяя запас между большим числом занятых в экономике. Таким образом, 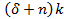 отражает критическую величину инвестиций, т.е. величину, необходимую для поддержания достигнутой капиталовооруженности.
отражает критическую величину инвестиций, т.е. величину, необходимую для поддержания достигнутой капиталовооруженности. и предположим, что национальная экономика находится в устойчивом состоянии; пометим основное тождество в данной ситуации следующим образом:
и предположим, что национальная экономика находится в устойчивом состоянии; пометим основное тождество в данной ситуации следующим образом:  . Вспомним, что в устойчивом состоянии
. Вспомним, что в устойчивом состоянии  определяется как
определяется как  , и заменим
, и заменим  на
на  , тогда тождество перепишется в виде
, тогда тождество перепишется в виде  . Получается, что в устойчивом состоянии потребление на единицу труда с постоянной эффективностью является функцией аргумента
. Получается, что в устойчивом состоянии потребление на единицу труда с постоянной эффективностью является функцией аргумента  , а
, а  зависит от
зависит от  .
. .
.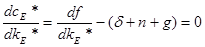
 - золотое правило накопления капитала. => MPK=(
- золотое правило накопления капитала. => MPK=( +n+g).
+n+g). Дадим геометрическую интерпретацию
Дадим геометрическую интерпретацию


