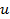Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Безразличные наборы благ и отношение безразличия на пространстве благ (rin). Свойства множеств безразличия.
Наборы будем называть безразличными потребителю, если одновременно справедливы след. рав-ва:
Безразличные наборы благ будем обозначать (1). Множеством безразличия к элементу
Моделью способности потребителя идентифицировать безразличные наборы благ служит функция (2):
(2) - это функция отношения безразличия. Для каждой пары элементов потребитель способен высказать одну из двух альтернатив: 1)наборы безразличны друг другу; 2) наборы небезразличны друг другу. К свойствам множеств безразличия можно отнести следующую теорему: 1. 2. Замечание: для одномерного пространства благ множество безразличия состоит из одного этого элемента.
6. Теорема Дебре о функции полезности. Свойства функции полезности: возрастание по каждому аргументу и закон Госсена (на примере логарифма Бернулли).
Теорема Дебре: если отношение предпочтения потребителя (rwp) транзитивно, непрерывно и удовлетворяет аксиоме ненасыщаемости, то существует непрерывная на пространстве благ С скалярная функция(обозначим ее U), которая возрастает по каждому аргументу, такая что, rwp ( Свойства функции полезности: 1)Непрерывность 2)Дифференцируемость 3)Убывание предельной полезности 4)Возрастает по каждому аргументу 5)Выпукла вверх Конкретно рассмотрим свойство 4. Возрастание потребления одного при неизменном потреблении другого продукта ведет к росту потребительской оценки (возрастанию функции полезности).
Первые частные производные называются предельными полезностями продуктов.
Теперь обратимся к свойству 3. Предельная полезность каждого продукта уменьшается, если объем его потребления продолжает расти при неизменном потреблении остальных. Это свойство называется законом убывания предельной полезности (закон Госсена). Это следует из аксиомы выпуклости.
Можно сказать, что функция полезности строго вогнута, то есть полезность любого товар уменьшается по мере его потребления.
Рассмотреть на логарифме Бернулли. u=a1*ln(x1-c1)+…+an*ln(xn-cn) xi>ci,ci≥0, ai≥0
7. Теорема Дебре о функции полезности. Свойства функции полезности: выпуклость вверх (на примере неоклассической функции полезности). Теорема Дебре: если отношение предпочтения потребителя (rwp) транзитивно, непрерывно и удовлетворяет аксиоме ненасыщаемости, то существует непрерывная на пространстве благ С скалярная функция(обозначим ее U), которая возрастает по каждому аргументу, такая что, rwp ( Функция полезности является дважды дифференцируемой и имеет непрерывные частные производные. Ее матрица Гессе, состоящая из вторых производных, отрицательно определена. Это означает, что функция полезности строго вогнута.
8. Теорема Дебре о функции полезности. Свойства функции полезности: кривые безразличия и предельные нормы замещения благ (на примере неоклассической функции полезности).
Теорема Дебре: если отношение предпочтения потребителя (rwp) транзитивно, непрерывно и удовлетворяет аксиоме ненасыщаемости, то существует непрерывная на пространстве благ С скалярная функция(обозначим ее U), которая возрастает по каждому аргументу, такая что, rwp (
Множество линий безразличия называется карта линий безразличия. Каждая кривая представляет собой наборы потребительских товаров и услуг, которые человек оценивает одинаково. Свойства функции полезности означают, что линия безразличия убывает и строго выпукла к началу координат.
Количество денежных средств, которыми располагает потребитель, ограничено, поэтому он должен искать компромисс, когда делает выбор между товарами, и кривые безразличия могут помочь. Перемещаясь вдоль кривой безразличия сверху вниз, видно, что потребитель котов отказаться от определенного количества единиц потребляемого товара
9. Модель Маршалла-Вальраса поведения потребителя и её трансформация к приведённой форме методом Лагранжа (на примере неоклассической функции полезности). Свойство спроса по Маршаллу-Вальрасу. Неоклассическая модель(модель Маршалла-Вальраса) поведения в структурной форме:
Смысл: потребитель выбирает такой набор благ, который максимально полезен, а также доступен по деньгам. Экзогенные переменные: C, Эндогенные переменные: Трансформируем ее к приведенной форме методом Лагранжа. 1) 2) Составим необходимые условия экстремума функции Лагранжа(найдем первые производные по каждой переменной и множителю Лагранжа) 3) Решим получившуюся систему уравнений Отметим свойство функции спроса: 1)Положительная однородность степени 0 относительно цен и дохода
10. Косвенная функция полезности и смысл множителя Лагранжа (на примере неоклассической функции полезности). Если подставить функцию спроса в качестве аргументов в функцию полезности, то в итоге она превратится в функцию экзогенных переменных.
Свойства: 1) Производная функции по М совпадает с множителем Лагранжа.
Множитель Лагранжа равен предельной полезности денег (дополнительного значения полезности спроса в ответ на дополнительную единицу денег). Другими словами, множитель Лагранжа показывает, на сколько изменится полезность потребителя, если его доход изменится на малую единицу. 2) 11. Косвенная функция полезности и тождество Роя (на примере неоклассической функции полезности). Если подставить функцию спроса в качестве аргументов в функцию полезности, то в итоге она превратится в функцию экзогенных переменных.
Свойства:
1) Производная функции по М совпадает с множителем Лагранжа.
2) В левой части размещается предельная полезность спроса потребителя по цене блага (изменение единицы спроса в ответ на изменение дополнительной единицы блага). 3)функция, не возрастающая по цене. 4)функция, не убывающая по доходу. 5)функция однородная нулевой степени 6)функция является квазивыпуклой по цене. 7)функция непрерывна на всех р>0, M>0
12. Модель Хикса поведения потребителя и её трансформация к приведённой форме методом Лагранжа (на примере неоклассической функции полезности). Свойство спроса по Хиксу. Модель Хикса является альтернативой модели Маршалла-Вальрасса и описывается следующими утверждениями. Потребитель на рынке стремится выбрать такой набор благ, чтобы с одной стороны этот набор доставил потребителю заданный уровень полезности (удовлетворение), а с другой стороны минимизировать затраты от посещения рынка.
Экзогенные переменные: р-цены, Эндогенные переменные: М-доход, Трансформируем модель методом Лагранжа к виду:
Свойство:
13. Функция расходов потребителя и её свойства (на примере неоклассической функции полезности). Подставим уровень расходов потребителя в целевую функцию как аргумент
Свойства: 1)функция является не возрастающей по цене 2)функция является однородной первой степени по ценам
3)является вогнутой по цене 4)функция непрерывная в пространстве цен 5)функция возрастает по 14. Лемма Шепарда и тип благ в спросе по Хиксу (на примере неоклассической функции полезности). Лемма Шепарда: для функции расходов М и функции спроса по Хиксу справедливо следующее соотношение:
Получается, что предельные расходы потребителя по ценам благ равны спросу по Хиксу этих благ.
Классификация благ в спросе потребителя. Если с ростом цен спрос на товар снижается, то товар называется нормальным; если спрос повышается, то такие товары называются товарами Гиффина. 1) нормальное благо 2) гиффиново (аномальное) благо
Если с ростом дохода спрос на товар повышается, то такой товар называется ценным, если наоборот, то малоценным. 1) ценное благо 2) малоценное благо
15. Матрица Слуцкого и экономический смысл её элементов (на примере неоклассической функции полезности).
Трактовка матрицы Слуцкого: - столбец номер j этой матрицы имеет смысл изменения спроса потребителя при сохранение уровня полезности в ответ на увеличение i блага на единицу.
|
|||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 286; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.234.191 (0.033 с.) |

 (1)
(1) называется множество безразличных элементу
называется множество безразличных элементу 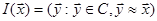

 , то
, то  Ø (множества безразличия небезразличных наборов благ не пересекаются в пространстве благ);
Ø (множества безразличия небезразличных наборов благ не пересекаются в пространстве благ); Пространство благ – объединение всех множеств безразличия.
Пространство благ – объединение всех множеств безразличия. =A то u(
=A то u(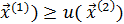 . Если наборы благ безразличны, то неравенство превращается в равенство.
. Если наборы благ безразличны, то неравенство превращается в равенство.
 .
.



 Линия, соединяющая потребительские наборы (
Линия, соединяющая потребительские наборы ( ), имеющие один и тот же уровень удовлетворения потребностей потребителя, называется линией безразличия. Это есть линии уровня функции полезности.
), имеющие один и тот же уровень удовлетворения потребностей потребителя, называется линией безразличия. Это есть линии уровня функции полезности. Лемма: кривые безразличия не могут пересекаться.
Лемма: кривые безразличия не могут пересекаться. в пользу товара
в пользу товара  . Чтобы количественно определить, каким объемом того или иного товара потребитель готов пожертвовать ради увеличения потребления другого товара, используется предельная норма замещения.
. Чтобы количественно определить, каким объемом того или иного товара потребитель готов пожертвовать ради увеличения потребления другого товара, используется предельная норма замещения. – норма замещения первого продукта вторым на потребительском наборе (
– норма замещения первого продукта вторым на потребительском наборе ( – предельная норма замещения первого продукта вторым.
– предельная норма замещения первого продукта вторым.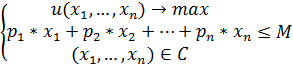
 (функция полезности), M – доход потребителя, p – цены.
(функция полезности), M – доход потребителя, p – цены.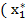 ,
,  ,
, 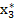 ,…,
,…,  ) – наилучший набор
) – наилучший набор
 Это означает, что при одновременном изменении цен и доходов в одинаковое число раз, спрос не меняется.
Это означает, что при одновременном изменении цен и доходов в одинаковое число раз, спрос не меняется.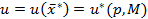

 - тождество Роя
- тождество Роя
 -полезность,
-полезность,  ,
, 
 Если цены изменяются в m раз, то спрос не изменяется.
Если цены изменяются в m раз, то спрос не изменяется. . В итоге затраты на данный спрос будут выражены через экзогенные переменные.
. В итоге затраты на данный спрос будут выражены через экзогенные переменные.