
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод незатухающих колебанийСодержание книги
Поиск на нашем сайте
Этот метод позволяет определить настройки регулятора, обеспечивающие определенный запас устойчивости АСР и удовлетворительное качество переходных процессов. Определение настроек регулятора производиться в два этапа: определяется критическая частота определение по Кркр настроек регуляторов по приближенным формулам. Определение критической частоты Если разомкнутая система устойчивая и ее АФХ проходит через точку Условие нахождения АСР на границе устойчивости:
тогда получим:
это условие выполняется, если:
Амплитудно-фазовая характеристика пропорционального регулятора имеет вид:
или в показательной форме:
для расчета настройки Кркр и частоты
Из второго уравнения находим значение
Определение настроек регуляторов
По критическим значениям Кркр и
Пропорциональный (П) регулятор:
Пропорционально-дифференциальный (ПД) регулятор:
или
где,
Пропорционально-интегрально-дифференциальный (ПИД) регулятор:
где, Тпр – время предварения Тпр=С2 /Кр
Вычисление настройки регуляторов, обеспечивают степень затухания процесса регулирования
На производстве достаточно часто находят настройки П,ПИ,ПИД – регуляторов по приближенным формулам, зависящем от некоторых характерных параметров динамики объекта: - времени запаздывания - постоянной времени Т0; - коэффициента усиления К0.
Пропорциональный (П) регулятор:
Пропорционально дифференциальный (ПД) регулятор:
Пропорционально-интегрально-дифференциальный (ПИД) регулятор:
Найденные настройки обеспечивают устойчивый переходной процесс со степенью затухания
Пример: Определить критическую частоту Поскольку АФХ П-регулятора имеет вид
Из второго уравнения находиться значение
Решая последнее уравнение, находим
Определяем настройки регуляторов. Расчет настроек регуляторов по П-регулятор
Расчет настроек по амплитудно-фазовой характеристики объекта
При использовании метода определения настройки регулятора по АФХ объекта необходимо обеспечить выполнение установленных требований к расположению характеристики на комплексной плоскости, обусловленных заданными значениями показателя колебательности М, запасов устойчивости по модулю С и фазе Настройка П-регулятора. Построить АФХ разомкнутой системы с регулятором при k1== 1, совпадающую с АФХ объекта, и провести луч под углом Вычертить окружность радиуса r с центром на вещественной отрицательной полуоси, касающуюся АФХ объекта и луча. Рассчитать максимальное значение коэффициента усиления П-регулятора по формуле:
Настройка И-регулятора. Построить АФХ разомкнутой системы для некоторого фиксированного значения, постоянной времени Т1 интегрального регулятора и k1 = 1 в выражении для его коэффициента усиления kа == k1/T1, что сведется к повороту по часовой стрелке на 90° векторов АФХ объекта, уменьшенных в T1 Провести луч под углом Рассчитать оптимальное предельное значение коэффициента усиления интегрального регулятора:
Рис.1.6. Рис.1.7.
Рис.1.8.
Настройка ПИ-регулятора. Построить АФХ разомкнутой системы для нескольких фиксированных значений Ти по выражению
при kp=1, что сведется к повороту на 90° в отрицательном направлении измененного в Провести луч под углом Определить значения коэффициентов усиления регулятора для каждого ТИ, так же, как и для П-регулятора, т. е. по формуле (1). Построить кривую границы области устойчивости (при заданном М) в плоскости параметров настройки ПИ-регулятора kp и ТИ (Рис.1.8.). Проведя касательную к этой кривой, можно выявить точку максимального отношения kp/TИ, являющегося оптимумом настройки.
Настройка ПИД-регулятора. Характеристики для различных значений ТИ, при единичном значении kp строится для фиксированного оптимального отношения времени предварения к времени изодрома Тп/Ти
При этом построение сведется к повороту на 90° в отрицательном направлении измененных в (1/ТИ
их с исходными векторами (Рис.1.9). Провести луч под углом Определить значения коэффициентов усиления регулятора для каждого ТИ, так же, как и для П-регулятора, т. е. по формуле (1). Построить кривую границы области устойчивости (при заданном М) в плоскости параметров настройки ПИ-регулятора kp и ТИ (Рис.1.8.). Проведя касательную к этой кривой, можно выявить точку максимального отношения kp/TИ, являющегося оптимумом настройки.
Рис.1.9.
Пример: Математически определяем объект регулирования, получается модель объекта, Рис.1.6. которая описывается апериодическим звеном первого порядка с передаточной функцией первого порядка:
р заменим на числитель и знаменатель умножаем на знаменатель сопряженный:
Выделяем действительную и мнимую часть, строим АФХ
Подставляя значения ( Проводим луч под углом
Вычерчиваем окружность радиуса r с центра на вещественной отрицательной полуоси, касающуюся АФХ разомкнутой системы и луча.
Рассчитываем максимальное значение коэффициента усиления ПИ-регулятора по формуле:
рис.1.10.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 405; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.72.229 (0.006 с.) |

 и критическая настройка Кркр пропорционального регулятора, при которой в замкнутой АСР возникают затухающие колебания у(t);
и критическая настройка Кркр пропорционального регулятора, при которой в замкнутой АСР возникают затухающие колебания у(t); , то замкнутая АСР будет находиться на границе устойчивости.
, то замкнутая АСР будет находиться на границе устойчивости.




 получим два уравнения:
получим два уравнения:

 определяем настройки регуляторов
определяем настройки регуляторов


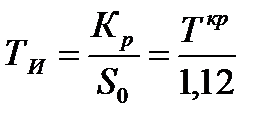
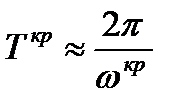 - период незатухающих колебаний АСР
- период незатухающих колебаний АСР
 ;
;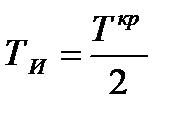
 ;
;
 более чем 0,75.
более чем 0,75. ;
;
 ;
; 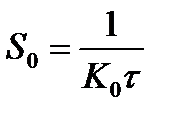
 ;
;  ;
; 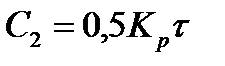
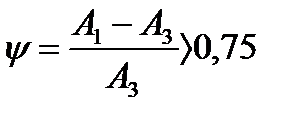
 и настройки
и настройки  . (Рис.1.1.).
. (Рис.1.1.).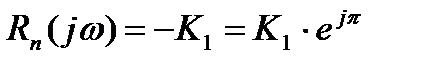 , то для расчета настройки
, то для расчета настройки  и частоты
и частоты  получим два уравнения:
получим два уравнения: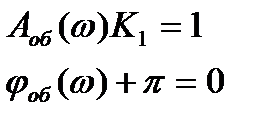

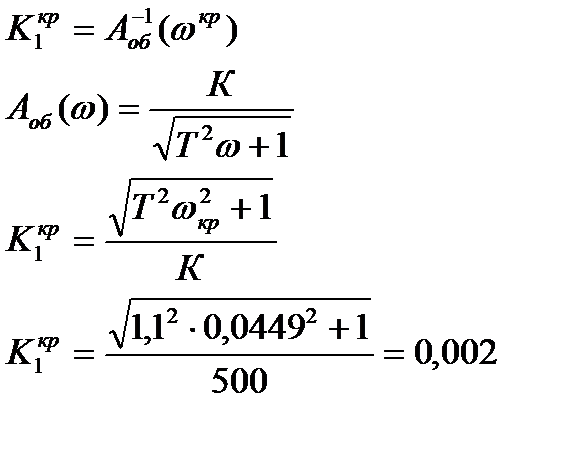
 и
и  осуществляется по приближенным формулам:
осуществляется по приближенным формулам: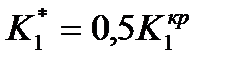

 р, времени регулирования tр. При отсутствии наперед заданных значений какого-либо из показателей качества следует принимать М = 1,3—1,5, что обеспечит хорошее качество переходных процессов в замкнутой системе регулирования.
р, времени регулирования tр. При отсутствии наперед заданных значений какого-либо из показателей качества следует принимать М = 1,3—1,5, что обеспечит хорошее качество переходных процессов в замкнутой системе регулирования. (1/М) к отрицательной полуоси (Рис.1.6.)
(1/М) к отрицательной полуоси (Рис.1.6.) (1)
(1) раз (Рис.1.7.)
раз (Рис.1.7.) и определить радиус r окружности, касающейся луча и построенной АФХ разомкнутой системы.
и определить радиус r окружности, касающейся луча и построенной АФХ разомкнутой системы. (2)
(2)


 ТИ раз вектора АФХ объекта и геометрическому суммированию его с исходным, как показано на (Рис1.8.).
ТИ раз вектора АФХ объекта и геометрическому суммированию его с исходным, как показано на (Рис1.8.). (1/М) и определить радиусы окружностей, касающихся этого луча и АФХ с фиксированными значениями ТИ.
(1/М) и определить радиусы окружностей, касающихся этого луча и АФХ с фиксированными значениями ТИ. 0,5. Выражение для АФХ системы представится в таком виде:
0,5. Выражение для АФХ системы представится в таком виде:
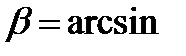 (1/М) и определить радиусы окружностей, касающихся этого луча и АФХ с фиксированными значениями ТИ.
(1/М) и определить радиусы окружностей, касающихся этого луча и АФХ с фиксированными значениями ТИ.
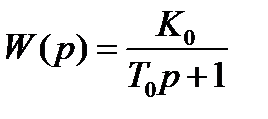
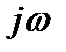


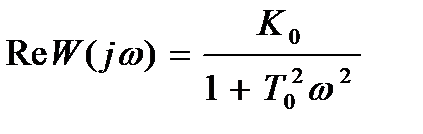 и
и 
 строим АФХ разомкнутой системы с К1=1 для фиксированных значений Тu (в нашем случае Тu=1,1). Для этого вектор АФХ замкнутой системы изменяем в Тu
строим АФХ разомкнутой системы с К1=1 для фиксированных значений Тu (в нашем случае Тu=1,1). Для этого вектор АФХ замкнутой системы изменяем в Тu  , где Х – длина вектора замкнутой АФХ) и геометрически суммируем его с исходным.
, где Х – длина вектора замкнутой АФХ) и геометрически суммируем его с исходным.
 отрицательной полуоси.
отрицательной полуоси.





