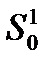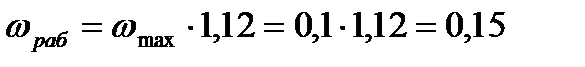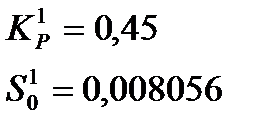Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод расширенных частотных характеристикСодержание книги
Поиск на нашем сайте
Обычная частотная характеристика отражает свойства исследуемого звена при подаче на вход синусоидальных возмущений с постоянной амплитудой.
или показательной форме:
где, BВХ – амплитуда синусоидальных колебаний;
Расширенная частотная характеристика отражает свойства объекта (или регулятора) при подаче на вход синусоидальных возмущений с затухающей амплитудой.
где, m – степень колебательности.
Степень колебательности процесса m – характеризует затухание его колебательных составляющих и численно равна абсолютному значению отношения действительной части к коэффициенту при мнимой части корня характеристического уравнения с наименьшим абсолютным значением этого отношения.
Между степенью затухания
Различным значениям степени затухания соответствуют следующие степени колебательности m.
Расширенные частотные характеристики W(m,j
Последовательность определения параметров настройки
Определяется расширенная частотная характеристика объекта
или в показательной форме
Определяется расширенная частотная характеристика пропорционально интегрального (ПИ) регулятора с передаточной функцией.
где, К0 – коэффициент усиления регулятора; S0=1/TИ, ТИ – время изодрома регулятора.
Знак минус указывает, что действие регулятора направлено против возмущения.
по показательной форме:
Исходным условием для получения заданной степени колебательности замкнутой системы m, а следовательно, определяемой степени затухания
Это соотношение двух комплексных чисел возможно в
том случае, если произведение модулей векторов равно единице, а аргументы (фазы) равны.
Тогда для АСР с ПИ – регулятором получается:
где,
Решая последние уравнения относительно Кр и S0, получают:
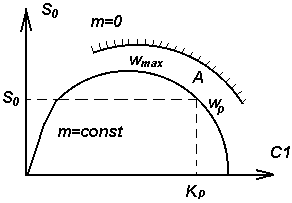
где, Задаваясь различными значениями частот Плоскость параметров настроек ПИ-регулятора.
Рис.1.4.
Формулы расчета настроек регулятора с пропорционально- дифференциальным (ПД), пропорциональным (П), пропорционально-интегрально-дифференциальным (ПИД) регуляторами имеют вид: Пропорциональный (П) регулятор:
Пропорционально-дифференциальный (ПИД) регулятор:
Пропорционально-интегрально-дифференциальный (ПИД) регулятор:
где,
Для построения семейства линии равной m, задается несколько значений В качестве оптимальных настроек выбираются настройки той САР, для которой критерий I2 окажется наименьшим. Пример: Определить оптимальные настроечные параметры ПИ-регулятора.
Исходные данные: Объект регулирования представлен передаточной функцией апериодического звена:
К0=571 см/м2; Т0=3657 с; m=0,221; Решение: Расширенная частотная характеристика объекта:
Заменим р на комплексную переменную
Подставляя численные значения К0, Т0 определяем Аоб
Определим фазо-частотную характеристику объекта
Определяем настройки регулятора
где,
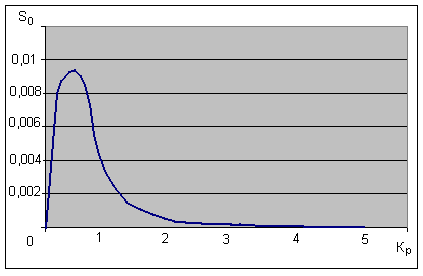
Вычисленные значения подставляем в выражения (1) и (2) составляем таблицу и строем кривую с равной m, по нему находим
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 1087; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.61.142 (0.008 с.) |


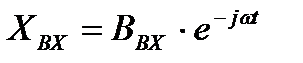
 - частота колебаний, рад/с.
- частота колебаний, рад/с.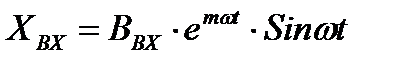
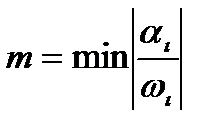 , i=1,2,3…;
, i=1,2,3…; 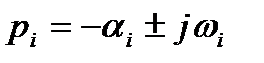
 и степенью колебательности m существует определенная связь.
и степенью колебательности m существует определенная связь.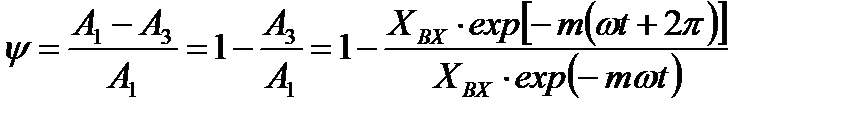
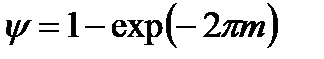
 ) получают аналитически из передаточных функций, заменой р на комплексную переменную
) получают аналитически из передаточных функций, заменой р на комплексную переменную 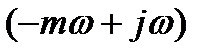 . При этом степень колебательности m обычно принимают равной 0,221 или 0,366, что соответствует степени затухания процесса
. При этом степень колебательности m обычно принимают равной 0,221 или 0,366, что соответствует степени затухания процесса 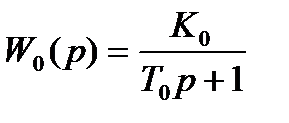 с передаточной функции
с передаточной функции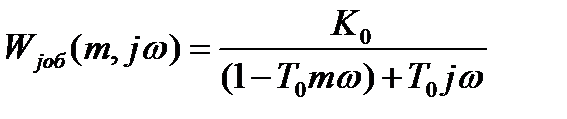
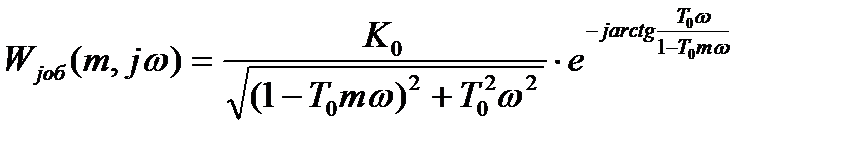

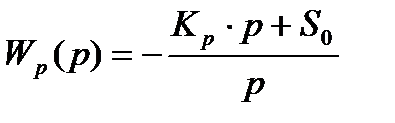
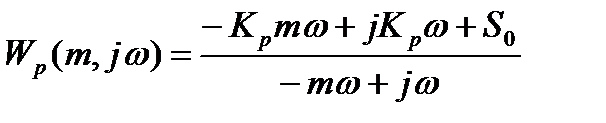
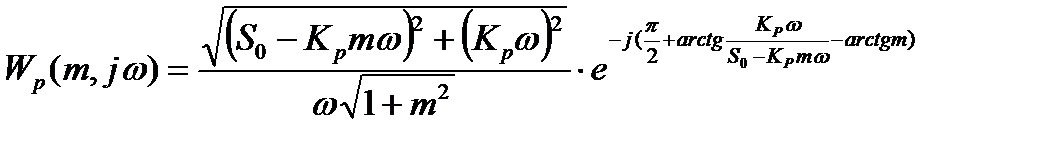
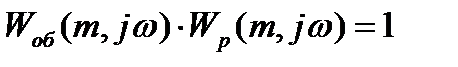
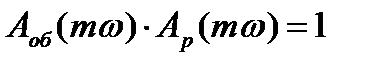
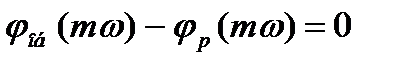

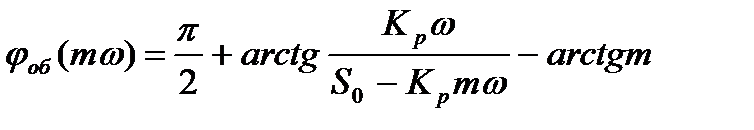
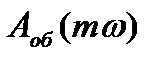 - расширенная амплитудно-частотная характеристика объекта;
- расширенная амплитудно-частотная характеристика объекта;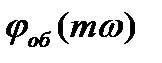 - расширенная фазо-частотная характеристика объекта;
- расширенная фазо-частотная характеристика объекта;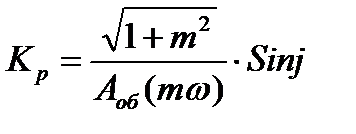
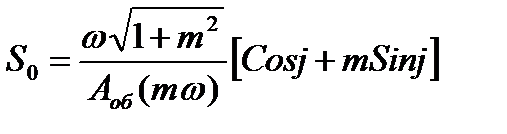
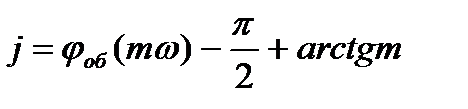
 max, а затем
max, а затем  р рабочую частоту и соответствующие ей оптимальные настройки
р рабочую частоту и соответствующие ей оптимальные настройки 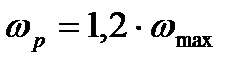
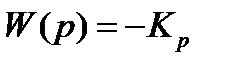
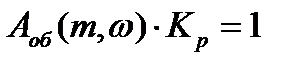
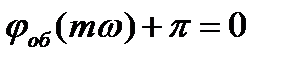
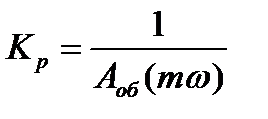
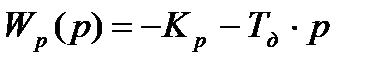

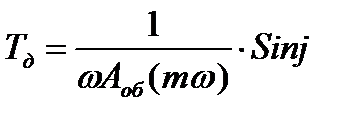
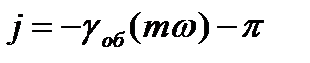
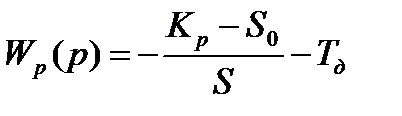
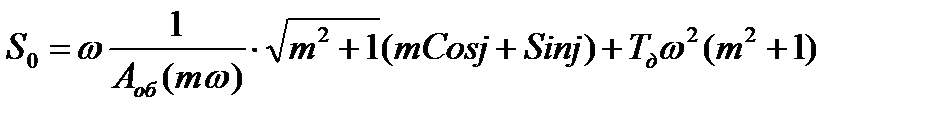
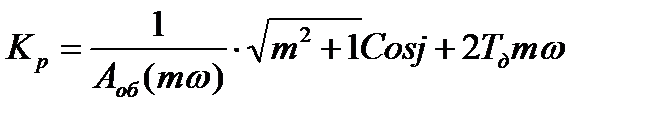
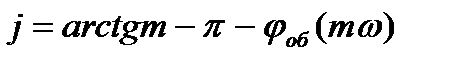
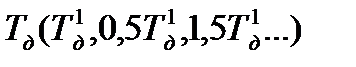 затем для каждого значения
затем для каждого значения 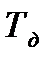 при различных значениях
при различных значениях 
 =0,75.
=0,75.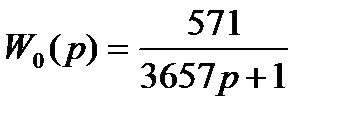
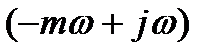 получаем расширенную амплитудно-фазовую характеристику.
получаем расширенную амплитудно-фазовую характеристику.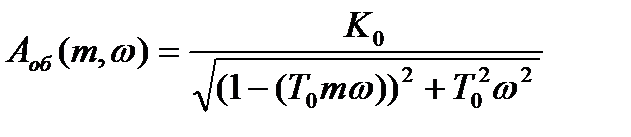
 при изменении
при изменении 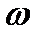 от 0 до
от 0 до 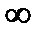 .
.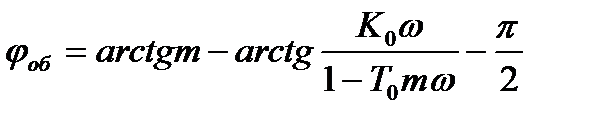
 об
об
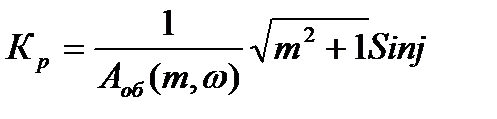 (1)
(1)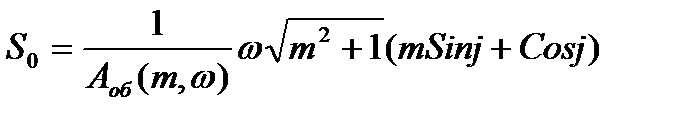 (2)
(2)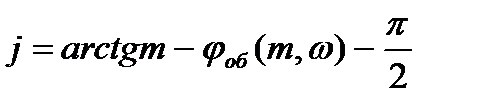
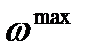 , а по соотношению
, а по соотношению 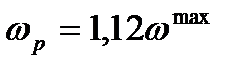 , рабочую частоту
, рабочую частоту 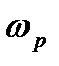 и соответствующую ей оптимальные настройки
и соответствующую ей оптимальные настройки 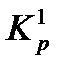 ,
,