
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основы теории конечных автоматов.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Алгоритм является фундаментальной контрацепцией информатики, и вопрос построения автоматических устройств, реализующих за данное алгоритмы, являются одним из сосновых вопросов проектирования микропроцессорных устройств отработки информации. Все существующие устройства обработки информации делятся на 2 большушие класса: 1) Функциональные преобразователи Эти устройства не учитывают входные сигналы, поступившие на вход в более ранние моменты времени, а реагируют только на входящие логические сигналы, эти устройства называются автоматами без памяти. 2) Автоматы, в которых результат преобразования информации, поступающей на вход, зависит не только от того, какая информация появилась на входе, но и от того, какая информация поступала на эти автоматы раньше. Такие устройства называются конечными автоматами или автоматами с памятью (примерами таких устройств являются биологические системы). На один и тот же входной сигнал конечный автомат (КА) может реагировать по-разному, в зависимости от того, в каком состоянии он находится в данный момент. При получении входного сигнала конечный автомат не только выдает информацию на выход, как функцию этого состояния, но и меняет свое состояние, поскольку входной сигнал меняет его предысторию. Число входных историй любого конечного автомата бесконечно, но счетно. Если автомат будет вести себя по-разному для каждой возможной предыстории, то он должен иметь бесконечный ресурс (память), чтобы все эти предыстории как-то фиксировать. Если ввести на множестве предысторий ---- то две предыстории можно считать эквивалентными, если они одинаковым образом влияют на дальнейшее поведение автомата. Очевидно, что для своего функционирования автоматам достаточно запоминать класс эквивалентности, к которому принадлежит предыстория. В случае, когда таких классов эквивалентности конечное число, является простейшим, но именно такая математическая модель представляет большую практическую ценность и получила широкое распространение. Соответствующая формальная модель и называется конечными автоматами. Математической модели конечного автомата внутреннее состояние автомата представляет собой класс эквивалентности предысторий. Упрощенно можно считать, что внутреннее состояние автомата это именно та его характеристика, которая однозначно определяет все последующие реакции автомата на внешнее событие.
Конечный автомат – это устройство, работающее в дискретные моменты времени (так называемые такты). В каждом таком такте на вход автомата подаются входные сигналы и на выходе появляется выходной сигнал и происходит изменение внутреннего состояния. Моменты срабатывания (такты) определяются либо специальными тактирующими сигналами, либо наступлением внешнего события, которое заключается в том, что на вход автомата приходит новый входной сигнал. В этом случае считается, что автомат управляется событиями и такты работы автомата имеют различную длительность в зависимости от прихода внешних сигналов.
Основные понятия и определения конечных автоматов
Конечным автоматом (автоматом Милли) называется математическая модель, состоящая из 5 элементов: (S,X,Y, δ, λ), где: S - конечное множество состояний {sl,s2,...Sk}; X - конечный входной алфавит; Y - конечный выходной алфавит; δ: S x X -> S - функция следующего состояния, отображающая текущее состояние и текущий вход в следующее состояние; λ: S х X -> Y - функция выхода, отображающая текущее состояние и текущий вход в выходной символ.
Если в конечном автомате выделено специальное начальное состояние S0, то этот автомат называется инициальным.
Два конечных автомата А1 и А2 эквивалентны, если реализуемые ими отображения вход-выход – эквивалентны. Две логические функции f1 и f2 эквивалентны, если на всех наборах аргументов они имеют одинаковые значения, т.к. число аргументов логической функции конечно, то достаточно сравнить значение этих функций на всех наборах аргументов. Конечный автомат реализует бесконечное множество входных последовательностей сигналов в конечное множество выходных сигналов, поэтому автоматные отображения вход->выход, нельзя определить простым перечислением их отображений и сравнить их значения на всех бесконечных множествах. Для того, чтобы определить эквивалентность автоматов необходимо расширить функции так, чтобы функции переходов и выходов были определены на множествах последовательностей сигналов входного алфавита (последовательных цепочках) элементов х.
Определение 2.3 Пусть A=<S, X, Y, S0 , d, l> - конечный автомат. Расширенными функциями перехода и выхода автомата А называются функции d*: S x X* ® S и l*: S x X*® Y*, определенные так: d*(S, e) = S; d*(Si,aaj)=d(d*(Si,a),aj)); ( 2-1) l*(S, e)= e; l*(Si,aaj)= l*(d*(Si,a),aj); (2-2) (e - пустая цепочка, альфа – сама цепочка Т.о. расширенные функции переходов и выходов определены на множестве входных последовательностей (входных цепочках) в отличие от обычных функций переходов и выходов, которые определены на множестве входных сигналов. Другими словами, для данного автомата А и его функций d А и l А могут быть определены не только на множестве X всех его входных букв, но и на множестве X* всех входных слов. Для любого входного слова a=aj1aj2...ajk d*(Si, aj1aj2...ajk) = d(d(...d(Si,aj1),aj2),...ajk-1)ajk Это традиционное определение с многоточиями, намного точнее и лучше читается, чем индуктивное определение.
Функция переходов задается: а) d(Si,aj) задается автоматной таблицей; б) для любого слова aÎX* и любой буквы aj d*(Si, aaj) = d(d*(Si,a), aj) (2-3) С помощью расширенной функции δ λ Зафиксируем в автомате А начальное состояние S ω=λ(S где Ù- операция конкатенации. Это соответствие, отображающее входные слова в выходные слова, называется автоматным отображением, а также автоматным (или ограниченно детерминированным) оператором. Если результатом применения автоматного оператора к входному слову α является выходное слово ω, то это будем обозначать соответственно A(S Автоматное отображение обладает двумя свойствами, которые непосредственно следуют из (2-5): слова a и w имеют одинаковую длину (свойство сохранения длины) и, кроме того, автоматные операторы – это операторы без предвосхищения, т.е. операторы, которые, перерабатывая слово слева направо, не заглядывают вперед. Это свойство отражает тот факт, что i-тая буква выходного слова зависит только от первых i букв входного слова. Определение 2.4 Пусть А=<S,X,Y,S Определение 2.5 Автомат А называется сильно связным, если из любого его состояния достижимо любое другое состояние. Определение 2.6 Автомат называется автономным, если его входной алфавит состоит из одной буквы X={a}. Определение 2.7 Автомат называется частичным или не полностью определенным, если хотя бы одна из двух функций не полностью определена. В таком автомате для некоторых пар (состояние – вход, состояние – выход) значения функций δ или λ не определены. В автоматной таблице неполная определенность автомата выражается в том, что некоторые её клетки не заполнены. Определение 2.8 Конечные автоматы А=<S
а) их входные алфавиты совпадают X б) реализуемые ими отображения совпадают: ( Однако ответить на вопрос, эквивалентны ли автоматы, перебором их реакций на все входные цепочки невозможно, т.к. их бесконечно много, поэтому проблема эквивалентности КА не является тривиальной. Метод решения этой задачи основан на понятии прямого произведения автоматов. Определение 2.9 Прямым произведением конечных автоматов А=<S AxB=<S а) ( б) (
14.Способы задания конечных автоматов. Устройство, оперирующие с логическими сигналами, принимающее только 2 значения – 0 и 1и имеющее некоторое множество внутренних эквивалентных состояний S, множество входных сигналом x и множество выходных сигналов y – называется цифровым автоматом. Простейшим цифровым автоматом является любое комбинационное устройство, имеющее единственное внутреннее состояние. В этом устройстве каждому набору входных логических переменных соответствует некоторый выходной сигнал. Если автомат может находится в нескольких эквивалентных внутренних состояниях, то его реакция на входные сигналы определяется не только текущим набором входных сигналов, но и внутренним состоянием автомата. Предполагается, что изменения входных сигналов и внутренних состояний происходит мгновенно, поэтому автомат работает в дискретном времени Ti, где протяженность каждого такта (интервала) может быть сколь угодно большой. Если в течении времени не произошло изменений входных сигналов x и соответственно внутренних состояний S. Различают автоматы Мура и автоматы Милли. Автомат Мура является частным случаем более широкого понятия – автомата Мили.
Автоматы Мура описываются следующими функциями переходов и выходов: Si+1 = f(Si, xi+1) yi+1 = f(Si+1) Каждое новое состояние автомата Мура обусловлено предшествующим состоянием и входным сигналом, а выходная функция – в каждый данный момент времени однозначно определяется состоянием автомата. Автоматы Мили отличаются от автоматов Мура тем, что выходной сигнал в этом автомате зависит не только от состояния, но и от входного сигнала. Si+1 = f(Si, xi+1) yi+1 = y(si, xi+1) Понятие внутреннего состояния автомата предполагает наличие у автомата внутренней памяти. Число различных эквивалентных состояний зависит от глубины памяти. В качестве элементов памяти могут использоваться стандартные модули ПЗУ или логические схемы с обратными связями в частности – различные типы триггеров. В принципе любой автомат Мура можно свести к автомату Мили и наоборот. Автомат Мили – более универсальное устройство У автомата Мили нет таких ограничений, которые есть у Мура Задав множество (x s y) достаточно трудно определить как работает конечный автомат. Приведенные выше уравнения, описывающие функционирование автоматов мура и мили устанавливают связь между множествами x s y, но они неудобны для описания функционирования конкретных автоматов, поэтому на практике получили распространение другие способы описания работы конечных автоматов. Наиболее широко распространены табличное задание, где заданы таблицы переходов и выходов конечного автомата. Здание конечного в виде граф-схемы, а так же задание конечных автоматов в виде ЛГСА (логическая схема алгоритмов). Рассмотрим задание КА, который для любой пары чисел, записанных в двоичной системе счисления вычисляет и выводит их сумму, при этом данные начинаются с битов, имеющие наименьшие разряды и числа читаются справа-налево. (в билетах будет пример с триггерами, RS и другие)
Таблица 2.1
Таблица выходной функции 2.2
В таблице 2.1 возможные состояния в виде упорядоченной последовательности записаны в 1ой строке. Входные сигналы в упорядоченном виде записаны в первом столбце. На пересечении строк и столбцов получаем клетку в которой записано новое состояние. Таблица переходов (2.1) может быть определена неполностью. В этом случае в таблице имеются прочерки в отдельных клетках. Некоторые сигналы не вызывают изменения состояния. Так, под действием входных сигналов 0 и 1автомат сохраняет состояние S0, Если он в нем находился и состояние S1, если при подаче такой комбинации входных сигналов он находился в состоянии S1. Множество выходных сигналов подобным образом задается для каждой пары Si, Lj и на пересечении соответствтвующей строки и столбца получаем выходной сигнал автомата. Значения выходного сиг Иногда, если имеется такая возможность – обе таблицы совмещают. Для автомата Мура таблица выходов вырождается в одну строку, которую можно записать в первой строке таблицы переходов.
Табличное описание служит удобным формализованным языком, на котором можно задать любой конечный автомат, что дает взаимопонимание между заказчиком и разработчиком. Распространенное средство описания автомата – логическая граф-схема описания алгоритма.
15. Конечный автомат как модель «реагирующей системы».
Последнее время для программистов, работающих в области информатики, стала ясна необходимость выделения особого класса систем, который был назван реагирующими системами. Эти системы способны реагировать на поток внешних событий. Оказалось, что математическая модель конечного автомата является удобным средством описания таких систем. Удобство применения математической модели конечного автомата состоит в том, что эта модель обладает ясностью семантики, наглядностью и выразительностью и в то же время она достаточно строга и формальна. Однако оказалось, что классическая математическая модель конечного автомата имеет ряд недостатков. Главным недостатком такой модели является отсутствие средств выражения иерархии состояния, а также математического аппарата для отображения прерываний и продолжения нормальной работы системы после обработки прерывания. Простым и достаточно эффективным расширением модели классического конечного автомата является введение понятия «внешнее событие», наступление которого можно считать условием перехода автомата в новое состояние. Такими событиями можно считать получение сигнала на вход автомата, прерывание и срабатывание таймера. Со срабатыванием таймера естественно связывается понятие времени в автомате. Действительно, введением понятия времени в конечном автомате можно связать с ограничением пребывания автомата в заранее заданном, конкретном состоянии. Такое ограничение, если оно необходимо, лучше всего задавать таймером математической модели конечного автомата, срабатывание таймера должно вызывать переход автомата в другое состояние. Рассмотрим в качестве примера спецификацию процесса, определяющего одинарный или двойной щелчок мыши. Напомним, что двойным щелчком считается последовательность из 2-х нажатий клавиши, разделяемая промежутком времени t=250мс. Представим граф переходов конечного автомата, решающего эту задачу.
16. Конечный автомат как модель протокола передачи сообщений в сетях.
|
|||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 1850; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.205.161 (0.012 с.) |

 определяется (также индуктивно) расширенная функция λ
определяется (также индуктивно) расширенная функция λ  , αa
, αa  )= λ(δ*(S
)= λ(δ*(S  и каждому слову α=aj
и каждому слову α=aj  ...a
...a  поставим в соответствие слово ω выходном алфавите У:
поставим в соответствие слово ω выходном алфавите У: )Ùλ(S
)Ùλ(S  ,δ,α>- конечный автомат. Состояние S
,δ,α>- конечный автомат. Состояние S  α∈X
α∈X  (
(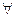 α∈X
α∈X  S
S 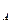 ,X
,X  , X
, X  (S
(S  > с одинаковым входным алфавитом X (обозначается AxB) называется автомат:
> с одинаковым входным алфавитом X (обозначается AxB) называется автомат: , λ
, λ  Иными словами, конечный автомат, являющийся прямым произведением двух КА, в качестве своих состояний имеет пары состояний, исходных автоматов, его начальное состояние есть пара их начальных состояний, выходной алфавит – множество пар выходных символов автоматов – множителей, а функции переходов и выходов определены покомпонентно. Т.о. прямое произведение КА – это просто два стоящих рядом невзаимодействующих КА, синхронно работающих на одном общем входе
Иными словами, конечный автомат, являющийся прямым произведением двух КА, в качестве своих состояний имеет пары состояний, исходных автоматов, его начальное состояние есть пара их начальных состояний, выходной алфавит – множество пар выходных символов автоматов – множителей, а функции переходов и выходов определены покомпонентно. Т.о. прямое произведение КА – это просто два стоящих рядом невзаимодействующих КА, синхронно работающих на одном общем входе
 нала автомата приведено в таблице 2.2
нала автомата приведено в таблице 2.2 По первому щелчку мыши (клик) автомат переходит из состояния S0 в состояние S1, и если до истечения следующих t=250мс на вход поступает еще один сигнал (событие клик), то на выход будет выдан сигнал click\double в противном случае t\click. В любом из этих вариантов автомат возвращается в положение S0 и работа автомата повторяется.
По первому щелчку мыши (клик) автомат переходит из состояния S0 в состояние S1, и если до истечения следующих t=250мс на вход поступает еще один сигнал (событие клик), то на выход будет выдан сигнал click\double в противном случае t\click. В любом из этих вариантов автомат возвращается в положение S0 и работа автомата повторяется.


