
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Протокол PAR передачи сообщений в сетяхСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
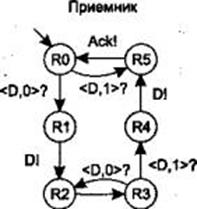
В качестве более сложного примера с использованием конечного автомата рассмотрим спецификацию протокола передачи информации в компьютерных сетях. Термин «протокол» в информатике введен для обозначения взаимодействия отдельных элементов в компьютерных сетях. Этот термин ведет свое происхождение от аналогичного термина, принятого в дипломатии. Протокол в дипломатии дает возможность каждой организации беспрепятственно выполнять свои обязанности. Протокол определяет поведение и этикет дипломатических работников, устанавливает правила, относительно официальной и личной переписки. Можно сказать, что дипломатический протокол это совокупность правил, регламентирующих поведение и взаимодействие суверенных государств. Соответственно, протокол компьютерной сети, это совокупность правил, регулирующих взаимодействие параллельно регулирующие объектов сети, с целью обеспечения их согласованного поведения при решении некоторой общей задачи. Представление таких процедур и правил с помощью графической модели конечных автоматов широко применяется в практике для наглядной и строгой спецификации протоколов. В качестве примера рассмотрим классический протокол передачи сообщений «точка-точка» с подтверждением, имеющем название PAR – Positive Acknowledge with Retrains mission. Рис 2.7 Передатчик
Рассмотрим протокол работы передатчика, изображенного на рисунке. Предположим, что автомат-передатчик находится в начальном состоянии S0 и ждет от пользователя порцию данных D, получив которую он переходит в новое состояние S1. В этом состоянии передатчик передает данные в канал связи нумеруя это сообщение D01, и включает таймер t. В состоянии S2, если до срабатывания таймера придет подтверждение правильной передачи Ack, то передатчик перейдет в состояние S3, в противном случае, в состоянии S2 при исчерпании времени работы таймера, он возвращается в состояние S1, и повторно передает сообщение с данными D0. Если он получил подтверждение и находится в состоянии S3, то передатчик снова ожидает событие ввода данных от пользователя, и, получив их, переходит в состояние S4, в котором передает сообщение с номером D1. Если передача завершилась успешно, то в состоянии S5 передатчик ожидает подтверждение от приемника, о получении этого сообщения. Если подтверждение получено, то из положения S5 автомат переходит в положение S0 и цикл передачи повторяется из состояния S0. Если, до срабатывания таймера t, установленного при входе автомата в состояние S5, передатчик не получит подтверждение о приемы предыдущего сообщения, то это сообщение посылается вновь. Аналогично работает приемник. 17. Конечный автомат как модель взаимодействия процессов.
Широко применяемым расширением классической модели конечного автомата являются диаграммы состоянии (Statecharts), введенные Д. Харелом в [8]. Мы рассмотрим две возможности таких «карт состояний». Первая — это гиперсостояние, объединяющее несколько состояний, имеющих идентичную реакцию на одно и то же событие. Вторая возможность — использование «исторического псевдосостояния». Семантика такого состояния (оно обозначается Н) состоит в том, что управление при возврате в гиперсостояние передается тому состоянию, в котором система находилась последний раз прежде, чем она покинула данное гиперсостояние. Переходы между состояниями в такой модели вызываются либо условиями (наступлением истинности предиката над внутренними переменными автомата, например, условие исчерпания буфера), либо событиями. Событиями в диаграммах состояний являются внешние события автомата. Обычно это прием управляющих или информационных сообщений из окружающей среды. Исчерпание тайм-аута также является возможным событием в этом расширении конечно-гоавтомата.
На рис. 3.17, а специфицируется прерывание системы в результате ошибки из любого состояния, принадлежащего гиперсостоянию Working, в состояние Crashed. После восстановления (Recovery) система продолжает работу из того состояния, в котором ее прервал сигнал Crash. В настоящее время модель состояний и переходов интенсивно используется для представления поведения параллельных взаимодействующих процессов.
Параллельные процессы характерны тем, что они функционируют независимо, но при этом должны согласовывать свои действия в определенные моменты для достижения некоторой общей цели. Такие процессы называются кооперирующими, взаимодействующими.
18. Автоматы Мура и Милли. Различают автоматы Мура и автоматы Милли. Автомат Мура является частным случаем более широкого понятия – автомата Мили. Автоматы Мура описываются следующими функциями переходов и выходов: Si+1 = f(Si, xi+1) yi+1 = f(Si+1) Каждое новое состояние автомата Мура обусловлено предшествующим состоянием и входным сигналом, а выходная функция – в каждый данный момент времени однозначно определяется состоянием автомата. Автоматы Мили отличаются от автоматов Мура тем, что выходной сигнал в этом автомате зависит не только от состояния, но и от входного сигнала. Si+1 = f(Si, xi+1) yi+1 = y(si, xi+1) Понятие внутреннего состояния автомата предполагает наличие у автомата внутренней памяти. Число различных эквивалентных состояний зависит от глубины памяти. В качестве элементов памяти могут использоваться стандартные модули ПЗУ или логические схемы с обратными связями в частности – различные типы триггеров.
В принципе любой автомат Мура можно свести к автомату Мили и наоборот. Автомат Мили – более универсальное устройство У автомата Мили нет таких ограничений, которые есть у Мура
Пример конечного автомата Мура представлен на рис. 3.9, а. Здесь выход автомата определяется однозначно тем состоянием, в которое автомат переходит после приема входного сигнала. Например, в состояние si можно прийти по трем переходам: из состояния sO под воздействием Ь, из состояния s2 под воздействием Ь, из состояния si под воздействием а. Во всех трех случаях выходная реакция автомата одна и та же: выходной сигнал у2. Очевидно, что по любому автомату Мура легко построить эквивалентный ему авто-мат Мили; для автомата Мура (рис. 3.9, а) эквивалентный ему автомат Мили изображен на рис. 3.9, б. 19. Примеры конечных автоматов.
Текущее состояние автомата представляет все то, что автомат знает о прошлом с точки зрения его будущего поведения — реакций на последующие входы. Эта история в концентрированном виде определена текущим состоянием, и все будущее поведение автомата, как реакция его на последующие входные сигналы, определено именно текущим состоянием, но не тем, как автомат пришел в него. Итак, конечный автомат — это устройство, работающее в дискретные моменты времени (такты). На вход конечного автомата в каждом такте поступает один из возможных входных сигналов, а на его выходе появляется выходной сигнал, являющийся функцией его текущего состояния и поступившего входного сигнала. Триггер так же является простейшим автоматом. Рассмотрим два типа триггеров: RS-триггер и счетный триггер. Состояние этих автоматов является их выходом, то есть это автоматы Мура. В RS-григгере два входа: Reset и Set. Вход Reset сбрасывает, a Set устанавливает единичное состояние автомата. В счетном триггере единственный счетный вход переключает автомат из нулевого состояния в единичное и обратно.
20. Программная и аппаратная реализация конечных автоматов.
Программная: Ниже приведена реализация конечного автомата, который прибавляет 1 к числу, поданному на вход в виде двоичной записи начиная с младшего разряда. #include <stdio.h> int c;
int main() { goto s1;
s2: c = getchar();
switch(c) { case EOF: exit(0); default: putchar(c); goto s2; } s1: c = getchar(); switch (c) { case EOF: exit(0); case '1': putchar('0'); goto s1; case '0': putchar('1'); goto s2; }
}
Апааратная:
Триггер так же является простейшим автоматом. Рассмотрим два типа триггеров: RS-триггер и счетный триггер. Состояние этих автоматов является их выходом, то есть это автоматы Мура. В RS-григгере два входа: Reset и Set. Вход Reset сбрасывает, a Set устанавливает единичное состояние автомата. В счетном триггере единственный счетный вход переключает автомат из нулевого состояния в единичное и обратно.
21. Сети Петри: принципы построения. Назначение СП: Анализ, моделирование и представление причинно-следственных связей в сложных системах параллельно действующих объ- ектов. Сети Петри были разработаны для моделирования дискретных систем, которые содержат взаимодействующие и параллельно работающие компоненты. Особенно эффективно сети Петри могут быть использованы при моделировании аппаратного и программного обеспечения ЭВМ, моделирования работы гибких производственных систем, а так же моделирования сложных биологических и социальных систем.
Впервые математический аппарат в виде сетей Петри предложил немецкий ученый Карл Адам Петри в своей докторской диссертации «Связь автоматов», которую он защитил в 1962 году. Работа Карла Адама Петри так и оставалась бы академическим исследованием, если бы на эту работу не обратила внимание группа исследователей, работавших под руководством Джорджа Девиса в Массачушесецком технологическом институте. Эта группа использовала математический аппарат, предложенный Петри и применила для работы над проектом MAC. Эта группа внедрила научные исследования, по математическому аппарату сети Петри было сделано много публикаций, которые с этим пор стали широко использоваться. Группа под руководством Джорджа Девиса предложила ряд дополнений и усовершенствований математического аппарата, предложенного Петри, именно в такой форме сети Петри вошли в широкую научную практику.
Полная оценка и использование математического аппарата сетей Петри требует хорошей математической подготовки, что является основным требованием для современного программиста. Современный инженер-програмист должен обладать необходимой математической подготовкой и достаточной квалификацией, чтобы использовать сети Петри как в повседневной инженерной работе, так и в научных исследованиях.
Входы и выходы переходов - комплекты. Комплект - обобщение множества, в которое включены повторяющиеся элементы. Математический аппарат теории сетей Петри основан на теории Комплекта. Теория комплектов является дальнейшим научным развитием теории множеств. Теорию множеств была предожена Георгом Кантером на первом всемирном конгрессе математиков в 1900 году. Георг Кантер определил множество четко и лаконично: «Множество есть многое, мыслимое как единое». Для описания операций с множествами Кантер предложил особый математический аппарат, который в последствии получил название алгебра Кантера. В теории множеств элемент может или принадлежать множеству M или не принадлежать этому множеству. Комплект является набором предметов из некоторой области, в отличие от множества комплекты допускают наличие нескольких экземпляров одного и того же элементы. В отличие от множества, где любой элемент может или не входить в множество или входить в него один только раз, комплект допускает вхождение любого элемента заданное число раз. Пусть область представляет собой совокупность элементов {a, b, c, d}, тогда над этой можно образовать комплект: b1 = {a, b, c}, b2 = { a,d} b3 = {a, a, b, b}, b4 = {a, b, a, b} Таким образом комплекты b1 и b2 являются множествами, комплекты b3 и b4 равны между собой. Так как в комплекте, как и в множестве порядок перечисления элемента не имеет значения. Основным понятием теории комплектов является функция числа вхождения данного экземпляра в комплект. Обозначение #(x, B) означает количество вхождения элемента в комплект B, то есть число экземпляров x в комплекте B. Если ограничить число элементов в комплекте следующим образом: 0 <= #(x, B) <= 1, то все комплекты будут множествами. Элемент x является членом комплекта B, если #(x, B) > 0 Так же как и в теории множеств, в теории комплектов существует пустой комплект, не содержащий элементов.
#(x, B) = 0 В пустом комплекте для всех элементов x содержание элементов равно нулю. Под мощностью |B| понимается количество всех элементов |B| = сигма(индекс x)(x,B)
Комплект А является подкомплектом, если для любого элемента х, количество каждого элемента в копмлекте А меньше, чем комплекта В. A В предельном случае два комплекта равны тогда, когда количество любого элемента х в комплекте А равно количеству элементов х в комплекте В для всех х. A = B Комплект А строго включен в комплект В, если А меньше или равно В и А неравно В А Операции над комплектами В отличии от теории множеств, над комплектами определены 4 операции. Если заданы два комплекта А и В, то для них существуют следующие операции: 1) Объединение AUB: max(#(x,A), #(x,B)) Объединение комплектов отличается от объединения в теории множеств. 2) Пересечение А П B: min(#(x,A), #(x,B)) 3) Сумма А + В = #(x,A) + #(x,B)) 4) Разность А - В = #(x,A) - #(x,B)) В теории множеств – суммы и разности множеств не существует. В разности комплектов необходимо, чтобы число элементов в комплекте А было больше чем число элементов в комплекте В, т.к. число элементов в комплекте не может быть отрицательным. Можно показать, что объединение комплектов, пересечение комплектов и сумма комплектов как математические операции коммутативны и ассоциативны. Справедливо следующее соотношение: А П В A П В A – B |A U B| <= |A| + |B| |A + B| = |A| + |B| Доказать геометрическим методом или методом рассуждения. Назовем множество элементов, из которых составлены комплекты областью D. Пространство комплектов Dn – есть множество всех таких комплектов, что их элементы принадлежат D и ни один из элементов не входит в комплект более n раз. Иначе говоря, для любого комплекта можно записать соотношение: B Множество D 23. Структура сети Петри. Сеть Петри состоит из 4-ех компонентов, которые и определяют ее структуру: 1) Множество P (от слова position) 2) Множество переходов T (transition) 3) Входная функция I (in) 4) Выходная функция O (out) Входная и выходная функции связаны с переходами и позициями. Входная функция I отображает переход Tj в множество позиций I(tj), называемых входными позициями перехода. Выходная функция O отображает переход Tj в множество позиций O(tj), называемых выходными позициями перехода. I: Tj à P O: Tj à P Определение: Сеть Петри С является четверкой мат. объектов C = (P, T, I,O), где: P = {p1,p2,…,pn} T = {t1, t2, …, tn} Множество позиций и переходов не пересекается. Входная функция является отображением перехода в множество позиций I: Tj à P Выходная O является отображением из конкретного перехода в множество позиций O: Tj à P Мощность множества P есть число N. А мощность множество T, если число M. Произвольный элемент из множества позиций P обозначается как pi (i = 1,2,…,n) Произвольный элемент T обознается, как tj. (j = 1,2,…,n) Входы и выходы переходов представляют из себя комплекты позиции. Кратность входной позиции для перехода tj есть число появления позиции pi во входном комплекте переходов: #(pi I(tj)) Аналогично, кратность выходной позиции pi для перехода tj есть число появлений позиции pi в выходном комплекте переходов: #(pi, O(tj)) Определение 3.2. Определим расширенную функцию I и выходную функцию O: #(tj I(pi) = #(pj O(tj)) #(tj O(pi) = #(pi I(tj))
[ОФТОПИК] Назовем множество элементов, из которых составлены комплекты областью D. Пространство комплектов Dn – есть множество всех таких комплектов, что их элементы принадлежат D и ни один из элементов не входит в комплект более n раз. Иначе говоря, для любого комплекта можно записать соотношение: B Множество D
24. Графы сети Петри. Графы сетей Петри
Для иллюстрации основных понятий теории сетей Петри удобным представлением является графическое представление сети Петри.
Теоретико - графовым представлением сети Петри двудольный (бинарный) ориентированный мультиграф.
Двудольность (бинарность) графа состоит в том, что вершины графического представления бывают двух типов: 1) В виде кружка обозначается позиция 2) В виде планки – изображается переход Причем дуги соединяют только вершины различных типов, т.е. кружок соединяется с только с планкой, планка соединяется только с кружком.
Ориентированные дуги соединяют позиции и переходы.
Дуга направленная от позиции pi к переходу tj определяет позицю, которая является входом перехода …: O à|
Выходная позиция указывается дугой от перехода к позиции
Кратные выходы, так же представлены кратными дугами.
Граф G = (V, A) сети Петри есть бинарный ориентированный мультиграф.
Где V = { v1, v2,…, vs } – множество вершин. A = { a1, a2,…, ar } – множество дуг.
ai = (vj, vk), где vj и vk
Множество V состоит из двух непересекающихся подмножеств P и T à vj ∈ P и vk ∈ T или vj ∈ T и vk ∈ P
Граф сети Петри являетс мультиграфом, т.к. он допускает существование кратных дуг. Количество кратных дуг специально оговаривается.
Определим V = P U T. Зададим множество А как комплект направленных дуг такой, что для всех pi c P и tj с T выполняются след. соотношения:
#((pi, tj), A) = #(pi, I(tj)) 25.Аналитическое и графическое представление сети Петри. Представление сети Петри в виде структуры и в виде графа
Пусть задана следующая структура сети Петри C = (P,T,I,O), n = 5, m = 4;
P = {p1,p2,p3,p4,p5} T = {t1,t2,t3,t4}
I(t1) = {p1} I(t2) = {p2, p3, p5} I(t3) = {p3}
O(t1) = {p2, p3, p5} O(t2) = {p5} O(t3) = {p4} O(t4) = {p2, p3}
На этой сети всегда можно составить структуру сети Петри. Оба представления сети Петри в виде структуры и в виде Графа эквивалентны. Их можно преобразовать в друг друга.
Расширенные функции:
I(p1) = {} I(p2) = {t1, t4} I(p3) = {t1, t4} I(p5) = {t1, t2}
O(p1) = {t1} O(p2) = {t2} O(p3) = {t2, t3} O(p4) = {t4} O(p5) = {t2}
[ОФТОПИК]Заметим, что в случае дуг большой кратности для представления используется пучок дуг, помеченный числом кратности, а не изображением всех дуг, как показано на рис. 3.6. O –8->| -12->
Маркировка ню есть присваивание фишек позициям сети Петри. Фишка – это одна из компонент сети Петри (подобно позициям и переходам). Фишки присваиваются позициям. Их количество при выполнении сети может изменяться. Фишки используются для отображения динамики системы.
Маркировка ню сети Петри С = (Р, Т, И, О) есть функция, отображающая множество позиций Р в множество неотрицательных целых чисел N: ню: P à N Маркировка ню может быть также определена как n вектор ню = (м1, м2,…, мн), где н = |P| и каждое нюi Э N, i = 1…n
Вектор ню определяет для каждой позиции pi сети Петри количество фишек в этой позиции, т.е. количество фишек в позиции pi есть нюi, i = 1…n. Очевидно, что ню(pi) = нюi и этим выражением устанавливается связь между определением маркировки как вектора и как функции.
Маркированная сеть Петри C = <P, T, I, O, m > есть совокупность структуры сети Петри <P, T, I, O> и маркировки m.
Определение. Переход tj в маркированной СП с маркировкой m может быть запущен всякий раз, когда он разрешён. В результате запуска разрешённого перехода tj образуется новая маркировка m’, определяемая следующим соотношением: m’(pi) = m(pi) – #(pi, I(tj)) + #(pi, O(tj)).
27.Выполнение сети Петри.
Выполнением упраляют количество и распределение фишек. Сеть выполняется посредством запуска переходов. Переход запускается когда он разрешен. Переход разрешен, если каждая из его входных позиций имеет число фишек по крайней мере равное числу ребер из позиции в переход Кратные фишки необходимы для кратных входных дуг. Фишки во входной позиции, которые разрешают переход, называются его разрешающими фишками. Например, если позиции р1 и р2 служат входами для перехода t4, тогда t4 разрешен, если р1 и р2 имеют хотя бы по одной фиш- ке. Для перехода t7 с входным комплектом {p6, p6, p6} позиция р6 должна обладать по крайней мере тремя фишками, для того чтобы t7 был разрешен. Определение. Переход tj ∈Т в маркированной сети Петри С = (Р, Т, I, О) с маркировкой µ разрешен, если для всех pi ∈P, µ (pi) ≥ # (pi, I(tj)). Переход запускается удалением всех разрешающих фишек из его входных позиций и последующим помещением в каждую из его выходных позиций по одной фишке для каждой дуги. Кратные фишки создаются для кратных выходных дуг. Например, переход t3 с I(t3) = {p2} и О(t3) = {p7, р13} разрешен всякий раз, когда в р2 будет хотя бы одна фишка. Переход t3 запускается удалением одной фишки из позиции р2 и помещением одной фишки в позицию р7 и в р13 (его выходы). Дополнительные фишки в позиции р2 не влияют на запуск t3 (хотя они могут разрешать дополнительные запуски t3). Переход t2, в котором I(t2) = {p21, р23} и О(t2) = {p23, р25, р25} запускается удалением одной фишки из р21 и одной фишки из р23, при этом одна фишка помещается в р23 и две в р25 (т. к. р25 имеет кратность, равную двум). Запуск перехода в целом заменяет маркировку µ сети Петри на новую маркировку µ′. Так как можно запустить только разрешенный переход, то при запуске перехода количество фишек в каждой позиции всегда остается неотрицательным. Запуск перехода никогда не удалит фишку, отсутствующую во входной позиции. Если какая-либо входная позиция перехода не обладает достаточным количеством фишек, то переход не разрешен и не может быть запущен.
Определение. Переход tj в маркированной сети Петри с маркировкой µ может быть запущен всякий раз, когда он разрешен. В результате запуска разрешенного перехода tj образуется новая маркировка µ′, определяемая следующим соотношением: µ′(pi) = µ(pi) – # (pi, I(tj)) + # (pi, O(tj)). 28. Пространство состояний сети Петри. Состояние сети Петри определяется маркировкой. Функция следующего состояния δ: N n × T → N n для сети C = (P, T, I, O) определена, если µ(pi) ≥ #(pi, I(ti)) δ(µ, tj) = µ’ = µ(pi) − #(pi, I(tj)) + #(pi, O(tj)) При выполнении сети получаем: • последовательность маркировок - (µ0, µ1, µ2,...) • последовательность переходов - (t0, t1, t2,...) Инвариант: δ(µk, tk) = µk+1 \Состояние сети Петри определяется ее маркировкой. Запуск перехода изменяет состояние сети Петри посредством изменения маркировки сети. Пространство состояний сети Петри, обладающей n позициями, есть множество всех маркировок, т, е. Nn. Изменение в состоянии, вызванное запуском перехода, определяется функцией изменения б, которую мы назовем функцией следующего состояния. Когда эта функция применяется к маркировке µ (состоянию) и переходу tjt она образует новую маркировку (состояние), которая получается при запуске перехода tj в маркировке µ. Так как tj может быть запущен только в том случае, когда он разрешен, то функция б(µ, tj) не определена, если tj не разрешен в марки ровке µ. Если же tj разрешен, то 6(µ, t}) = µ', где µ' есть маркировка полученная в результате удаления фишек из входов tj и добавления фишек в выходы t}. Определение 2.8. Функция следующего состояния б: Nn X Т -> -> Nn для сети Петри С = (Р, Т, I, О) с маркировкой µ и переходом tj? Т определена тогда и только тогда, когда µ(pi) >= #(pi, I(tj)) для всех p i £ Р. Если 6(µ, fj) определена, то б(µ, tj) = µ', где µ'(pi) = µ(pi)-#(pi,I(tj)) + #(рi, 0(tj)) для всех pi £ Р. Пусть дана сеть Петри С = (Р, Т, I, О) с начальной маркировкой µ°. Эта сеть может быть выполнена последовательными запусками переходов. Запуск разрешенного перехода tj в начальной маркировке образует новую маркировку р1 = 6(µ°, tj). В этой новой маркировке можно запустить любой другой разрешенный переход, например tk, образующий новую маркировку µ2 = 6(µ1, tk). Этот процесс будет продолжаться до тех пор, пока в маркировке будет существовать хотя бы один разрешенный переход. Если же получена маркировка, в которой ни один переход не разрешен, то никакой переход не может быть запущен, функция следующего состояния не определена для всех переходов, и выполнение сети должно быть закончено. При выполнении сети Петри получаются две последовательности: последовательность маркировок (µ°, µ1, µ2,...) и последовательность переходов, которые были запущены (tj0, tj1, tj3,...). Эти две последовательности связаны следующим соотношением: 6(µk, tjk) = pk+1 для k = 0, 1, 2,.... Имея последовательность переходов и р°, легко получить последовательность маркировок сети Петри, а имея последовательность маркировок, легко получить последовательность переходов, за исключением нескольких вырожденных случаев'). Таким образом, обе эти последовательности представляют описание выполнения сети Петри. Пусть некоторый переход в маркировке µ разрешен и, следовательно, может быть запущен. Результат запуска перехода в маркировке р есть новая маркировка µ'. Говорят, что µ' является непосредственно достижимой из маркировки µ, иными словами, состояние µ' непосредственно получается из состояния µ. 29,30,40 Достижимость сети Петри. + 30.Множество достижимости сети Петри Достижимость в сети Петри Для сети C = (P, T, I, O) и µ маркировка µ’ называется непосредственно достижимой из µ, если ∃ tj ∈ T, δ(µ, tj) = µ’. Множество достижимости R(C, µ) - наименьшее множиство маркировок определенных следующим образом: 1. µ Є R(C, µ); 2. если µ' Є R(C, µ) и µ'' = б(µ',tj) для некоторого tj Є T, то µ'' Є R(C, µ).
R(C, µ) = {(1, 0, n), (0, 1, n)|n ≥ 0} ПОДРОБНЫЙ ТЕКСТ: Определение 1. Для сети Петри С = (Р,Т,I,О, µ) с маркировкой µ маркировка µ'называется непосредственно достижимой из µ, если существует переход tj Є T, такой, что б(µ,tj) = µ'. Это понятие легко распространить на определение множества достижимых маркировок данной сети Петри. Если µ' непосредственно достижима из µ', а µ'' из µ', то говорят, что µ''достижима из µ. Определим множество достижимости R(C, µ) сети Петри С с маркировкой µ как множество всех маркировок, достижимых из µ. Маркировка µ' принадлежит R(C, µ), если существует какая либо последовательность запусков переходов, изменяющих µ на µ'. Отношение "достижимости" является рефлексивным и транзитивным бинарным отношением. Определение 2. Множество достижимости R(C, µ)для сети Петри С = (P,T,I,O, µ)с маркировкой µесть наименьшее множество маркировок определенных следующим образом: 1. µ Є R(C, µ); 2. если µ' Є R(C, µ) и µ'' = б(µ',tj) для некоторого tj Є T, то µ'' Є R(C, µ). Пример: рассмотрим сеть Петри. Если маркировка µ = (1,0,0), то непосредственно достижимы две маркировки: (0,1,0) и (1,0,1). Из (0,1,0) нельзя достичь ни одной маркировки, т.к. ни один переход не разрешен. Из (1,0,1) можно получить (0,1,1) и (1,0,2). Вообще говоря, можно показать, что множество достижимости R(C, µ) для этой сети имеет вид: {(1,0,n), (0,1,n)| n>=0} Для удобства можно распространить функцию следующего состояния на отображение маркировки и последовательности переходов в новую маркировку. Для последовательности переходов (tj1,tj2,…,tjk) и маркировки µ маркировка µ' = б(µ, tj1,tj2,…,tjk) является результатом запусков сначала tl, затем t2 и т.д. до tjk. Определение 3. Расширенная функция следующего состояния определяется для маркировки µ и последовательности переходов δ Є Т* следующими соотношениями: δ(µ,tj,σ) = δ(δ(µ,tj),σ), где Т* - множество всех подмножеств множества (булеан множеств) переходов в Т.
31. Сети Петри как аппарат для моделирования систем
Моделирование и сети Петри Для моделирования событий в системе. Классы систем: • аппаратное обеспечение ЭВМ; • программное обеспечение ЭВМ; • физические системы; • социальные системы.
События и условия Событие - дейстие, имеющее место в системе. Состояние системы - множество условий. Условие - предикат или логическое описание состояния си- стемы. Предусловия события - условия необходимые для того, что- бы событие могло произойти. Постусловия - условия, к которым приводит событие. Представление системы сетью Петри базируется на двух понятиях: событиях и условиях. Под событием понимается действие, имеющее место в системе. Появление события определяет состояние системы, которое может быть описано множеством условий. Условие - это предикат или логическое описание состояния системы. При этом условие может принимать либо значение "истина", либо значение "ложь". Для того, чтобы событие произошло, необходимо выполнение соответствующих условий, которые называются предусловиями события. Возникновение события может привести к появлению постусловий. В сети Петри условия моделируются позициями, события - переходами. При этом входы перехода являются предусловиями соответствующего события, выходы - постусловиями. Возникновение события равносильно запуску соответствующего перехода. Выполнение условия представляется фишкой (маркером) в позиции, соответствующей этому условию. Запуск перехода удаляет разрешающие маркеры, представляющие выполнение предусловий и образует новые маркеры, которые представляют выполнение постусловий. Построение моделей систем в виде сетей Петри связано со следующими обстоятельствами: 1. Моделируемые процессы (явления) совершаются в системе, описываемой множеством событий и условий, которые эти события определяют, а также причинно - следственными отношениями, устанавливаемыми на множестве "события - условия". 2. Определяются события - действия, последовательность наступления которых управляется состоянием системы. Состояния системы задаются множеством условий. Условия формулируются в виде предикатов. Количественные условия характеризуются емкостью. Емкость условий выражается числами натурального ряда. 3. Условия (предикаты) могут быть выполнены или не выполнены. Только выполнение условий обеспечивает возможность наступления событий (предусловия). 4. После наступления события обеспечивается выполнение других условий, находящихся с предусловиями в причинно - следственной связи (постусловия). После того, как событие имело место, реализуются постусловия, которые в свою очередь являются предусловиями следующего события и т.д. Пример. Автомат-продавец Условия: а) ждет, б) заказ прибыл и ждет, в) автомат выполняет заказ, г) заказ выполнен. События: 1. Заказ поступил. 2. Автомат начинает выполнять заказ. 3. Автомат заканчивает выполнение заказа. 4. Заказ доставляется
Условия - позиции. События - переходы.
. 32. Одновременность и конфликт сети Петри.
Одной из особенностей сетей Петри и их моделей является параллелизм или одновременность. В модели сети Петри два разрешенных взаимодействующих события могут происходить независимо друг от друга, но при необходимости их легко синхронизировать. Т.о. сети Петри представляются идеальными для моделирования систем с распределенным управлением, в которых несколько процессов выполняются одновременно. Другая важная особенность сетей Петри - их асинхронная природа. В сети Петри отсутствует измерение времени или течение времени. Структура сетей такова, что содержит в себе информацию для определения возможных последовательностей событий. В этих моделях нет никакой информации,
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 465; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.10.152 (0.012 с.) |


 На рис. 3.17 показано, как с помощью этих простых расширений удается наглядно представить сложное поведение.
На рис. 3.17 показано, как с помощью этих простых расширений удается наглядно представить сложное поведение.
 Опишем поведение родителя, отправившего сына в школу. Сын приносит двойки и пятерки. Отец не хочет хвататься за ремень каждый раз, как только сын получит очередную двойку, и выбирает более тонкую тактику воспитания. Задавать автомат удобно графом, в котором вершины соответствуют состояниям, а ребро из состояния s в состояние q, помеченное х/у, проводится тогда, когда автомат из состояния s под воздействием входного сигнала х переходит в состояние q с выходной реакцией у. Граф автомата, моделирующего умное поведение родителя, представлен на рис. 3.2..Этот автомат имеет четыре состояния {sO, si, s2, s3} и два входных сигнала — оценки, полученные сыном в школе: {2,5}. Начиная с начального состояния sO (оно помечено входной стрелкой), автомат под воздействием входных сигналов переходит из одного состояния в другое и выдает выходные сигналы — реакции на входы. Выходы автомата {уО,..., у5} будем интерпретировать как действия родителя так: y0: брать ремень; y1: ругать сына; у2: — успокаивать сына; уЗ: — надеяться; у4: — радоваться; у5: — ликовать. Сына, получившего одну и ту же оценку — двойку, ожидает дома совершенно различная реакция отца в зависимости от предыстории его учебы. Отец помнит, как его сын учился раньше, и строит свое воспитание с учетом его предыдущих успехов и неудач. Например, после третьей двойки в истории 2,2,2 сына встретят ремнем, а в истории 2, 2, 5, 2 — будут успокаивать. Каждая предыстория определяет текущее состояние автомата, при этом некоторые входные предыстории эквивалентны (именно те, которые приводят автомат в одно и то же состояние): история 2,2,5 эквивалентна пустой истории, которой соответствует начальное состояние.
Опишем поведение родителя, отправившего сына в школу. Сын приносит двойки и пятерки. Отец не хочет хвататься за ремень каждый раз, как только сын получит очередную двойку, и выбирает более тонкую тактику воспитания. Задавать автомат удобно графом, в котором вершины соответствуют состояниям, а ребро из состояния s в состояние q, помеченное х/у, проводится тогда, когда автомат из состояния s под воздействием входного сигнала х переходит в состояние q с выходной реакцией у. Граф автомата, моделирующего умное поведение родителя, представлен на рис. 3.2..Этот автомат имеет четыре состояния {sO, si, s2, s3} и два входных сигнала — оценки, полученные сыном в школе: {2,5}. Начиная с начального состояния sO (оно помечено входной стрелкой), автомат под воздействием входных сигналов переходит из одного состояния в другое и выдает выходные сигналы — реакции на входы. Выходы автомата {уО,..., у5} будем интерпретировать как действия родителя так: y0: брать ремень; y1: ругать сына; у2: — успокаивать сына; уЗ: — надеяться; у4: — радоваться; у5: — ликовать. Сына, получившего одну и ту же оценку — двойку, ожидает дома совершенно различная реакция отца в зависимости от предыстории его учебы. Отец помнит, как его сын учился раньше, и строит свое воспитание с учетом его предыдущих успехов и неудач. Например, после третьей двойки в истории 2,2,2 сына встретят ремнем, а в истории 2, 2, 5, 2 — будут успокаивать. Каждая предыстория определяет текущее состояние автомата, при этом некоторые входные предыстории эквивалентны (именно те, которые приводят автомат в одно и то же состояние): история 2,2,5 эквивалентна пустой истории, которой соответствует начальное состояние.


 B
B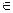 Dn
Dn есть множество всех комплектов над областью D без какого либо ограничения на число экзмеляров элементов в комплекте.
есть множество всех комплектов над областью D без какого либо ограничения на число экзмеляров элементов в комплекте. V
V


 .
.


