
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обобщенная математическая модель объекта проектированияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Рассмотрим обобщенную математическую модель объекта проектирования вне зависимости от предметной области, которой он принадлежит. Это позволит на достаточно абстрактном уровне выявить структуру объекта проектирования, его внешние связи с общей концептуальной схемой процесса проектирования, сформулировать основные задачи проектирования. Обобщенную математическую модель объекта проектирования в наиболее общем (абстрактном) виде можно представить следующим образом (см. рис. 1.2).
Рис 1.2. Обобщенная математическая модель объекта
Элементами обобщенной математической модели являются: 1) множество Х варьируемых параметров объекта проектирования; 2) множество Y входных независимых сигналов (параметров), определяющих внешние условия, в которых должен функционировать объект проектирования; 3) оператор L, определяющий операции над параметрами Х и Y; 4) множество выходных сигналов (показателей) G(X, Y). Один из них может быть переведен в ранг целевой функции S(X, Y). При этом под оператором L понимается полная система математических операций, описывающая численные или логические соотношения между множеством входных сигналов, т.е. X и Y, и множеством выходных сигналов, т.е. показателей G(X,Y). Связи объекта с внешней средой задаются: 1) входными сигналами (связями); 2) выходными сигналами (показателями). К входным сигналам, очевидно, относятся совокупности независимых входных сигналов К выходным сигналам объекта проектирования относится совокупность критериальных показателей Множество независимых входных сигналов 1) технические параметры объекта, не подлежащие по замыслу изменению (вариации) в процессе проектирования (они определены исходя из условий вхождения объекта проектирования в систему более высокого уровня иерархии; 2) физические возмущения среды, с которой взаимодействует объект проектирования (изменения температуры, давления и т.п.); 3) тактические параметры, такие как диапазоны высот, скоростей и т.п. в которых должен функционировать объект. Применительно к этапу проектирования среда функционирования объекта может быть названа средой проектирования. С позиции организации процесса проектирования определяющими являются такие понятия, как определенность и неопределенность среды проектирования. Рассмотрим эти понятия. Для этого отметим, что совокупность входных независимых сигналов может быть задана или набором констант или системой величин, каждая из которых имеет диапазон значений, В первом случае система входных независимых сигналов отображается в виде вектора (точки) Понятия определенная и неопределенная среда проектирования можно проиллюстрировать следующим образом (см. Рис. 1.3)
Подобная классификация имеет принципиальное значение для расчета критериальных функций При определенной среде значение каждого компонента
где При неопределенной среде проектирования пространство возможных значений входных независимых сигналов После этого значения критериальных функций на
Обобщающий оператор Z зависит от выбранных критериев синтеза. Обычно в практике проектирования систем с неопределенной средой проектирования используются два основных критерия синтеза: по наихудшим критическим значениям Gj или S или по среднеквадратическому значению этих функций, обобщенному по всему пространству Ry. Множество X ={хi}, i = 1,n варьируемых параметров проектируемого объекта отображается пространством варьируемых параметров Rх. Поиск в этом пространстве является одной из составляющих задачи проектирования. Пространство Rх, метрическое с размерностью, равной числу варьируемых параметров. Критериальные условия типа равенства Gj(X) = Gj0 образуют в пространстве Rх поверхности ограничения. Условия типа Gj(X) <= Gj0 образуют пространство вида При корректно сформулированной задаче синтеза в пространстве
Рис.1 4. Сечение критериальных функций в двумерном пространстве Rx.
Х0y — точка условного экстремума — оптимальное решение, Х0 — безусловный экстремум целевой функции Если все компоненты пространства Множество выходных сигналов (параметров) объекта проектирования образует пространство RG критериальных показателей. Одна из осей этого пространства может содержать целевую функцию S. Множество векторов Определяющими характеристиками критериальных показателей с точки зрения постановки задачи и организации поиска является: 1) число критериальных показателей, 2) их однородность, 3) вид критериальных функций в пространстве варьируемых параметров, 4) способ обобщения критериальных показателей в пространстве независимых входных сигналов. По числу критериальных показателей объекты проектирования делят на однокритериальные и многокритериальные. При многокритериальных задачах возникает проблема предпочтения того или иного критерия, связанная с постановкой задачи синтеза и выбора метода поиска решения в многомерных пространствах при наличии многих критериальных функций. Однородность критериев позволяет в ряде случаев привести их нормировку и свести многокритериальную задачу к однокритериальной задаче. По виду критериальных функций в пространстве Rx0 проектируемые объекты соответствуют задачам с однозначными и многозначными решениями. Для однозначных характерны условия выпуклости всех критериальных функций в пространстве Rx0, (см. рис. 1.4). Многозначность связана с многоэкстремальностью хотя бы одной из критериальных функций. Это приводит либо к разрыву пространства допустимых решений Rx0 на локальные пространства, либо к появлению в Rx0 ряда условных экстремумов. В обоих случаях решение при различных начальных условиях поиска
4 б) Рис. 1.5. Примеры многозначных решений: a) Rx0, представляется локальными областями b) целевая функция S(X) многоэкстремальная Многозначность решений приводит к попыткам глобального поиска, т.е. нахождению наилучшего решения в пространстве Rx0. При оптимальном проектировании один из критериальных показателей переводится в ранг целевой функции S, и тогда критерии проектирования запишутся в виде: обеспечить extr S при Техническое решение для проектируемого объекта ищется на некотором множестве структур А, которые может создать разработчик, и на множестве точек пространства варьируемых параметров Rx0, задаваемого разработчиком. Множество структур А и пространство Rx0 образуют множество альтернатив, на котором ищется решение. При этих обозначениях задачу проектирования можно сформулировать так: найти такие
при заданной среде функционирования Y. Техническое решение при этом представляет структуру А0 и вектор X0y, найденные из множества возможных структур и варьируемых параметров, отвечающие заданным критериям и среде функционирования объекта. Таким образом, реализация задачи проектирования в общем случае сводится к процедурам структурного параметрического синтеза, которые являются итерационными и образуют два цикла: - внешний цикл структурного синтеза, - внутренний цикл параметрического синтеза. Последовательность смены процедур структурного и параметрического синтеза при автоматизированном проектировании можно представить в виде схемы (см. рис. 1.6). Схема предполагает перебор структур и параметров до момента получения решения, удовлетворяющего критериальным условиям (точка 1). При невозможности найти решение на обозримом числе структур в пределах заданного пространства поиска (точка 2) система проектирования выходит на процедуру принятия решения, которая содержит два варианта. По первому варианту (так называемая альтернатива разработчика) разработчик расширяет пространство Rx0 за счёт перевода ряда независимых параметров Y в разряд варьируемых и осуществляет поиск новых структур за счёт расширения множества А. По второму варианту (так называемая альтернатива заказчика) заказчик за счет изменения вектора
Рис. 1.6. Схема смены процедур структурного и параметрического синтеза
|
||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 1061; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |


 и совокупность варьируемых технических параметров объекта проектирования
и совокупность варьируемых технических параметров объекта проектирования  .
.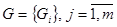 , необходимых для оценки принимаемых решений. Один из таких показателей может быть переведен в ранг целевой функции S, для которого необходимо обеспечить при проектировании экстремального значения.
, необходимых для оценки принимаемых решений. Один из таких показателей может быть переведен в ранг целевой функции S, для которого необходимо обеспечить при проектировании экстремального значения. . Во втором - в виде области (системы точек) этого пространства
. Во втором - в виде области (системы точек) этого пространства  .В зависимости от того, как описываются входные независимые сигналы, т.е. вектором
.В зависимости от того, как описываются входные независимые сигналы, т.е. вектором  или пространством
или пространством  Рис. 1.3. Определенная (а) и неопределенная среда (б) проектирования
Рис. 1.3. Определенная (а) и неопределенная среда (б) проектирования .
.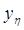 вектора Y задается числом. Поэтому на каждом l -м цикле проектирования значения критериальных функций находят в следующем виде:
вектора Y задается числом. Поэтому на каждом l -м цикле проектирования значения критериальных функций находят в следующем виде: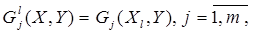
 - вектор варьируемых параметров Х в
- вектор варьируемых параметров Х в  -м цикле проектирования,
-м цикле проектирования,  ,
,  - вектор независимых входных сигналов, заданный в виде системы констант
- вектор независимых входных сигналов, заданный в виде системы констант  , m - число критериальных показателей, H – число элементов вектора Y.
, m - число критериальных показателей, H – число элементов вектора Y. - мощность множества
- мощность множества  .
.
 ограниченное поверхностями. Это пространство
ограниченное поверхностями. Это пространство  является допустимым техническим решением.
является допустимым техническим решением. находится точка, при которой целевая функция S(X) достигает условного экстремума. Эта точка представляет вектор оптимального технического решения X0у (см. рис. 1.4).
находится точка, при которой целевая функция S(X) достигает условного экстремума. Эта точка представляет вектор оптимального технического решения X0у (см. рис. 1.4).
 — подпространство допустимых решений,
— подпространство допустимых решений, являются независимыми, т.е. каждый компонент не связан функциональной связью с любым другим компонентом рассматриваемого пространства, то оси пространства образуют ортогональный базис параметрического синтеза. Физически это означает, что изменение любого параметра не влечёт за собой автоматическое изменение другого.
являются независимыми, т.е. каждый компонент не связан функциональной связью с любым другим компонентом рассматриваемого пространства, то оси пространства образуют ортогональный базис параметрического синтеза. Физически это означает, что изменение любого параметра не влечёт за собой автоматическое изменение другого. пространства
пространства  , образованных на допустимой совокупности множеств варьируемых и независимых параметров X и Y, определяет m -мерное пространство функционирования объекта данной структуры -
, образованных на допустимой совокупности множеств варьируемых и независимых параметров X и Y, определяет m -мерное пространство функционирования объекта данной структуры -  . В пространстве
. В пространстве  — область допустимых значений
— область допустимых значений  находящуюся в отношениях соответствия пространству допустимых решений
находящуюся в отношениях соответствия пространству допустимых решений 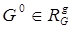 , определяющая максимум (или минимум) целевой функции, соответствует оптимальному решению
, определяющая максимум (или минимум) целевой функции, соответствует оптимальному решению  .
.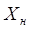 "скатываются" в различные стационарные точки
"скатываются" в различные стационарные точки  (см. рис. 1.5).
(см. рис. 1.5).
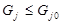 и заданной среде функционирования Y.
и заданной среде функционирования Y.
 снижает требования, предъявляемые к проектируемому объекту.
снижает требования, предъявляемые к проектируемому объекту.



