
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
С.Ю. Свидченко, Т.Г. КоролеваСодержание книги Поиск на нашем сайте
С.Ю. Свидченко, Т.Г. Королева
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ЭЛЕКТРОТЕХНИКИ Часть 1 Методические указания по выполнению лабораторных работ
Дисциплина – «Теоретические основы электротехники» Специальности: 181300 «Электрооборудование и электрохозяйство 150200 «Автомобили и автомобильное хозяйство»
Печатается по решению редакционно-
Орел 2002 Авторы: доцент, кандидат технических наук С.Ю. Свидченко доцент, кандидат технических наук Т.Г. Королева
Рецензент: доцент, кандидат технических наук В.А. Гринин
Методические указания содержат программы выполнения четырёх лабораторных работ по разделу «Основы теории линейных электрических цепей», являющемуся начальной частью дисциплины «Теоретические основы электротехники», изучаемой в соответствии с учебным планом специальностей 150200 и 181300. Полностью или частично эти лабораторные работы выполняются в рамках изучения дисциплин «Теоретическая электротехника», «Электротехника», «Электротехника, электроника, электрооборудование», «Электротехника, электроника и электропривод», «Общая электротехника», «Общая электротехника и электроника», «Инженерное оборудование и электроснабжение», «Электротехника и электроника» студентами, обучающимися по специальностям 071100, 120100, 120100у, 120200, 120300, 120400, 170600, 170900, 190100, 190600, 200800, 210200, 220500, 270300, 270800, 271100, 280800, 280900, 290300, 290500, 551800. В методических указаниях приведены также краткие теоретические сведения, описание оборудования и контрольные вопросы к каждой работе. Указания предназначены для студентов очной и очно-заочной форм обучения соответствующих специальностей.
Редактор Т.Д. Васильева Технический редактор Т.П. Прокудина Орловский государственный технический университет Лицензия ИД № 00670 от 05.01.2000
Подписано к печати 25.05.2002 г. Формат 60х84 1/16. Печать офсетная. Уч.- изд. л. 2,7. Усл. печ. л. 2,8. Тираж 300.
Отпечатано с готового оригинал-макета на полиграфической базе ОрелГТУ, 302030, г. Орел, ул. Московская, 65.
© ОрелГТУ, 2002 © Свидченко С.Ю., Королева Т.Г., 2002
Содержание
Стр.
Лабораторная работа №1. Методы анализа электрических
Лабораторная работа №2. Линейная неразветвлённая цепь Лабораторная работа №3. Линейная разветвлённая цепь синусоидального тока............................................................................... 24 Лабораторная работа №4. Трёхфазные цепи синусоидального
ЛАБОРАТОРНАЯ РАБОТА № 1
МЕТОДЫ АНАЛИЗА ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ Цели работы 1.1 Экспериментальная проверка справедливости эквивалентных преобразований схем электрических цепей. 1.2 Закрепление практических навыков использования методов анализа электрических цепей. Экспериментальная проверка результатов расчёта.
Теоретические сведения Электрические цепи делятся на простые и сложные. К признакам, определяющим простую цепь, можно отнести: - наличие только одного источника энергии (сигнала); - возможность до расчётов указать истинные направления токов во всех ветвях; - соединение элементов цепи выполнено по правилам последовательного, параллельного и смешанного соединений. Отсутствие любого из этих признаков может переводить цепь в категорию сложных. Для анализа простых цепей используется два метода (в работе используется первый): - метод свёртки схемы цепи относительно зажимов источника (он же метод определения входного или эквивалентного сопротивления); - метод пропорциональных (определяющих) величин. Из многих методов анализа сложных цепей здесь рассматриваются два: метод контурных токов (МКТ) и метод узловых напряжений (МУН). Все методы, рассматриваемые в работе, применены к цепям постоянного тока, однако они справедливы и в цепях переменного тока. Метод свёртки простых цепей основан на возможности эквивалентных преобразований участков цепи. Преобразуемый участок заменяется на комбинацию (чаще всего более простую) других элементов. Причём, параметры новых элементов определяются из условия сохранения энергетического состояния цепи за пределами преобразуемого участка. Чаще всего используются эквивалентные преобразования, представленные на рисунке 1.1.
в
Рисунок 1.1 - Схемы эквивалентных преобразований: Метод контурных токов. Этот метод позволяет уменьшить количество уравнений системы, составляемых по законам Кирхгофа, до
где
Он основан на том, что ток в любой ветви цепи можно представить в виде алгебраической суммы контурных токов, протекающих по этой ветви. При использовании метода перед расчётом выбирают направления и путь протекания контурных токов – по любой ветви должен протекать хотя бы один выбранный контурный ток. Общее число неизвестных контурных токов определяется величиной Кроме того, Для определения неизвестных контурных токов система уравнений составляется только по второму закону Кирхгофа (порядок системы равен
В этой системе
В обозначениях (1.2): Рисунок 1.2 – Пример использования метода контурных токов
Метод узловых напряжений (узловых потенциалов). Этот метод позволяет уменьшить количество уравнений системы, составляемой по законам Кирхгофа, до
где
Методом узловых напряжений рекомендуется пользоваться в тех случаях, когда у < к. Сущность метода состоит в определении напряжений (потенциалов) всех узлов схемы относительно одного из них (базисного), выбранного произвольно. Потенциал базисного узла принимается нулевым. Условно за положительное направление узловых потенциалов принимают направление от данного узла к базисному. Для нахождения узловых напряжений
Суммирование в правых частях (1.3) распространяется на все ветви, присоединённые к
После нахождения потенциалов
где Пример использования МУН представлен на рисунке 1.3.
Рисунок 1.3 - Пример использования метода узловых напряжений
Описание установки Экспериментальная часть работы выполняется на одном из модулей стенда ЛСЭ-2, содержащем два источника э.д.с. В п. 4.2 (см. далее) не для всех вариантов заданий возможно использование источников э.д.с. данного модуля. В этих случаях в качестве
Рисунок 1.4 – Схема экспериментальной цепи
Программа работы 4.1 Получить у преподавателя вариант задания по входным зажимам схемы (таблица 1.1), а также комплект монтажных проводов. Рассчитать методом свёртки сопротивление схемы относительно этих зажимов. Все другие зажимы схемы рисунка 1.4 попарно закоротить, т.е. соединить монтажными проводами, собрав при этом соответствующую цепь на стенде. 4.2 Подключить к заданным входным зажимам полученной цепи один из источников э.д.с. Причём, для вариантов 1 - 4 следует брать источник
где
Расчётную или экспериментальную схему занести в отчёт.
Таблица 1.1 – Варианты заданий
4.3 Экспериментально определить токи во всех ветвях цепи при включении между зажимами 4.4 Исследованную в п. 4.3 цепь рассчитать при помощи МКТ. Результаты расчёта 4.5 Определить погрешность
и занести ее в таблицу 1.2. В (1.6)
Таблица 1.2 – Результаты эксперимента и расчёта
4.6*) Произвести расчёт исследованной в п. 4.3 цепи методом узловых напряжений. Результаты расчёта 4.7*) Определить погрешность 4.8 Сделать выводы по работе.
5 Контрольные вопросы 1. Что физически выражают 1-й и 2-й законы Кирхгофа? 2. Каковы отличительные признаки простых цепей? 3. В чём сущность метода свёртки схемы? 4. Каково главное условие эквивалентного преобразования схем? 5. В чём достоинство МКТ по сравнению с методом составления полной системы уравнений Кирхгофа? 6. Каков общий порядок применения МКТ для расчёта схем? 7. Чем определяется количество уравнений, записываемых по МКТ? ______________________________________________________________________________________________________________________________________________________________________________________ *) только для студентов специальностей 150200, 181300, 190100, 190600, 200800, 220500. 8. Возможно ли измерение контурного тока или же это исключительно расчётная абстракция? 9. Что такое собственное и общее (взаимное) сопротивление? 10. Как на основе контурных токов определяются токи реальные?
Дополнительные вопросы для студентов специальностей 150200, 181300, 190100, 190600, 200800, 220500: 11. В чём достоинство МУН по сравнению с методом составления полной системы уравнений Кирхгофа? 12. Возможно ли преимущество МУН перед МКТ? 13. Каков общий порядок использования МУН для расчёта схем? 14. Каково правило знаков в МУН? 15. Чем определяется количество уравнений, записываемых по МУН? 16. Можно ли записывать уравнение для опорного узла? Каковы критерии выбора опорного узла?
17. Что такое собственная и взаимная (общая) проводимость?
Литература 1. Теоретические основы электротехники. Т.1. Основы теории 2. Касаткин А.С., Немцов М.В. Электротехника. М.: ЭАИ, 1983. - 3. Матханов П.Н. Основы анализа электрических цепей. Линей- 4. Иванов А.А. Электротехника. Лабораторные работы. - Киев: 5. Попов В.П. Основы теории цепей: Учебник для вузов.- 2-е изд.
ЛАБОРАТОРНАЯ РАБОТА № 2
ЛИНЕЙНАЯ НЕРАЗВЕТВЛЁННАЯ ЦЕПЬ Цель работы 1.1 Исследовать электрическое состояние линейной неразветвлённой цепи синусоидального тока при различных параметрах реактивных элементов. 1.2 Убедиться в наличии сопротивлений у индуктивного и ёмкостного элементов при протекании через них переменного тока. 1.3 Освоить метод представления синусоидальных величин векторами и метод построения векторных диаграмм напряжения. 1.4 Убедиться в возможности возникновения резонанса напряжения. Определить условия его возникновения. Порядок выполнения работы 4.1 Собрать схему согласно рисунку 2.3. Предъявить ее для проверки лаборанту или преподавателю. Установить сердечник в катушку. 4.2 Установить ручку ЛАТРа в положение «0» и включить тумблер 4.3 Установить ёмкость конденсаторной батареи 14 … 16 мкФ и поднять напряжение на входе цепи до значения, обеспечивающего ток в цепи 0,6 … 0,7 А. Не изменяя далее получившееся напряжение, откорректировать ёмкость батареи конденсаторов таким образом, чтобы ток в цепи стал максимальным. 4.4 Зафиксировать во второй строке таблицы 2.1 установленную ёмкость конденсаторной батареи - 4.5 Снизить ёмкость конденсаторной батареи примерно в два раза по сравнению с ёмкостью, полученной в п.п. 4.4, и зафиксировать данные тех же приборов в первой строке таблицы 2.1. 4.6 Увеличить ёмкость конденсаторной батареи примерно в два раза по сравнению с ёмкостью, полученной в п.п. 4.4, и зафиксировать данные тех же приборов в третьей строке таблицы 2.1. 4.7 Снизить напряжение
Обработка результатов
Таблица 2.1 – Экспериментальные данные
Таблица 2.2 – Расчетные данные
5.1 По данным измерений методом засечек построить три векторные диаграммы напряжений. Построение выполнить в масштабе
5.2 Из векторных диаграмм (рисунок 2.2б) получить проекции 5.3 Построенные векторные диаграммы предъявить преподавателю. 5.4 Произвести расчет указанных в таблице 2.2 величин по формулам (2.3) … (2.10), (2.13). Графа «характер цепи» заполняется на основе сопоставления значений 5.5 Определить для момента резонанса значения добротности
Значения 5.6 Сделать выводы.
6 Контрольные вопросы 1. Каково соответствие синусоидальной величины, например тока, и изображающего его вектора? 2. Каковы основные особенности функционирования неразветвлённой цепи при питании синусоидальным напряжением или током по сравнению с питанием постоянным выражением или током? 3. Как отличаются режимы работы цепи при различных соотношениях параметров реактивных элементов? 4. Как экспериментально определяются активное и реактивное сопротивления катушки индуктивности? 5. Изменяется ли активная составляющая полного напряжения цепи при изменении ёмкости? 6. Почему момент резонанса напряжений регистрируется по максимальному току цепи? 7. Активное сопротивление идеальной катушки индуктивности отсутствует. Каким будет резонансное сопротивление цепи при соединении такой катушки последовательно с конденсатором необходимой емкости? 8. В работе резонанс напряжений достигался изменением ёмкости конденсаторной батареи. Имеются ли другие возможности достижения резонанса? 9. Всегда ли в момент резонанса напряжений на реактивных элементах цепи больше полного напряжения цепи? 10. Каково практическое значение резонанса напряжений? Дополнительные вопросы для студентов специальностей 150200, 181300, 190100, 190600, 200800, 220500: 11. В чём заключается информационная ценность векторных диаграмм? 12. Всегда ли резонанс напряжений представляет опасность для элементов неразветвлённой цепи? 13. Можно ли по данным таблицы 2.2 построить частотные характеристики цепи? 14. Записать комплекс полного сопротивления цепи для первой строки таблицы 2.2. 15. Влияет ли величина активного сопротивления катушки на резонансную частоту последовательной цепи? 16. В чём состоит достоинство высокодобротной резонансной цепи? 17. Потребляет ли цепь реактивную мощность в момент резонанса? 18. По любой из построенных векторных диаграмм записать приложенное к цепи напряжение в виде комплексной величины (в алгебраической или показательной форме) и в виде синусоидальной величины.
Литература 1. Иванов А.А. Электротехника. Лабораторные работы.- Киев: Вища шк., 1976. – С. 53-60. 2. Касаткин А.С., Немцов М.В. Электротехника. – М.: Энергоатомиздат, 1983. – С. 57-78. 3. Теоретические основы электротехники. Т. I. Основы теории линейных цепей. Под ред. П.А. Ионкина. – М.: Высш. шк., 1976. – 4. Матханов П.Н. Основы анализа электрических цепей. Линейные цепи. – М.: Высш.шк., 1990. – С. 181-187, 190-195. 5. Попов В.П. Основы теории цепей: Учебн. для вузов. – 2-е изд. – М: Высш.шк., 1998. – С. 65-105, 108-116, 175-184.
ЛАБОРАТОРНАЯ РАБОТА № 3 Цели работы 1.1 Исследовать электрическое состояние линейной разветвлённой цепи синусоидального тока при различных параметрах реактивных элементов. 1.2 По опытным данным построить векторные диаграммы токов, убедиться в возможности установления резонанса токов и определить условия его возникновения.
Порядок выполнения работ 4.1 Собрать схему согласно рисунку 3.3. Предъявить ее для проверки преподавателю или лаборанту. Установить сердечник в катушку. 4.2 Повернуть ручку ЛАТРа в положение «0» и включить тумблер 4.3 Установить ёмкость конденсаторной батареи С =16… 4.4 Зафиксировать в таблице 3.1 величину ёмкости 4.5 Уменьшать ёмкость 4.6 Уменьшить ёмкость 4.7 Снизить напряжение
Обработка результатов
Таблица 3.1 – Экспериментальные данные
5.1 По данным измерений построить три векторные диаграммы токов, пользуясь уравнением (3.8) и методом засечек. Построение векторных диаграмм выполнить в масштабе 5.2 Из векторных диаграмм (рисунок 3.2) получить проекции
Таблица 3.2 – Расчетные данные
____________________________________________________________________________________________________ *) Если ток 5.3 Построенные векторные диаграммы предъявить преподавателю. 5.4 Произвести расчёт указанных в таблице 3.2 величин по формулам (3.2) … (3.7), (3.12), (3.13), занести значения в таблицу 3.2. Графа «Характер цепи» заполняется на основе сопоставления значений 5.5 Определить для момента резонанса значения волнового сопротивления 5.6 Сделать выводы по работе.
6 Контрольные вопросы 1. Каковы основные особенности функционирования разветвлённой цепи при питании её синусоидальным напряжением или током по сравнению с питанием постоянным напряжением или током? 2. Как отличаются режимы работы цепи при различных соотношениях параметров пассивных элементов? 3. Как определить активное и реактивное сопротивление катушки индуктивности? 4. Изменяется ли активная составляющая полного тока цепи при изменении ёмкости? 5. Почему момент резонанса регистрируется по минимальному полному току цепи? 6. Активное сопротивление идеальной катушки индуктивности отсутствует. Каким будет резонансное сопротивление цепи при включении такой катушки параллельно конденсатору? 7. При каких условиях полный ток цепи становится меньше тока в отдельных ветвях? 8. В работе резонанс токов достигался изменением ёмкости конденсаторов. Имеются ли другие возможности достижения резонанса? 9. Для чего и как производится компенсация индуктивного тока? 10. В чём недостаток перекомпенсации?
Дополнительные задания и вопросы для студентов специальностей 150200, 181300, 190100, 190600, 200800, 220500:
11. Получить значение полной, активной и реактивной мощности по одной из векторных диаграмм. 12. При каких условиях в параллельно соединённых реактивных элементах резонанс токов не возникает? 13. В чем достоинство высокодобротных резонансных
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 535; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.219.221 (0.017 с.) |






 в-1
в-1

 в-2
в-2
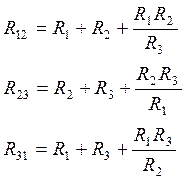

 (1.1)
(1.1) число ветвей цепи;
число ветвей цепи; число узлов цепи;
число узлов цепи; число источников тока цепи.
число источников тока цепи. (формула (1.1)). Причём, из пути их протекания следует исключить ветви с источниками тока.
(формула (1.1)). Причём, из пути их протекания следует исключить ветви с источниками тока.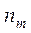 контурных токов следует направить так, чтобы каждый из них проходил через один источник тока. При таком выборе можно считать эти
контурных токов следует направить так, чтобы каждый из них проходил через один источник тока. При таком выборе можно считать эти  контурных токов известными, задаваемыми условиями задачи:
контурных токов известными, задаваемыми условиями задачи: 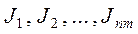 .
. ):
):
 собственное сопротивление контура. Оно равно сумме сопротивлений ветвей, входящих в этот контур. Падение напряжения на этих сопротивлениях всегда положительно.
собственное сопротивление контура. Оно равно сумме сопротивлений ветвей, входящих в этот контур. Падение напряжения на этих сопротивлениях всегда положительно. сопротивления ветви, общей для
сопротивления ветви, общей для  -го и
-го и  -го контуров. При согласном протекании токов
-го контуров. При согласном протекании токов  и
и  по этой ветви падение напряжения берется со знаком «+», при встречном – со знаком «–». Сопротивления, фигурирующие под знаком суммирования в правой части (1.2), – это сопротивления ветвей, общих для рассматриваемого контура и контура, по которому протекает известный контурный ток, задаваемый соответствующим источником тока. Правило знаков для падения напряжений в этих случаях – обратное.
по этой ветви падение напряжения берется со знаком «+», при встречном – со знаком «–». Сопротивления, фигурирующие под знаком суммирования в правой части (1.2), – это сопротивления ветвей, общих для рассматриваемого контура и контура, по которому протекает известный контурный ток, задаваемый соответствующим источником тока. Правило знаков для падения напряжений в этих случаях – обратное.  алгебраическая сумма э.д.с., действующих в рассматриваемом контуре. После расчёта системы (1.2) относительно контурных токов
алгебраическая сумма э.д.с., действующих в рассматриваемом контуре. После расчёта системы (1.2) относительно контурных токов 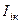 реальные токи определяются алгебраической суммой контурных токов, протекающих в данной ветви. На рисунке 1.2 представлен пример использования метода контурных токов.
реальные токи определяются алгебраической суммой контурных токов, протекающих в данной ветви. На рисунке 1.2 представлен пример использования метода контурных токов.

 неизвестны
неизвестны
 известен
Система:
известен
Система:
 Токи в ветвях:
Токи в ветвях:
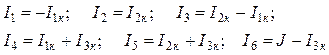


 ,
, число ветвей, содержащих только идеальные источники
число ветвей, содержащих только идеальные источники  составляется и решается следующая система, основанная на первом законе Кирхгофа:
составляется и решается следующая система, основанная на первом законе Кирхгофа:
 -му узлу. В этой системе каждое уравнение соответствует отдельному узлу.
-му узлу. В этой системе каждое уравнение соответствует отдельному узлу.  сумма проводимости ветвей, присоединённых к узлу «
сумма проводимости ветвей, присоединённых к узлу « » (собственная проводимость узла).
» (собственная проводимость узла).  сумма проводимости ветвей, включённых между узлами «
сумма проводимости ветвей, включённых между узлами « » и «
» и « » (взаимная проводимость узла).
» (взаимная проводимость узла).  алгебраическая сумма произведений э.д.с. на проводимости ветвей, подключённых к узлу «
алгебраическая сумма произведений э.д.с. на проводимости ветвей, подключённых к узлу « ».
».  алгебраическая сумма источников тока, присоединённых к узлу «
алгебраическая сумма источников тока, присоединённых к узлу « ».
». ток в ветви, включённой между узлами «
ток в ветви, включённой между узлами « » и «
» и « », можно найти по формуле:
», можно найти по формуле:
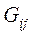 и
и  это (в отличие от (1.3)) величины, относящиеся к от-
это (в отличие от (1.3)) величины, относящиеся к от-
 неизвестные
Узел «0» – опорный.
неизвестные
Узел «0» – опорный.  Система:
Система:


 и
и 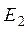 , резисторы различных номиналов
, резисторы различных номиналов  , разъёмы
, разъёмы  , переключатели
, переключатели  , а также измерительные приборы
, а также измерительные приборы  и
и  . Всё это смонтировано в центральной части модуля в цепь, схема которой представлена на рисунке 1.4. Слева от цепи размещён многопредельный вольтметр PV, справа – многопредельный миллиамперметр PA. Источники э.д.с.
. Всё это смонтировано в центральной части модуля в цепь, схема которой представлена на рисунке 1.4. Слева от цепи размещён многопредельный вольтметр PV, справа – многопредельный миллиамперметр PA. Источники э.д.с.  и
и  являются регулируемыми в пределах 0 … 12 В. Ручки регулировки выведены на лицевую панель модуля.
являются регулируемыми в пределах 0 … 12 В. Ручки регулировки выведены на лицевую панель модуля.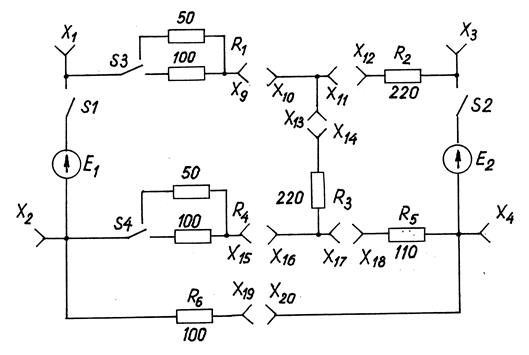
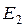 при этом выключен, а зажимы
при этом выключен, а зажимы 
 закорочены). Для вариантов 5 - 8 следует брать источник
закорочены). Для вариантов 5 - 8 следует брать источник  при этом выключен, зажимы
при этом выключен, зажимы  закорочены). Для остальных вариантов оба источника модуля должны быть отключены, зажимы
закорочены). Для остальных вариантов оба источника модуля должны быть отключены, зажимы  попарно закорочены, а в качестве источника выбирается любой из регулируемых источников напряжения постоянного тока, имеющихся на стенде ЛСЭ-2. Пользуясь методом амперметра и вольтметра и применяя при этом упомянутые приборы
попарно закорочены, а в качестве источника выбирается любой из регулируемых источников напряжения постоянного тока, имеющихся на стенде ЛСЭ-2. Пользуясь методом амперметра и вольтметра и применяя при этом упомянутые приборы  и
и  модуля, экспериментально определить сопротивление цепи на трёх значениях напряжения источника. Усреднить полученный результат и сопоставить его с данными расчёта п. 4.1. Определить погрешность:
модуля, экспериментально определить сопротивление цепи на трёх значениях напряжения источника. Усреднить полученный результат и сопоставить его с данными расчёта п. 4.1. Определить погрешность: (1.5)
(1.5) экспериментально определённое сопротивление цепи
экспериментально определённое сопротивление цепи  то же, полученное расчётным путём (п. 4.1.);
то же, полученное расчётным путём (п. 4.1.); .
. ,
Ом
,
Ом
 ,
Ом
,
Ом
 источника э.д.с.
источника э.д.с.  , а между зажимами
, а между зажимами 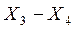 источника э.д.с.
источника э.д.с.  получить у преподавателя. Значения токов
получить у преподавателя. Значения токов  вписать в таблицу 1.2. Схему занести в отчёт.
вписать в таблицу 1.2. Схему занести в отчёт. занести в таблицу 1.2. Расчётную систему уравнений к ней поместить в отчёт.
занести в таблицу 1.2. Расчётную систему уравнений к ней поместить в отчёт. (1.6)
(1.6)
 , мА
, мА
 , мА
, мА
 , %
, %
 , мА *)
, мА *)
 , % *)
, % *)
 вписать в таблицу 1.2. Расчётную схему занести в отчёт.
вписать в таблицу 1.2. Расчётную схему занести в отчёт. данного расчёта с экспериментом по формуле, аналогичной (1.6). Результаты занести в таблицу 1.2.
данного расчёта с экспериментом по формуле, аналогичной (1.6). Результаты занести в таблицу 1.2. .
. , показания приборов:
, показания приборов:  - напряжение
- напряжение  ;
;  - ток
- ток  ;
;  при подключении к зажимам
при подключении к зажимам  - напряжение
- напряжение 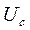 ;
; 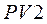 при подключении к зажимам
при подключении к зажимам  - напряжение
- напряжение  .
. до нуля, отключить тумблер
до нуля, отключить тумблер  . Полученные данные предъявить преподавателю для проверки.
. Полученные данные предъявить преподавателю для проверки.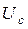 , В
, В
 , В
, В
 В/см (или
В/см (или  , или
, или  ), где
), где
 напряжения
напряжения  на вектор тока
на вектор тока  и угол сдвига по фазе
и угол сдвига по фазе  между полным током
между полным током  и напряжением
и напряжением  . Полученные данные занести в соответствующие графы таблицы 2.2.
. Полученные данные занести в соответствующие графы таблицы 2.2. и
и 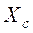 .
. по формуле (2.19),
по формуле (2.19),  - по формуле (2.18) и расхождение
- по формуле (2.18) и расхождение %,
%, .
. и
и  брать из таблицы 2.2 соответствующие резонансу напряжений.
брать из таблицы 2.2 соответствующие резонансу напряжений. .
. установить в положение «2» - для измерения тока
установить в положение «2» - для измерения тока  . Поднимать с помощью ЛАТРа напряжение
. Поднимать с помощью ЛАТРа напряжение 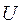 до тех пор, пока амперметр не покажет максимальный ток (1А) или несколько меньше.
до тех пор, пока амперметр не покажет максимальный ток (1А) или несколько меньше. , установленное напряжение
, установленное напряжение  , ток конденсаторной батареи
, ток конденсаторной батареи  . Переключателем
. Переключателем  в положении «1» и «3» зарегистрировать токи в катушке
в положении «1» и «3» зарегистрировать токи в катушке  и полный ток
и полный ток  и занести эти данные в таблицу 3.1.
и занести эти данные в таблицу 3.1. конденсаторной батареи до тех пор, пока ток I (переключатель
конденсаторной батареи до тех пор, пока ток I (переключатель 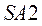 - в положении «3») не достигнет минимального значения. Напряжение при этом не изменять. Зарегистрировать величину полученной ёмкости, полный ток и токи в ветвях, внести их в таблицу 3.1.
- в положении «3») не достигнет минимального значения. Напряжение при этом не изменять. Зарегистрировать величину полученной ёмкости, полный ток и токи в ветвях, внести их в таблицу 3.1. конденсаторной батареи еще на 30 … 40% по сравнению с предыдущим опытом и, оставив напряжение без изменений, зафиксировать полученные данные в таблице 3.1.*)
конденсаторной батареи еще на 30 … 40% по сравнению с предыдущим опытом и, оставив напряжение без изменений, зафиксировать полученные данные в таблице 3.1.*) . Сердечник катушки сразу не вытаскивать (он может быть очень горячим). Полученные данные показать преподавателю.
. Сердечник катушки сразу не вытаскивать (он может быть очень горячим). Полученные данные показать преподавателю. , мкФ
, мкФ
 , В
, В
 , А
, А
 , А
, А
 А/см (или
А/см (или  А/см, или
А/см, или  А/см), где
А/см), где 
 тока
тока  на вектор напряжения
на вектор напряжения  и угол сдвига по фазе
и угол сдвига по фазе  между полным током
между полным током  № п/п
№ п/п
 при этом меньше 0,3 А, его измерение произвести переносным амперметром (с пределом до 300 мА), получив его у лаборанта или преподавателя.
при этом меньше 0,3 А, его измерение произвести переносным амперметром (с пределом до 300 мА), получив его у лаборанта или преподавателя. и вспомогательной величины
и вспомогательной величины  .
. и расхождение
и расхождение  . Значение
. Значение  брать соответствующее резонансу токов, а
брать соответствующее резонансу токов, а 



