
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейная разветвлённая цепь синусоидального токаСодержание книги
Поиск на нашем сайте
Цели работы 1.1 Исследовать электрическое состояние линейной разветвлённой цепи синусоидального тока при различных параметрах реактивных элементов. 1.2 По опытным данным построить векторные диаграммы токов, убедиться в возможности установления резонанса токов и определить условия его возникновения.
Основные теоретические положения Существует несколько способов анализа линейной разветвлённой цепи синусоидального тока (рисунок 3.1).
Это позволяет считать, что активное сопротивление конденсатора не влияет на анализ схемы. В то же время активное сопротивление используемых катушек индуктивности сопротивление конденсатора
ёмкость конденсатора
модуль полного сопротивления катушки
активное сопротивление катушки
реактивное сопротивление катушки
индуктивность катушки
В формулах (3.3) и (3.7) предполагается, что частота приложенного напряжения
из векторного уравнения по первому закону Кирхгофа:
Из векторной диаграммы видно, что в данном режиме реактивная составляющая полного тока
отрицательна. Следовательно, угол сдвига фаз
также отрицательный; б) в)
где
Из формулы (3.13) видно, что: 1. Резонанс токов возможен не при любом сочетании параметров
2. Значение резонансной частоты зависит от величины активного сопротивления катушки индуктивности. Эти две особенности отличают резонанс токов от резонанса напряжений. В момент резонанса
при постоянстве амплитуды приложенного напряжения будет иметь минимальное значение
Минимум полного тока цепи является экспериментальным признаком резонанса тока. В ветвях с реактивными элементами токи больше полного тока, по крайней мере, в
Сопоставление формул (3.11) и (3.16) позволяет заключить, что в момент резонанса
или после некоторых преобразований
где В силовой электротехнике ёмкость требуемого для резонанса конденсатора получается значительной, поэтому полного резонанса ( Ёмкость конденсаторов при этом определяют по несколько изменённой формуле (3.18):
В электронике, радиотехнике резонанс токов в высокодобротных (
|
|||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 210; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.181.181 (0.009 с.) |

 Рисунок 3.1 - Исходная схема
Рисунок 3.1 - Исходная схема
 активной и
активной и  реактивной, т.е.
реактивной, т.е.
 (3.1)
Используемые в лабораторном стенде конденсаторы близки по своим свойствам к идеальным, т.е. можно считать, что
(3.1)
Используемые в лабораторном стенде конденсаторы близки по своим свойствам к идеальным, т.е. можно считать, что  , значит
, значит  .
.
 составляет заметную величину, и им пренебречь нельзя. Таким образом, в токе с катушкой
составляет заметную величину, и им пренебречь нельзя. Таким образом, в токе с катушкой 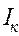 будут обе составляющие – и активная
будут обе составляющие – и активная  , и реактивная
, и реактивная 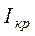 . Зная эти токи, например, определив экспериментально (токи
. Зная эти токи, например, определив экспериментально (токи  ) или построением векторных диаграмм (токи
) или построением векторных диаграмм (токи  рисунок 3.2), можно определить параметры пассивных элементов схемы (рисунок 3.1) по следующим формулам:
рисунок 3.2), можно определить параметры пассивных элементов схемы (рисунок 3.1) по следующим формулам: (3.2)
(3.2) мкФ; (3.3)
мкФ; (3.3) (3.4)
(3.4) (3.5)
(3.5) (3.6)
(3.6) (3.7)
(3.7) Гц. В зависимости от соотношения параметров реактивных элементов цепь на рисунке 3.1 может находиться в трёх режимах:
Гц. В зависимости от соотношения параметров реактивных элементов цепь на рисунке 3.1 может находиться в трёх режимах: Рисунок 3.2 – Векторная диаграмма токов
Рисунок 3.2 – Векторная диаграмма токов
 перекомпенсация. В данном режиме цепь имеет активно-емкостный характер. Этому режиму соответствует следующее соотношение реактивных составляющих токов:
перекомпенсация. В данном режиме цепь имеет активно-емкостный характер. Этому режиму соответствует следующее соотношение реактивных составляющих токов:
 Для этого режима на рисун-ке 3.2 методом засечек построена векторная диаграмма, исходящая
Для этого режима на рисун-ке 3.2 методом засечек построена векторная диаграмма, исходящая
 . (3.8)
. (3.8)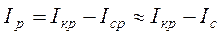 (3.9)
(3.9) между полным током
между полным током  и напряжением
и напряжением  цепи
цепи (3.10)
(3.10)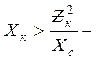 недокомпенсация; в этом режиме цепь имеет активно-индуктивный характер,
недокомпенсация; в этом режиме цепь имеет активно-индуктивный характер,  ;
; полная компенсация или резонанс токов, при этом цепь в целом имеет характер активного сопротивления
полная компенсация или резонанс токов, при этом цепь в целом имеет характер активного сопротивления 
 (3.11)
(3.11) – (3.12)
– (3.12) резонансная частота, определяемая по формуле:
резонансная частота, определяемая по формуле: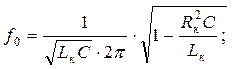 (3.13)
(3.13)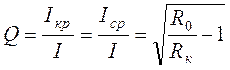 – добротность резонансной цепи. (3.14)
– добротность резонансной цепи. (3.14)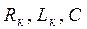 , а лишь при
, а лишь при или
или 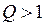 .
. , т.е. напряжение и полный ток цепи совпадают по фазе. Кроме того, полный ток цепи
, т.е. напряжение и полный ток цепи совпадают по фазе. Кроме того, полный ток цепи (3.15)
(3.15)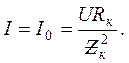 (3.16)
(3.16) раз:
раз:
 , а это равенство дает возможность подобрать ёмкость конденсатора
, а это равенство дает возможность подобрать ёмкость конденсатора  , необходимую для установления резонанса – при известных параметрах катушки индуктивности
, необходимую для установления резонанса – при известных параметрах катушки индуктивности  и частоте
и частоте  приложенного напряжения, – по формуле
приложенного напряжения, – по формуле (3.17)
(3.17) (3.18)
(3.18) мощность ветви катушки,
мощность ветви катушки, 
 ) не добиваются. Ограничиваются достижением режимов, близких к резонансным с
) не добиваются. Ограничиваются достижением режимов, близких к резонансным с 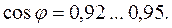
 . (3.19)
. (3.19) ) цепях используется для фильтрации и выделения сигналов определённой частоты.
) цепях используется для фильтрации и выделения сигналов определённой частоты.


