
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гідравлічні втрати тиску при ламінарному русі в’язкопластичної рідини у концентричному кільцевому просторіСодержание книги
Поиск на нашем сайте
Знайдемо зв'язок між перепадом тиску
При русі в`язкопластичної рідини у концентричному кільцевому просторі утворюється ядро, яке має форму пустотілого циліндра з площею поперечного перерізу
Рисунок 2.8 – Схема розподілення швидкостей і напружень при ламінарній течії ВПР у кільцевому каналі
Це ядро розділяє потік на два градієнтних шари. У першому шарі (I) похідна При знаходженні профілю швидкостей Рівняння руху:
Рівняння збереження маси:
Рівняння стану:
Реологічне рівняння стану:
де Реологічне рівняння для першого шару:
Реологічне рівняння для другого шару:
Умова рівноваги сил, які діють на ядро записується таким чином:
Граничні умови при відсутності ковзання:
Оскільки ядро рухається з постійною швидкістю
Крім того, повинна виконуватися умова:
Рівняння (2.63) з врахуванням (2.64) буде мати вигляд
Рівняння (2.64) показує, що при осесиметричному усталеному русі швидкість
Інтегруючи перше співвідношення (2.74) з врахуванням (2.75)
одержимо:
де Підставляючи реологічні рівняння (2.67) і (2.68) у друге співвідношення (2.74) та інтегруючи для кожного градієнтного шару одержимо: для першого шару (
для другого шару (
Невідомі постійні

Невідомі із системи (2.79) в явному вигляді не знаходять із-за їх наявності в рівняннях як під знаком логарифма, так і у вигляді одночленів, тобто внаслідок трансцендентності системи. Тому вважаючи постійні
Де величина А згідно з рівняннями (2.74) і (2.76) дорівнює
Систему рівнянь (2.79) і (2.80) можна звести до двох рівнянь. Інтегрування і виключення невідомих
де "
Ці два рівняння (2.82) і (2.83) перетворюються у вигляд:
де
де
За рівнянням (2.84) з урахуванням залежності (2.85) можна побудувати графік: На рисунку 2.7 приведена лише одна усереднена крива 2 для діапазону d, який найчастіше трапляється у практиці. Таким чином, за допомогою рівняння (2.87) можна знайти перепад тиску в кільцевому просторі за формулою:
Попередньо за кривою 2 рисунок 2.7 знаходять коефіцієнт " Графічний метод розрахунку втрат тиску при ламінарному русі в`язкопластичних рідин у трубах і кільцевому просторі розроблений К.Х. Гродде. Цей метод зручний і його точність визначається похибкою знаходження величини Гідравлічні втрати тиску в концентричному кільцевому просторі при ламінарному русі в’язкопластичної рідини наближено можна знайти за формулою, яка базується на принципі адитивності в’язкої і пластичної компонент тиску Для в’язкопластичної рідини можна застосовувати таку формулу для визначення втрат тиску в кільцевому просторі при ламінарному режимі руху:
де
|
||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 179; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.21.106 (0.007 с.) |

 і витратою
і витратою  , де
, де  - середня швидкість у кільцевому просторі з площею перерізу
- середня швидкість у кільцевому просторі з площею перерізу .
. , боковою поверхнею
, боковою поверхнею  , і рухається зі швидкістю
, і рухається зі швидкістю 
 , а у другому шарі (II)
, а у другому шарі (II)  .
. . (2.63)
. (2.63) . (2.64)
. (2.64) . (2.65)
. (2.65) . (2.66)
. (2.66)
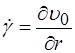 .
.
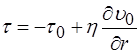 . (2.67)
. (2.67)
 . (2.68)
. (2.68) ,
,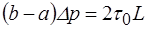 . (2.69)
. (2.69) . (2.70)
. (2.70) при
при  . (2.71)
. (2.71) при
при  . (2.72)
. (2.72)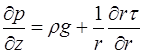 . (2.73)
. (2.73) є тільки функція радіуса
є тільки функція радіуса  і таким чином з (2.73) виходить, що
і таким чином з (2.73) виходить, що  є функція радіуса
є функція радіуса  , оскільки тиск є функцією
, оскільки тиск є функцією  , тобто знайдемо значення
, тобто знайдемо значення  , обумовлене силами тертя. Таким чином
, обумовлене силами тертя. Таким чином і
і  . (2.74)
. (2.74) , (2.75)
, (2.75) , (2.76)
, (2.76) ,
,  .
. . (2.77)
. (2.77)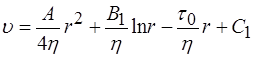 . (2.78)
. (2.78) , а також розміри ядра
, а також розміри ядра  і швидкість
і швидкість  (2.80)
(2.80) . (2.81)
. (2.81) із рівнянь (2.80) і (2.79) дає формулу:
із рівнянь (2.80) і (2.79) дає формулу: (2.82)
(2.82) " знаходять із рівняння Воларовича–Гуткіна:
" знаходять із рівняння Воларовича–Гуткіна: (2.83)
(2.83) (2.84)
(2.84) . (2.85)
. (2.85)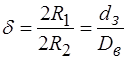 - відношення зовнішнього діаметра внутрішньої труби
- відношення зовнішнього діаметра внутрішньої труби 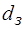 до внутрішнього діаметра зовнішньої труби
до внутрішнього діаметра зовнішньої труби  ;
; відношення подвоєної віддалі, яку відраховують від осі труби до зовнішньої межі ядра кільцевого потоку, до внутрішнього діаметра зовнішньої труби, причому:
відношення подвоєної віддалі, яку відраховують від осі труби до зовнішньої межі ядра кільцевого потоку, до внутрішнього діаметра зовнішньої труби, причому: ;
; - параметр Сен – Венана,
- параметр Сен – Венана,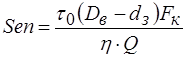 , (2.86)
, (2.86) - площа кільцевого перерізу
- площа кільцевого перерізу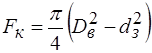 ,
, . (2.87)
. (2.87) .
. . (2.88)
. (2.88)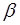 ". Для цього визначають параметр Сен–Венана за відомою витратою
". Для цього визначають параметр Сен–Венана за відомою витратою  , реологічними характеристиками
, реологічними характеристиками  та
та  і геометричними даними
і геометричними даними  .
. , (2.89)
, (2.89) - внутрішній діаметр кільця;
- внутрішній діаметр кільця; - зовнішній діаметр кільця.
- зовнішній діаметр кільця.


