
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гідравлічні втрати тиску в трубах при ламінарному русі в’язкопластичної рідиниСодержание книги
Поиск на нашем сайте
Градієнт швидкості руху рідини в трубах можна записати таким чином:
Знак "мінус" береться тому, що зі збільшенням " Слід вважати, що має місце прилипання рідини до стінки (відсутнє ковзання), а тому швидкість біля стінки
Із закону розподілу напружень:
Тоді:
Підставивши (2.33) у (2.31) одержимо:
Значить:
Вирази (2.34) і (2.35) є загальними. Їх інтегрування дозволяє встановити закон розподілу швидкостей при будь – якому значенні функції
Розв’яжемо цю задачу для руху в трубах ньютонівської рідини, для якої:
З виразу (2.32)
Підставивши (2.38) і (2.39) у рівняння (2.37) одержимо:
Рівняння виражає закон розподілу швидкостей у поперечному перерізі круглої труби при ламінарному режимі, відомий під назвою закону Стокса. Задаючись різними значеннями координати "
Середня швидкість потоку при цьому дорівнює половині осьової швидкості. При русі в’язкопластичної рідини закон розподілу швидкостей у поперечному перерізі круглої труби при ламінарному режимі буде такий:
Підставивши (2.42) у (2.35) одержимо:
Це формула для розподілу швидкостей при структурному режимі в’язко – пластичної рідини. Для визначення швидкості руху нейтрального ядра у формулу (2.43) необхідно підставити замість
При Знаючи закон розподілу швидкостей у поперечному перерізі можна вивести теоретичні формули для визначення витрати рідини і втрат тиску на тертя по довжині потоку при ламінарному режимі.
Для цього в трубі виділимо елементарний переріз у вигляді кільця внутрішнім радіусом "  " і товщиною " " і товщиною "  ", (рисунок 2.6). ", (рисунок 2.6).
 
Площа перерізу
Елементарна витрата рідини, яка проходить через кільцевий переріз:
Повна витрата рідини через весь поперечний переріз визначається як сума елементарних витрат, або те ж саме, як інтеграл, взятий по цілому перерізу, тобто в межах від Таким чином:
Інтегруючи даний вираз по частинах, знаходимо:
Перший член у правій частині рівняння дорівнює нулю, оскільки при Таким чином:
Введемо в дане рівняння нову змінну " З рівняння (2.32) маємо:
Підставивши (2.33) в (2.30) одержимо:
Підставивши у вираз (2.48) замість
Для рідин, реологічні рівняння яких допускають явний аналітичний вигляд
де
де Інтегрування даного рівняння дає можливість одержати необхідні для виконання практичних розрахунків співвідношення між витратою та перепадом тиску при будь-якому вигляді функції Для в’язкопластичної рідини (якими є промивальні рідини) формула для визначення витрати при ламінарному режимі руху може бути одержана, якщо у рівняння витрати (2.52) підставити замість функції
Проінтегруємо дане рівняння
Підставивши замість
або через діаметр труби
Цю формулу вперше одержав Е. Букінгем у 1921 році. Даний вираз в явному вигляді не розв’язується відносно
Формулу (2.55) можна привести до вигляду:
Поділимо обидві частини на
Позначивши
Побудовані графічні залежності
Рисунок 2.7 – Залежність безрозмірного коефіцієнта β від параметра Сен-Венана: 1 – для труб; 2 – для кільцевого перерізу
Із залежності
За даною формулою знаходять перепад тиску Підставивши у (2.52) замість функції
Формули (2.58) і (2.59) одержав Ж. Пуазейль у 1840 році. Підставивши у рівняння (2.52) замість функції
Формули (2.60) і (2.61) одержав В. Рабинович у 1929 році і М. Муні у 1931 році. Якщо у формулу (2.52) замість функції
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 186; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.43.106 (0.006 с.) |

 . (2.30)
. (2.30) " зменшується, тобто
" зменшується, тобто 
 величина від’ємна, а напруження "
величина від’ємна, а напруження "  " величина додатна.
" величина додатна.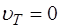 . Тоді вираз (2.30) можна записати:
. Тоді вираз (2.30) можна записати: . (2.31)
. (2.31) . (2.32)
. (2.32) . (2.33)
. (2.33) . (2.34)
. (2.34) . (2.35)
. (2.35) .
. ;
;  .
. . (2.36)
. (2.36) . (2.37)
. (2.37) (2.38)
(2.38) . (2.39)
. (2.39)
 (2.40)
(2.40) . (2.41)
. (2.41) ;
;
 ,
,  (2.42)
(2.42) .
.
 .
. ,
,  .
.

 (2.43)
(2.43) :
: (2.44)
(2.44) одержуємо формулу Стокса.
одержуємо формулу Стокса.


 . Оскільки товщина кільця безмежно мала, приймемо, що у всіх його точках швидкість частинок рідини
. Оскільки товщина кільця безмежно мала, приймемо, що у всіх його точках швидкість частинок рідини  однакова і може бути визначена рівнянням Стокса:
однакова і може бути визначена рівнянням Стокса: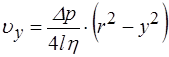 .
. . (2.45)
. (2.45) до
до  .
. . (2.46)
. (2.46) .
. . (2.47)
. (2.47) , а на осі труби
, а на осі труби  . (2.48)
. (2.48) ".
". . (2.49)
. (2.49) . (2.50)
. (2.50) та
та  їх значення з (2.49) та (2.50) одержимо:
їх значення з (2.49) та (2.50) одержимо: . (2.51)
. (2.51) ,визначення гідравлічних втрат тиску в трубах зводиться в загальному випадку до розв’язування рівняння:
,визначення гідравлічних втрат тиску в трубах зводиться в загальному випадку до розв’язування рівняння: , (2.52)
, (2.52) - витрата рідини;
- витрата рідини; - дотичне напруження зсуву на стінці труби.
- дотичне напруження зсуву на стінці труби.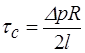 , (2.53)
, (2.53) - довжина труби.
- довжина труби. .
. ;
; ;
;  ;
; .
.
 його значення з формули (2.53) одержимо:
його значення з формули (2.53) одержимо:
 , (2.54)
, (2.54) :
: . (2.55)
. (2.55) .
.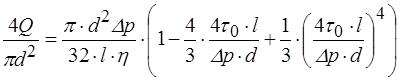 ,
,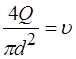 ,
, .
. :
: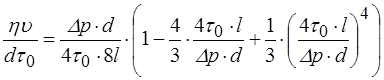 ,
, .
. ;
;  , одержимо:
, одержимо: ,
, . (2.56)
. (2.56)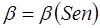 для труб і кільцевого простору, (рисунок 2.7)
для труб і кільцевого простору, (рисунок 2.7)
 одержимо:
одержимо: . (2.57)
. (2.57) реологічну модель Ньютона
реологічну модель Ньютона  одержимо формулу:
одержимо формулу: . (2.58)
. (2.58) (2.59)
(2.59) одержимо таке значення витрати і тиску при ламінарному русі рідини:
одержимо таке значення витрати і тиску при ламінарному русі рідини: . (2.60)
. (2.60) . (2.61)
. (2.61) , то одержимо таке значення витрати при ламінарному русі рідин:
, то одержимо таке значення витрати при ламінарному русі рідин: (2.62)
(2.62)


