
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основні реологічні моделі промивальних рідинСодержание книги
Поиск на нашем сайте
Для описання різноманітних технологічних процесів застосовують певні теоретичні схеми. Процеси, які відбуваються при бурінні нафтових і газових свердловин, дуже різноманітні і піддаються впливу багатьох факторів і які неможливо детально описати. Побудова моделей, які описують макропроцеси, дозволяє з достатньою для практичних цілей точністю, побудувати теорію руху промивальних рідин. Можна побудувати велику кількість моделей, які по різному моделюють процес та відображають різні його властивості. Існують різноманітні класифікації моделей. Однією з поширених класифікацій за Я. З. Ципкіним є така: а) детермінована модель; б) стохастична модель; в) адаптаційно – навчальна модель. Детермінована модель описує процеси, які визначаються початковим станом системи. Стохастична модель враховує вплив різних випадкових флуктуацій. Адаптаційно-навчальну модель застосовують у випадку, коли немає даних як з макроскопічних, так і мікроскопічних процесів, які відбуваються в системі. Моделі можуть бути фізичними і математичними. Під фізичними моделями розуміють моделі, що враховують макро- і мікроскопічні процеси, які відбуваються в системі. Математичні моделі – це те чи інше математичне описування процесів. Реологічні рівняння є математичними моделями, які відображають ідеальну поведінку реальних тіл. Реологічні рівняння для будь-якого матеріалу виражають залежність між напруженням і відповідною деформацією, тобто між кінематикою і динамікою руху частинок речовини. Релаксація – це зменшення з часом напружень при постійних деформаціях, а повзучість – це збільшення деформації з часом при постійних напруженнях. Точніше реологічні рівняння являють собою співвідношення між напруженнями
Скалярні параметри, які фігурують у даному рівнянні і характеризують реологічні властивості матеріалу, називаються реологічними константами (модулями, параметрами, коефіцієнтами), а напруження, деформації та їх похідні складають реологічні змінні. Реологічні параметри залежать як від деяких нереологічних величин (наприклад, характеристик температурного чи електромагнітного поля), так і від деяких інваріантів напружень (чи деформацій), що надає реологічному рівнянню нелінійний характер. Всі природні тіла у тій чи іншій мірі володіють трьома основними властивостями: пружністю, в’язкістю і пластичністю, на основі яких створені три базові моделі, які з достатньо високою точністю описують поведінку багатьох категорій природних матеріалів. Модель ідеально пружного середовища характеризує поведінку твердого тіла, в якого деформація зникає одночасно з напруженням. Механічна робота, яка здійснюється під дією зовнішніх навантажень, призводить до накопичення потенціальної енергії, яка при ліквідації цих навантажень повертає тілу вихідну форму і розміри. Теоретично деформація є миттєвою, тобто не залежною від часу. При незначних деформаціях залежність між напруженням і деформацією є лінійною функцією, (рисунок 2.2, а). Для простого зсуву вона описується таким рівнянням:
де
Формула (2.21) називається законом Гука і є основою лінійної теорії пружності. Модель ідеально в’язкого середовища відображає лінійне співвідношення між виникаючими в рідині напруженнями і швидкістю деформації (рисунок 2.2, б). При простому зсуві це співвідношення називають законом Ньютона:
де
Рівняння (2.22) в деякій мірі визначає текучість газів, води, нафтопродуктів та інших однофазових середовищ з низькою молекулярною масою. Швидкість деформації пропорціональна діючим напруженням, а деформація збільшується пропорціонально часу і зберігається після ліквідації напружень. Модель жорсткопластичного середовища характеризує тіло, яке не деформується до визначеного значення напруження або межі пластичності, а при перевищені його, набуває залишкової деформації, при постійному напруженні, (рисунок 2.2,в). При знятті навантаження деформація залишається і має максимальне значення, отримане під дією напруження.
а - ідеально пружного середовища; б – ідеально в’язкого середовища; в – жорсткопластичного середовища Рисунок 2.2 – Криві руху фундаментальних моделей
Співвідношення, які відображають таку поведінку при простому зсуві, мають вигляд:
де Варто зауважити, що час у даному випадку не відіграє ролі. Це і відрізняє пластичну текучість від в’язкої. Обидва види текучості зв’язані з дисипацією енергії і призводять до постійних деформацій. Якщо при в’язкій текучості енергія, затрачена на визначену деформацію, залежить від швидкості деформації, то при пластичній текучості така залежність відсутня. Три класичній моделі – тверде тіло Гука, ньютонівська рідина і тверде тіло Сен-Венана – деколи ілюструють аналогічними механічними моделями: пружною пружиною, амортизатором у вигляді ідеального поршня, який переміщується у циліндрі з в’язкою рідиною, і повзуном із сухим тертям (рисунок 2.3) Прості моделі характеризуються однією реологічною постійною.
в – тверде тіло Сен-Венана Рисунок 2.3 – Механічні аналоги складних моделей
Проте, значній категорії матеріалів властивий такий реологічний стан, який неможливо описати ні однією з основних вищенаведених моделей. Тому були створені складніші моделі з двома чи декількома реологічними постійними. Їх створення можливе двома шляхами: - аналітичним, тобто сполученням простих моделей - інтегральним, який передбачає енергетичне співвідношення між напруженнями, деформаціями і часом. Аналітичний метод передбачає послідовне чи паралельне поєднання простих моделей з метою створення складніших. Найпоширеніші дві в’язкопружні моделі і одна в’язкопластична (рисунок 2.4). В’язкопружне тіло Кельвіна–Фойхта допускає, що повне напруження містить дві складові: одна з яких створює лінійні пружні деформації, а інша – в’язкі деформації, які затримують розвиток перших. Реологічне рівняння моделі Кельвіна–Фойхта таке:
Модель характеризуються двома реологічними константами: Модель Кельвіна–Фойхта являє собою тіло із запізнілою пружністю. Її можна використовувати для описання поведінки окремих полімерів, гірських порід, а також для описання текучості бетонів, деяких розчинів, металів і т.д. В’язкопружна рідина Максвелла характеризується таким реологічним рівнянням:
Швидкість деформації має дві складові: пружну Механічним аналогом рівняння (2.25) є пристрій, який складається із послідовного з’єднаних пружини і амортизатора (рисунок 2.4, б), тобто модель Максвелла – це комбінація моделей Гука та Ньютона. З допомогою рівняння Максвелла можна описати як процес текучості, так і релаксацію напружень. Модель Максвелла характеризує рідину, яка володіє визначеною пружністю. Її можна використовувати для описання поведінки смоли, розплавленого скла, полімерних розчинів, тіста, пластичних мас та ін. В’язкопластична модель Шведова–Бінгама описує речовини, які при напруженнях, нижчих за критичне значення
Ця модель має два реологічних параметри
а – тверде тіло Кельвіна-Фойхта; б – рідина Максвелла; в – в’язкопластиче тіло Бінгама Рисунок 2.4 – Механічні аналоги складних моделей
Параметр Рідину, яка відповідає моделі Шведова–Бінгама, можна розглядати як ньютонівське середовище зі змінною в’язкістю. Всі рідини, які не підпорядковуються закону Ньютона, тобто не володіють постійною в’язкістю, називаються неньютонівськими. До рідин, поведінку яких можна описати з допомогою моделі Шведова–Бінгама, відносять суспензії (в цю категорію входить більшість промивальних рідин і тампонажних розчинів), олійні фарби, деякі мастила, фармацевтичні препарати, харчові продукти та ін.. Для описання плину рідин, які не володіють пластичними властивостями (динамічне напруження зсуву
де
При При Рівняння (2.27) описує експериментальні криві плину більшості неньютонівських непластичних рідин у діапазоні помірних швидкостей деформації. При дуже малих або дуже великих швидкостях деформації криві руху можуть бути лінеаризовані і представлені звичайним рівнянням закону Ньютона. З допомогою моделі Оствальда–де Ваале можна описати поведінку деяких емульсій, паст, продуктів харчування, фармацевтичних і біологічних препаратів, мильних речовин, клеючих речовин, полімерних розчинів, тампонажних розчинів і промивальних рідин з різними добавками. До складніших моделей (з трьома параметрами) належать модель Гершеля–Балклі, яку одержали поєднанням в’язкопластичної моделі з моделлю Оствальда–де Ваале:
Ця модель може бути використана для описання поведінки деяких бурових промивальних рідин з низьким вмістом твердої фази, оброблених полімерними розчинами. Як правило, в’язкість зменшується зі збільшенням напруження або швидкості деформації, речовини розріджуються, стають рухливішими. Це пояснюється вирівнюванням, орієнтуванням змулених несиметричних твердих частинок суспензій або розгортанням ланцюгів полімерів таким чином, щоб руху чинити мінімальний опір. Такі середовища називають псевдопластичними. Рідше трапляються рідини, в’язкість яких збільшується з підвищенням швидкості деформації. Це обумовлено руйнуванням агрегатів твердих частинок, орієнтування яких у стані спокою направлене на зменшення порожнин між ними, а також збільшенням "пористості" суспензії. Частина рідини переміщується в утворені порожнини і між частинками починає проявлятись так зване сухе тертя, змащення стає недостатнім і тертя збільшується. Такий процес відбувається в системах з високою концентрацією твердої фази і в грубих дисперсіях: водних суспензіях з високою концентрацією піску, бариту, малоколоїдної глини, слюди, металевих оксидів та ін.. Такі матеріали і речовини називають дилатантними. Деякі смоли і полімери (наприклад поліхлорвініл) проявляють псевдопластичну поведінку при малих швидкостях деформації та дилатантні при вищих швидкостях зсуву. На рисунку 2.5 показані криві руху в’язких і в’язкопластичних рідин.
1 – пружне тверде тіло; 2 – псевдопластична модель Гершеля-Балклі; 3 – модель Шведова–Бінгама; 4 – дилатантна модель Гершеля–Балклі; 5 – псевдопластична модель Освальда; 6 – модель Ньютона; 7 – дилатантна модель Освальда; 8 – ідеальна модель Рисунок 2.5 – Криві руху в’язких і в’язкопластичних рідин
У таблиці 2.2 зведені найпоширеніші реологічні моделі середовищ. Таблиця 2.2 – Реологічні моделі середовищ
У таблиці 2.2
Решта параметрів являють собою емпіричні і напівемпіричні константи. Пружні властивості не можна описати рівняннями, справедливими для простого зсуву. Ці властивості проявляються через появу напружень, перпендикулярних до напрямку руху, значення яких залежать від швидкості зсуву. Цим і відрізняється поведінка в’язкопружних середовищ від "чисто" в’язких, в яких нормальні напруження передаються з однаковою інтенсивністю у всіх напрямках у вигляді тиску. Варто зауважити, що при ламінарному русі вплив пружності незначний. Вона проявляється лише при різких змінах швидкості руху: пуск чи зупинка насосів, раптова значна зміна площі поперечного перерізу при русі через місцеві отвори і звуження (насадки, патрубки, вентилі). Наприклад, при виході із насадки, якщо вплив пружності достатньо великий, струмина не стискується, а розширюється. Особливо впливає пружність на турбулентний рух, який сприяє зменшенню тертя. Тому до промивальних рідин і тампонажних розчинів добавляють різноманітні високомолекулярні речовини для зниження як фільтрації, так і в’язкості. Відомі різні класифікації різних рідин за їх реологічною поведінкою. Одну з таких запропонував Метцнер: 1 Рідини "чисто" в’язкі (швидкість деформації залежить тільки від напружень зсуву): а) ньютонівські – в’язкість не залежить від напруження зсуву; б) неньютонівські – в’язкість є функцією напружень зсуву. 2 Рідини із залежними від часу характеристиками – швидкість деформації і в’язкість залежать як від напружень, так і від тривалості їх дії; 3 В’язкопружні рідини – швидкість деформації та в’язкість залежать від напружень та деформації зсуву. 4 Реологічно складні рідини, які мають властивості, притаманні вищеназваним категоріям. У категорію "чисто" в’язких включені і в’язкопластичні рідини. Рідини із залежними від часу характеристиками разом з в’язкопружними середовищами складають так звані "рідини з пам’яттю".
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 352; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.83.96 (0.011 с.) |

 , спричиненими деформаціями
, спричиненими деформаціями 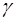 та їх похідними в часі:
та їх похідними в часі: . (2.20)
. (2.20)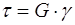 , (2.21)
, (2.21)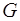 - модуль пружності при зсуві (поперечний модуль пружності або реологічна постійна тіла);
- модуль пружності при зсуві (поперечний модуль пружності або реологічна постійна тіла); , (2.22)
, (2.22) - реологічна постійна моделі або пластична в’язкість;
- реологічна постійна моделі або пластична в’язкість; швидкість деформації, спричинена дотичним напруженням
швидкість деформації, спричинена дотичним напруженням 
 (2.23)
(2.23) - реологічна константа, яка називається межею пластичності (текучості).
- реологічна константа, яка називається межею пластичності (текучості). а – тверде тіло Гука; б – ньютонівська рідина;
а – тверде тіло Гука; б – ньютонівська рідина; . (2.24)
. (2.24) . (2.25)
. (2.25) і в’язку
і в’язку  .
. (2.26)
(2.26)
 ), найчастіше використовують модель Оствальда–де Ваале з двома реологічними параметрами:
), найчастіше використовують модель Оствальда–де Ваале з двома реологічними параметрами: , (2.27)
, (2.27) і
і  - експериментальні константи;
- експериментальні константи; рівняння набуває форми закону Ньютона, при цьому
рівняння набуває форми закону Ньютона, при цьому  . Відхилення показника степеня
. Відхилення показника степеня  рідина є псевдопластична, а при
рідина є псевдопластична, а при  - дилатантна, (від латинського " dilatatio" – розширення, розтяг).
- дилатантна, (від латинського " dilatatio" – розширення, розтяг). , (2.28)
, (2.28)







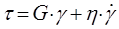

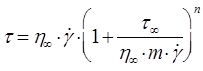


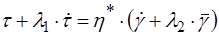

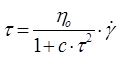

 - в’язкість при нескінченій швидкості зсуву, яка характеризує нахил лінійного відрізка кривої руху до осі абсцис при дуже високих швидкостях зсуву;
- в’язкість при нескінченій швидкості зсуву, яка характеризує нахил лінійного відрізка кривої руху до осі абсцис при дуже високих швидкостях зсуву;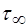 - константа, яка визначається ординатою точки перетину вказаного лінійного відрізка з віссю напружень;
- константа, яка визначається ординатою точки перетину вказаного лінійного відрізка з віссю напружень; - безрозмірна константа;
- безрозмірна константа; - уявна в’язкість при швидкостях зсуву, наближених до нуля;
- уявна в’язкість при швидкостях зсуву, наближених до нуля; , (2.29)
, (2.29) - час релаксації.
- час релаксації.


