
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Елементи гідроаеромеханіки в бурінніСодержание книги
Поиск на нашем сайте ЕЛЕМЕНТИ ГІДРОАЕРОМЕХАНІКИ В БУРІННІ Основні характеристики потоку рідини У результаті дії зовнішніх прикладених сил (сила тяжіння, тиск насосів та ін.) рідке тіло набуває усталеного або неусталеного руху. На противагу гідростатиці стан рідкого тіла, яке знаходиться в русі, визначається не тільки його тиском (гідродинамічним), але і величиною та напрямком швидкості в різних точках і в різні моменти часу. Усталеним або постійним в часі називають такий рух, при якому швидкість руху та гідродинамічний тиск в даній точці простору з часом для цієї точки не змінюються, а змінюються вони лише з переходом до іншої точки простору. При усталеному русі швидкість і гідродинамічний тиск є функціями тільки координат точки, яка рухається і аналітично може бути виражена умовою:
Із сутності усталеного руху виходить, що при даному русі через кожну визначену точку простору, заповненого рідиною, проходять безперервно частинки рідини. Елементи їх руху цілком тотожні, тому частинки переміщаються однією і тією ж траєкторією одна за одною. Усталений рух надзвичайно поширений в природі і особливо в інженерній практиці. Характерним прикладом усталеного руху є рух рідини в трубопроводі при постійній витраті, ріка, яка протікає в руслі, яке не розмивається при незмінній в часі кількості води. Неусталеним рухом називають такий рух, при якому швидкість руху і гідродинамічний тиск у кожній даній точці постійно змінюється, тобто залежить не тільки від координат точки, яка рухається, але і від часу:
Прикладом неусталеного руху є витікання із отвору резервуару, коли рівень рідини в ньому безперервно змінюється. Потік рідини, можна охарактеризувати такими параметрами: 1 Витрата 2 Живий переріз потоку 3 Змочений периметр 4 Гідравлічний радіус
5 Гідравлічний або еквівалентний діаметр
При постійній витраті
З формули (2.3) виходить, що для двох будь-яких живих перерізів
Якщо взяти ділянку між будь-якими перерізами потоку, то об’єм крапельної рідини в ньому, тобто нестискувальної рідини, не може ні збільшуватися, ні зменшуватися, оскільки це означало б зміну поперечних розмірів потоку в часі, або утворення в товщі потоку пустот, що протирічило б вимогам як усталеного руху, так і умовам суцільності. Тому завжди необхідно вважати виконанням умови:
яка називається рівнянням постійності витрати. На рисунку 2.1 і в таблиці 2.1 наведені значення живого перерізу потоку, змоченого периметра, гідравлічного радіуса, гідравлічного діаметра, площі перерізу та геометричного периметра для найпоширеніших на практиці живих перерізів.
Рисунок 2.1 – Геометричні розміри основних живих перерізів потоку
Таблиця 2.1- Основні гідравлічні елементи перерізів потоку
Рисунок 2.2 – Криві руху фундаментальних моделей
Співвідношення, які відображають таку поведінку при простому зсуві, мають вигляд:
де Варто зауважити, що час у даному випадку не відіграє ролі. Це і відрізняє пластичну текучість від в’язкої. Обидва види текучості зв’язані з дисипацією енергії і призводять до постійних деформацій. Якщо при в’язкій текучості енергія, затрачена на визначену деформацію, залежить від швидкості деформації, то при пластичній текучості така залежність відсутня. Три класичній моделі – тверде тіло Гука, ньютонівська рідина і тверде тіло Сен-Венана – деколи ілюструють аналогічними механічними моделями: пружною пружиною, амортизатором у вигляді ідеального поршня, який переміщується у циліндрі з в’язкою рідиною, і повзуном із сухим тертям (рисунок 2.3) Прості моделі характеризуються однією реологічною постійною.
в – тверде тіло Сен-Венана Рисунок 2.3 – Механічні аналоги складних моделей
Проте, значній категорії матеріалів властивий такий реологічний стан, який неможливо описати ні однією з основних вищенаведених моделей. Тому були створені складніші моделі з двома чи декількома реологічними постійними. Їх створення можливе двома шляхами: - аналітичним, тобто сполученням простих моделей - інтегральним, який передбачає енергетичне співвідношення між напруженнями, деформаціями і часом. Аналітичний метод передбачає послідовне чи паралельне поєднання простих моделей з метою створення складніших. Найпоширеніші дві в’язкопружні моделі і одна в’язкопластична (рисунок 2.4). В’язкопружне тіло Кельвіна–Фойхта допускає, що повне напруження містить дві складові: одна з яких створює лінійні пружні деформації, а інша – в’язкі деформації, які затримують розвиток перших. Реологічне рівняння моделі Кельвіна–Фойхта таке:
Модель характеризуються двома реологічними константами: Модель Кельвіна–Фойхта являє собою тіло із запізнілою пружністю. Її можна використовувати для описання поведінки окремих полімерів, гірських порід, а також для описання текучості бетонів, деяких розчинів, металів і т.д. В’язкопружна рідина Максвелла характеризується таким реологічним рівнянням:
Швидкість деформації має дві складові: пружну Механічним аналогом рівняння (2.25) є пристрій, який складається із послідовного з’єднаних пружини і амортизатора (рисунок 2.4, б), тобто модель Максвелла – це комбінація моделей Гука та Ньютона. З допомогою рівняння Максвелла можна описати як процес текучості, так і релаксацію напружень. Модель Максвелла характеризує рідину, яка володіє визначеною пружністю. Її можна використовувати для описання поведінки смоли, розплавленого скла, полімерних розчинів, тіста, пластичних мас та ін. В’язкопластична модель Шведова–Бінгама описує речовини, які при напруженнях, нижчих за критичне значення
Ця модель має два реологічних параметри
а – тверде тіло Кельвіна-Фойхта; б – рідина Максвелла; в – в’язкопластиче тіло Бінгама Рисунок 2.4 – Механічні аналоги складних моделей
Параметр Рідину, яка відповідає моделі Шведова–Бінгама, можна розглядати як ньютонівське середовище зі змінною в’язкістю. Всі рідини, які не підпорядковуються закону Ньютона, тобто не володіють постійною в’язкістю, називаються неньютонівськими. До рідин, поведінку яких можна описати з допомогою моделі Шведова–Бінгама, відносять суспензії (в цю категорію входить більшість промивальних рідин і тампонажних розчинів), олійні фарби, деякі мастила, фармацевтичні препарати, харчові продукти та ін.. Для описання плину рідин, які не володіють пластичними властивостями (динамічне напруження зсуву
де
При При Рівняння (2.27) описує експериментальні криві плину більшості неньютонівських непластичних рідин у діапазоні помірних швидкостей деформації. При дуже малих або дуже великих швидкостях деформації криві руху можуть бути лінеаризовані і представлені звичайним рівнянням закону Ньютона. З допомогою моделі Оствальда–де Ваале можна описати поведінку деяких емульсій, паст, продуктів харчування, фармацевтичних і біологічних препаратів, мильних речовин, клеючих речовин, полімерних розчинів, тампонажних розчинів і промивальних рідин з різними добавками. До складніших моделей (з трьома параметрами) належать модель Гершеля–Балклі, яку одержали поєднанням в’язкопластичної моделі з моделлю Оствальда–де Ваале:
Ця модель може бути використана для описання поведінки деяких бурових промивальних рідин з низьким вмістом твердої фази, оброблених полімерними розчинами. Як правило, в’язкість зменшується зі збільшенням напруження або швидкості деформації, речовини розріджуються, стають рухливішими. Це пояснюється вирівнюванням, орієнтуванням змулених несиметричних твердих частинок суспензій або розгортанням ланцюгів полімерів таким чином, щоб руху чинити мінімальний опір. Такі середовища називають псевдопластичними. Рідше трапляються рідини, в’язкість яких збільшується з підвищенням швидкості деформації. Це обумовлено руйнуванням агрегатів твердих частинок, орієнтування яких у стані спокою направлене на зменшення порожнин між ними, а також збільшенням "пористості" суспензії. Частина рідини переміщується в утворені порожнини і між частинками починає проявлятись так зване сухе тертя, змащення стає недостатнім і тертя збільшується. Такий процес відбувається в системах з високою концентрацією твердої фази і в грубих дисперсіях: водних суспензіях з високою концентрацією піску, бариту, малоколоїдної глини, слюди, металевих оксидів та ін.. Такі матеріали і речовини називають дилатантними. Деякі смоли і полімери (наприклад поліхлорвініл) проявляють псевдопластичну поведінку при малих швидкостях деформації та дилатантні при вищих швидкостях зсуву. На рисунку 2.5 показані криві руху в’язких і в’язкопластичних рідин.
1 – пружне тверде тіло; 2 – псевдопластична модель Гершеля-Балклі; 3 – модель Шведова–Бінгама; 4 – дилатантна модель Гершеля–Балклі; 5 – псевдопластична модель Освальда; 6 – модель Ньютона; 7 – дилатантна модель Освальда; 8 – ідеальна модель Рисунок 2.5 – Криві руху в’язких і в’язкопластичних рідин
У таблиці 2.2 зведені найпоширеніші реологічні моделі середовищ. Таблиця 2.2 – Реологічні моделі середовищ
У таблиці 2.2
Решта параметрів являють собою емпіричні і напівемпіричні константи. Пружні властивості не можна описати рівняннями, справедливими для простого зсуву. Ці властивості проявляються через появу напружень, перпендикулярних до напрямку руху, значення яких залежать від швидкості зсуву. Цим і відрізняється поведінка в’язкопружних середовищ від "чисто" в’язких, в яких нормальні напруження передаються з однаковою інтенсивністю у всіх напрямках у вигляді тиску. Варто зауважити, що при ламінарному русі вплив пружності незначний. Вона проявляється лише при різких змінах швидкості руху: пуск чи зупинка насосів, раптова значна зміна площі поперечного перерізу при русі через місцеві отвори і звуження (насадки, патрубки, вентилі). Наприклад, при виході із насадки, якщо вплив пружності достатньо великий, струмина не стискується, а розширюється. Особливо впливає пружність на турбулентний рух, який сприяє зменшенню тертя. Тому до промивальних рідин і тампонажних розчинів добавляють різноманітні високомолекулярні речовини для зниження як фільтрації, так і в’язкості. Відомі різні класифікації різних рідин за їх реологічною поведінкою. Одну з таких запропонував Метцнер: 1 Рідини "чисто" в’язкі (швидкість деформації залежить тільки від напружень зсуву): а) ньютонівські – в’язкість не залежить від напруження зсуву; б) неньютонівські – в’язкість є функцією напружень зсуву. 2 Рідини із залежними від часу характеристиками – швидкість деформації і в’язкість залежать як від напружень, так і від тривалості їх дії; 3 В’язкопружні рідини – швидкість деформації та в’язкість залежать від напружень та деформації зсуву. 4 Реологічно складні рідини, які мають властивості, притаманні вищеназваним категоріям. У категорію "чисто" в’язких включені і в’язкопластичні рідини. Рідини із залежними від часу характеристиками разом з в’язкопружними середовищами складають так звані "рідини з пам’яттю".
Рисунок 2.8 – Схема розподілення швидкостей і напружень при ламінарній течії ВПР у кільцевому каналі
Це ядро розділяє потік на два градієнтних шари. У першому шарі (I) похідна При знаходженні профілю швидкостей Рівняння руху:
Рівняння збереження маси:
Рівняння стану:
Реологічне рівняння стану:
де Реологічне рівняння для першого шару:
Реологічне рівняння для другого шару:
Умова рівноваги сил, які діють на ядро записується таким чином:
Граничні умови при відсутності ковзання:
Оскільки ядро рухається з постійною швидкістю
Крім того, повинна виконуватися умова:
Рівняння (2.63) з врахуванням (2.64) буде мати вигляд
Рівняння (2.64) показує, що при осесиметричному усталеному русі швидкість
Інтегруючи перше співвідношення (2.74) з врахуванням (2.75)
одержимо:
де Підставляючи реологічні рівняння (2.67) і (2.68) у друге співвідношення (2.74) та інтегруючи для кожного градієнтного шару одержимо: для першого шару (
для другого шару (
Невідомі постійні

Невідомі із системи (2.79) в явному вигляді не знаходять із-за їх наявності в рівняннях як під знаком логарифма, так і у вигляді одночленів, тобто внаслідок трансцендентності системи. Тому вважаючи постійні
Де величина А згідно з рівняннями (2.74) і (2.76) дорівнює
Систему рівнянь (2.79) і (2.80) можна звести до двох рівнянь. Інтегрування і виключення невідомих
де "
Ці два рівняння (2.82) і (2.83) перетворюються у вигляд:
де
де
За рівнянням (2.84) з урахуванням залежності (2.85) можна побудувати графік: На рисунку 2.7 приведена лише одна усереднена крива 2 для діапазону d, який найчастіше трапляється у практиці. Таким чином, за допомогою рівняння (2.87) можна знайти перепад тиску в кільцевому просторі за формулою:
Попередньо за кривою 2 рисунок 2.7 знаходять коефіцієнт " Графічний метод розрахунку втрат тиску при ламінарному русі в`язкопластичних рідин у трубах і кільцевому просторі розроблений К.Х. Гродде. Цей метод зручний і його точність визначається похибкою знаходження величини Гідравлічні втрати тиску в концентричному кільцевому просторі при ламінарному русі в’язкопластичної рідини наближено можна знайти за формулою, яка базується на принципі адитивності в’язкої і пластичної компонент тиску Для в’язкопластичної рідини можна застосовувати таку формулу для визначення втрат тиску в кільцевому просторі при ламінарному режимі руху:
де
Таблиця 2.3 – Коефіцієнти гідравлічних опорів в наземній обв’язці циркуляційної системи
де F - площа поперечного перерізу каналу труб або незвуженої частини кільцевого простору; Fмо - найменша площа поперечного перерізу прохідного каналу в замку або кільцевого простору за бурильним замком. Для визначення втрат тиску в бурильних замках всередині бурильної колони коефіцієнт місцевого опору визначають за формулою:
де
Для визначення втрат тиску в кільцевому просторі за бурильними замками коефіцієнт місцевого опору визначають за формулою:
де
де
Втрати тиску в прохідних каналах долота визначають за формулою:
де
Значення коефіцієнта витрати для різних форм прохідних отворів долота наведені в таблиці 2.4.
Таблиця 2.4 – Коефіцієнт витрати для різних форм насадок
Втрати тиску в турбобурі визначають за формулою:
де
де
Таблиця 2.5 – Значення коефіцієнта резерву і диференціального тиску
б) запобігання гідророзриву найслабших пластів. Тобто тиск промивальної рідини в затрубному просторі проти кожного пласта повинен бути менший від тиску, необхідного для гідророзриву даного пласта:
де
Оскільки значення 4 Вибирають турбобур. При турбінному способі буріння вибрана витрата промивальної рідини крім очищення вибою та виносу шламу, повинна забезпечувати роботу турбобура із заданою величиною крутного моменту. Тому необхідно підібрати такий турбобур, який задовольняє такі умови: а) діаметр корпуса повинен бути менший за діаметр долота більше, ніж на 10 мм; б) витрата промивальної рідини при номінальному режимі роботи близька до запроектованої; в) крутний момент турбобура не менше, ніж на 20 % більший за момент, необхідний для руйнування породи. Крутний момент турбобура при роботи на рідині заданої густини
де
5 Розраховують втрати тиску в елементах циркуляційної системи
де
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

 .
. .
. - це кількість рідини, яка протікає через даний переріз за одиницю часу.
- це кількість рідини, яка протікає через даний переріз за одиницю часу.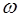 - це поперечний переріз, проведений перпендикулярно до напрямку руху рідини.
- це поперечний переріз, проведений перпендикулярно до напрямку руху рідини.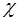 – це частина периметра живого перерізу потоку, по якому рідина дотикається (контактує) зі стінками, які обмежують потік.
– це частина периметра живого перерізу потоку, по якому рідина дотикається (контактує) зі стінками, які обмежують потік.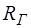 - це відношення площі живого перерізу потоку до змоченого периметра:
- це відношення площі живого перерізу потоку до змоченого периметра: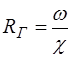 . (2.1)
. (2.1)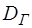 - це відношення почетвереної площі живого перерізу потоку до змоченого периметра:
- це відношення почетвереної площі живого перерізу потоку до змоченого периметра: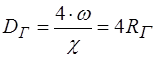 . (2.2)
. (2.2) - визначають як частку від ділення витрати на площу живого перерізу потоку:
- визначають як частку від ділення витрати на площу живого перерізу потоку: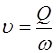 . (2.3)
. (2.3)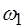 і
і 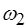 такого потоку справедливим є таке співвідношення, яке називається умовою нерозривності потоку.
такого потоку справедливим є таке співвідношення, яке називається умовою нерозривності потоку.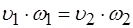 ,
, 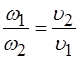 . (2.4)
. (2.4)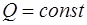 ,
,
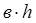
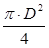
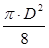
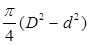
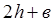
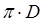
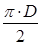
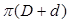
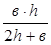
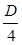
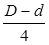
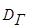
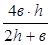
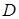
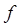
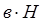
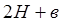
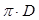
 (2.23)
(2.23) - реологічна константа, яка називається межею пластичності (текучості).
- реологічна константа, яка називається межею пластичності (текучості). а – тверде тіло Гука; б – ньютонівська рідина;
а – тверде тіло Гука; б – ньютонівська рідина; . (2.24)
. (2.24)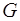 і
і  . Вона являє собою комбінацію моделей Гука і Ньютона, а ілюструється паралельним з’єднання пружини і амортизатора (рисунок 2.4,а).
. Вона являє собою комбінацію моделей Гука і Ньютона, а ілюструється паралельним з’єднання пружини і амортизатора (рисунок 2.4,а). . (2.25)
. (2.25) і в’язку
і в’язку  .
. (2.26)
(2.26)
 ), найчастіше використовують модель Оствальда–де Ваале з двома реологічними параметрами:
), найчастіше використовують модель Оствальда–де Ваале з двома реологічними параметрами: , (2.27)
, (2.27) і
і  - експериментальні константи;
- експериментальні константи; рівняння набуває форми закону Ньютона, при цьому
рівняння набуває форми закону Ньютона, при цьому  . Відхилення показника степеня
. Відхилення показника степеня  рідина є псевдопластична, а при
рідина є псевдопластична, а при  - дилатантна, (від латинського " dilatatio" – розширення, розтяг).
- дилатантна, (від латинського " dilatatio" – розширення, розтяг). , (2.28)
, (2.28)







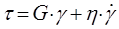

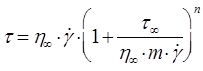


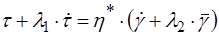

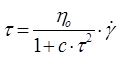

 - в’язкість при нескінченій швидкості зсуву, яка характеризує нахил лінійного відрізка кривої руху до осі абсцис при дуже високих швидкостях зсуву;
- в’язкість при нескінченій швидкості зсуву, яка характеризує нахил лінійного відрізка кривої руху до осі абсцис при дуже високих швидкостях зсуву;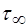 - константа, яка визначається ординатою точки перетину вказаного лінійного відрізка з віссю напружень;
- константа, яка визначається ординатою точки перетину вказаного лінійного відрізка з віссю напружень; - безрозмірна константа;
- безрозмірна константа; - уявна в’язкість при швидкостях зсуву, наближених до нуля;
- уявна в’язкість при швидкостях зсуву, наближених до нуля; , (2.29)
, (2.29) - час релаксації.
- час релаксації. , а у другому шарі (II)
, а у другому шарі (II)  .
. необхідно розв’язувати систему рівнянь (2.63) – (2.66) для кожного шару окремо, оскільки реологічне рівняння для кожного шару своє.
необхідно розв’язувати систему рівнянь (2.63) – (2.66) для кожного шару окремо, оскільки реологічне рівняння для кожного шару своє. . (2.63)
. (2.63) . (2.64)
. (2.64) . (2.65)
. (2.65) . (2.66)
. (2.66)
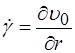 .
.
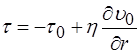 . (2.67)
. (2.67)
 . (2.68)
. (2.68) ,
,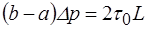 . (2.69)
. (2.69) . (2.70)
. (2.70) при
при  . (2.71)
. (2.71) при
при  . (2.72)
. (2.72)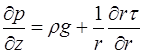 . (2.73)
. (2.73) і таким чином з (2.73) виходить, що
і таким чином з (2.73) виходить, що  є функція радіуса
є функція радіуса  , оскільки тиск є функцією
, оскільки тиск є функцією  , тобто знайдемо значення
, тобто знайдемо значення  , обумовлене силами тертя. Таким чином
, обумовлене силами тертя. Таким чином і
і  . (2.74)
. (2.74) , (2.75)
, (2.75) , (2.76)
, (2.76) ,
,  .
. . (2.77)
. (2.77)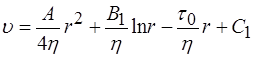 . (2.78)
. (2.78) , а також розміри ядра
, а також розміри ядра  і швидкість
і швидкість  (2.80)
(2.80) . (2.81)
. (2.81) із рівнянь (2.80) і (2.79) дає формулу:
із рівнянь (2.80) і (2.79) дає формулу: (2.82)
(2.82) " знаходять із рівняння Воларовича–Гуткіна:
" знаходять із рівняння Воларовича–Гуткіна: (2.83)
(2.83) (2.84)
(2.84) . (2.85)
. (2.85)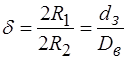 - відношення зовнішнього діаметра внутрішньої труби
- відношення зовнішнього діаметра внутрішньої труби 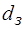 до внутрішнього діаметра зовнішньої труби
до внутрішнього діаметра зовнішньої труби  ;
; відношення подвоєної віддалі, яку відраховують від осі труби до зовнішньої межі ядра кільцевого потоку, до внутрішнього діаметра зовнішньої труби, причому:
відношення подвоєної віддалі, яку відраховують від осі труби до зовнішньої межі ядра кільцевого потоку, до внутрішнього діаметра зовнішньої труби, причому: ;
; - параметр Сен – Венана,
- параметр Сен – Венана,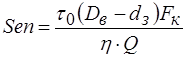 , (2.86)
, (2.86) - площа кільцевого перерізу
- площа кільцевого перерізу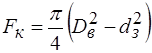 ,
, . (2.87)
. (2.87) .
. . (2.88)
. (2.88)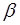 ". Для цього визначають параметр Сен–Венана за відомою витратою
". Для цього визначають параметр Сен–Венана за відомою витратою  та
та  .
. , (2.89)
, (2.89) - внутрішній діаметр кільця;
- внутрішній діаметр кільця; - зовнішній діаметр кільця.
- зовнішній діаметр кільця. ,
м4
,
м4
 , (2.103)
, (2.103)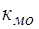 - дослідний коефіцієнт, який враховує особливості конфігурації місцевого опору. Для бурильних замків
- дослідний коефіцієнт, який враховує особливості конфігурації місцевого опору. Для бурильних замків 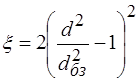 , (2.104)
, (2.104)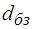 - найменший внутрішній діаметр бурильного замка.
- найменший внутрішній діаметр бурильного замка.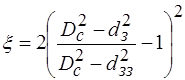 , (2.105)
, (2.105) - діаметр свердловини;
- діаметр свердловини;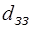 - зовнішній діаметр бурильного замка.
- зовнішній діаметр бурильного замка.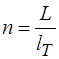 , (2.106)
, (2.106) - довжина колони бурильних одного типорозміру;
- довжина колони бурильних одного типорозміру;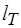 - довжина бурильної труби.
- довжина бурильної труби.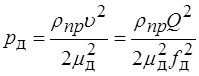 , (2.107)
, (2.107) - сумарна площа прохідних каналів (отворів) долота;
- сумарна площа прохідних каналів (отворів) долота;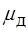 - коефіцієнт витрати, який залежить від форми отвору, фізичних властивостей рідини і тиску, при якому витікає рідина.
- коефіцієнт витрати, який залежить від форми отвору, фізичних властивостей рідини і тиску, при якому витікає рідина. , (2.108)
, (2.108) - постійна турбобура по перепаду тиску;
- постійна турбобура по перепаду тиску;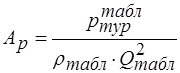 , (2.109)
, (2.109)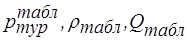 - відповідно перепад тиску в турбобурі при номінальному режимі його роботи на рідині з відомою густиною та витратою (за паспортними (табличними) даними конкретного турбобура).
- відповідно перепад тиску в турбобурі при номінальному режимі його роботи на рідині з відомою густиною та витратою (за паспортними (табличними) даними конкретного турбобура). , МПа
, МПа
 ,
, - тиск гідророзриву(поглинання) пласта, Па;
- тиск гідророзриву(поглинання) пласта, Па; - втрати тиску при русі промивальної рідини в затрубному просторі на шляху від розглядуваного об’єкта до устя свердловини.
- втрати тиску при русі промивальної рідини в затрубному просторі на шляху від розглядуваного об’єкта до устя свердловини. - вміст рідини в шламорідинному потоці без врахування відносних швидкостей;
- вміст рідини в шламорідинному потоці без врахування відносних швидкостей; ,
, - густина шламу, кг/м3;
- густина шламу, кг/м3; - глибина залягання підошви розглядуваного пласта, м;
- глибина залягання підошви розглядуваного пласта, м; - механічна швидкість буріння, м/с.
- механічна швидкість буріння, м/с. і витрати
і витрати  ,
, ,
,  - паспортні (довідкові) момент, густина та витрата турбобура.
- паспортні (довідкові) момент, густина та витрата турбобура. , (2.110)
, (2.110) - сумарні гідравлічні втрати тиску в елементах циркуляційної системи, Па;
- сумарні гідравлічні втрати тиску в елементах циркуляційної системи, Па; - втрати тиску в бурильних трубах, Па;
- втрати тиску в бурильних трубах, Па; - втрати тиску в кільцевому просторі за бурильними трубами, Па;
- втрати тиску в кільцевому просторі за бурильними трубами, Па; - втрати тиску в бурильних замках, Па;
- втрати тиску в бурильних замках, Па; - втрати тиску в обважнених бурильних трубах, Па;
- втрати тиску в обважнених бурильних трубах, Па; - втрати тиску в кільцевому просторі за обважненими бурильними трубами, Па;
- втрати тиску в кільцевому просторі за обважненими бурильними трубами, Па; - втрати тиску в наземній обв’язці (стояк, буровий шланг, ведуча труба, вертлюг), Па;
- втрати тиску в наземній обв’язці (стояк, буровий шланг, ведуча труба, вертлюг), Па; - втрати тиску в турбобурі,Па;
- втрати тиску в турбобурі,Па;



