
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
С помощью векторов инверсий.Содержание книги
Поиск на нашем сайте
Пара (αi, αj) называется инверсией перестановки α = (α1, α2,..., αn), если i < j и αi > αj. Инверсию (αi, αj) будем также называть j-инверсией перестановки α, тем самым явно указывая номер меньшего элемента в инверсии (αi, αj). Вектором инверсий перестановки α ∈ Sn называется последовательность целых чисел (d1, d2,..., dn) такая, что dj есть число j-инверсий перестановки α. Другими словами, dj есть число элементов перестановки α, больших αj и находящихся левее αj в последовательности (α1,..., αn), dj =| {αi | i < j & αi > αj} | 12. Например, для перестановки (4, 3, 5, 2, 1, 7, 8, 6, 9) вектором инверсий будет вектор (0, 1, 0, 3, 4, 0, 0, 2, 0). Вектор инверсий содержит информацию о структуре "беспорядка" перестановки. Такая информация оказывается полезной при разработке различных алгоритмов обработки данных. Процесс восстановления перестановки α = (α 1 ,..., α 5), имеющей вектор инверсий d = (0, 0, 2, 1, 1), выглядит так: i = 5, I5 = {1, 2, 3, 4, 5}, d5 + 1 = 2, α5 = 4; i = 4, I4 = {1, 2, 3, 5}, d4 + 1 = 2, α4 = 3; i = 3, I3 = {1, 2, 5}, d3 + 1 = 3, α3 = 1; i = 2, I2 = {2, 5}, d2 + 1 = 1, α2 = 5; i = 1, I1 = {2}, d1 + 1 = 1, α1 = 2; α = (2, 5, 1, 3, 4). Формализуем данный алгоритм в виде псевдокода. Очевидным образом можно сэкономить используемую память и уменьшить число операций, отказавшись от создания множества Ii и упорядочивания его элементов на каждом шаге i. Вместо этого достаточно хранить только лишь метки для уже вычеркнутых чисел из множества { 1, 2 ,..., n} и добавлять на шаге i метку для числа αi. Будем использовать массив ϕ размерности n с булевыми значениями его элементов true и false для создания таких меток. Алгоритм PConstrV (d1 ,..., dn) восстановления перестановки: α = (α1,..., αn) по ее вектору инверсий d = (d1,..., dn)
for k = 1 to n do ϕk:= true; for i = n downto 1 do begin j:= 1; m:= n; while j ≤ di or ϕm = false do begin if ϕj = true then j:= j + 1; m:= m − 1 end; αi:= m; ϕm:= false end.
Алгоритм PV Inv(n) генерации всех перестановок через векторы инверсий: for i = 0 to n! − 1 do begin % нахождение n-факториального FDecomp(n, i); % представления (d1,..., dn) числа i; PConstrV (d1,..., dn); % восстановление перестановки α по write(α1,..., αn) % вектору инверсий (d1,..., dn) end.
С помощью вложенных циклов. Будем говорить, что перестановка Алгоритм порождения подстановок с помощью вложенных циклов основан на следующей теореме.
Любую подстановку В качестве начальной перестановки берем
Цикл (
Конец цикла
Пока ( Печать
Сдвиг первых k элементов на одну позицию Пока (
Сдвиг первых k элементов на одну позицию Конец цикла Конец цикла Конец В порядке минимального изменения. Алгоритм строит последовательность, в которой разница между двумя последовательными перестановками еще меньше: каждая следующая образуется из предыдущей с помощью однократной транспозиции соседних элементов. Предположим, что уже построена последовательность перестановок элементов
В общем виде элемент 1 помещается между первой и последней позициями попеременно вперед и назад
procedure Perm(m:integer); {Основная процедура генерирования и вывода очередной перестановки} var k,k1,i:integer; begin if m=1 then {Нерекурсивная ветвь} begin for i:=1 to n do Write(P[i]:4); Writeln; end else {Рекурсивная ветвь} for i:=1 to m do begin Perm(m-1); if i<m then begin k1:=b(m,i); k:=P[k1]; P[k1]:=P[m]; P[m]:=k; end; end; end;
|
||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 949; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.46.108 (0.009 с.) |

 является циклом длины k степени d, если ее элементы
является циклом длины k степени d, если ее элементы  , получены из 1, 2, …, k циклическим сдвигом вправо на d позиций, остальные n – k элементов стационарны. Например, подстановка
, получены из 1, 2, …, k циклическим сдвигом вправо на d позиций, остальные n – k элементов стационарны. Например, подстановка  является циклом длины 4 степени 1.
является циклом длины 4 степени 1. на множестве
на множестве  можно представить в виде композиции
можно представить в виде композиции  , где
, где  — циклическая подстановка порядка i.
— циклическая подстановка порядка i.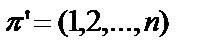 и сдвигаем на одну позицию вправо все элементы до тех пор, пока вновь не получим
и сдвигаем на одну позицию вправо все элементы до тех пор, пока вновь не получим  ; теперь сдвигаем циклически первые
; теперь сдвигаем циклически первые  элементов и снова повторяем сдвиг всех n элементов на одну позицию до тех пор, пока не получим уже имеющуюся перестановку; сдвигаем циклически ее первые
элементов и снова повторяем сдвиг всех n элементов на одну позицию до тех пор, пока не получим уже имеющуюся перестановку; сдвигаем циклически ее первые  элементов… и т.д., пока не переберем все
элементов… и т.д., пока не переберем все  перестановок. Ниже приведен алгоритм вложенных циклов.
перестановок. Ниже приведен алгоритм вложенных циклов. )
) ;
;
 )
)
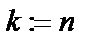
 и
и  )
)
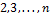 , обладающая этим свойством, например:
, обладающая этим свойством, например:  для
для  . Тогда требуемую последовательность перестановок элементов
. Тогда требуемую последовательность перестановок элементов 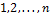 получим, вставляя элемент 1 всеми возможными способами в каждую перестановку элементов
получим, вставляя элемент 1 всеми возможными способами в каждую перестановку элементов 
 раз. На основе этой конструкции можнолегко получить рекурсивный алгоритм, генерирующий требуемую последовательность перестановок для произвольного
раз. На основе этой конструкции можнолегко получить рекурсивный алгоритм, генерирующий требуемую последовательность перестановок для произвольного  .
.


