
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обробка результатів прямих вимірювань.Содержание книги Поиск на нашем сайте
При прямих вимірюваннях визначають вибіркове середнє арифметичне значення
де Вибіркове середнє квадратичне відхилення
Випадкова похибка вимірювання
де Приладова похибка для вимірювальних величин
де Якщо розрахувати, що випадкова та приладова похибки незалежні, то загальна похибка
Обробка результатів непрямих вимірювань. При непрямих вимірюваннях результати прямих вимірювань підставляють у деяку функціональну залежність (робочу формулу)
де У (10) підставляють середні вибіркові значення результатів прямих вимірювань (
Абсолютну похибку
де Відносна похибка при непрямих вимірюваннях визначається як Механіка Лабораторна робота № 1.1 Вивчення кінематики і динаміки поступального руху на машині Атвуда
Мета роботи: визначити прискорення вільного падіння.
Теоретичні відомості (Теорія до даної роботи описана в лекційному курсі (інтерактивного комплексу Ч І), §1.2, §1.4.)
Миттєва швидкість характеризує зміну радіус-вектора в часі. Це швидкість в даний момент часу або в даній точці траєкторії. Вона дорівнює першій похідній радіуса-вектора по часу і напрямлена вздовж дотичної до траєкторії.
Вектор середньої швидкості рівний відношенню приросту радіуса-вектора Миттєве прискорення характеризує зміну швидкості в часі. Воно дорівнює першій похідній швидкості по часу або другій похідній радіуса-вектора по часу
Рівномірним поступольним називається рух зі сталою швидкістю Кінематика рівномірного руху: Рівноприскоренним називається рух зі сталим прискоренням (а=const). Кінематика рівноприскореного руху: Перший закон Ньютона: існують такі системи відліку в яких матеріальна точка (тіло) перебуває в стані спокою або рухається рівномірно і прямолінійно доти, поки дія з боку інших тіл не змусить її змінити цей стан. Другий закон Ньютона: швидкість зміни імпульсу матеріальної точка (тіла), рівна рівнодійній всіх діючих сил
Третій закон Ньютона: сили, з якими взаємодіють два тіла, рівні за модулем і протилежні за напрямком.
Неінерціальними називаються системи відліку, які рухаються з прискоренням відносно інерціальної системи.
Опис установки Та вивід робочої формули Машина Атвуда призначена для вивчення поступального руху тіл. Принцип дії приладу оснований на використанні законів Ньютона та рівнянь рівномірного та рівноприскореного рухів. Прилад зображений на рис. 1. Легкий блок вільно обертається навколо осі, що закріплена у верхній частині вертикальної стійки. Через блок перекинута нитка, на кінцях якої висять тягарці А і Б з рівними масами M. На ці тягарці зверху можна покласти ще один або декілька тягарців різних мас (m). Система тягарців при цьому виходить з рівноваги і починає рухатись прискорено. В момент проходження фотодатчика К 1 додатковий тягарець знімається, далі рух тягарця Б стає рівномірним. На шкалі секундоміра висвічується час рівномірного руху тягарця Б між фотодатчиками К 1, К 2. Розглянемо спочатку рух тягарця Б. Будемо користуватися нерухомою системою координат, центр якої суміщений з віссю блока. Вісь Ox направимо вниз. Нехай m - маса додаткового тягарця, що знаходиться на тягарі Б. На тягарець Б діють дві сили: сила тяжіння
де а – прискорення тягарця Б. Прискорення тягарця А рівне по величині прискоренню тягарця Б і направлене в протилежний бік (вважаємо, що нитка не розтягується).
Нехай сила натягу лівого кінця нитки буде
Якщо знехтувати силою тертя, то З рівнянь (1-3) отримаємо
З (4) видно, що рух в даному випадку рівноприскорений. Тягарці, рухаючись рівноприскорено, пройдуть шлях
де t 1 – час рівноприскореного руху. Тягарці, рухаючись рівномірно, пройдуть шлях
де u – швидкість рівномірного руху, t 2 - час рівномірного руху (вимірюється секундоміром).
Підставляючи a (4) і t 1 (6) в рівняння (5),отримаємо
З рівняння (8) визначимо прискорення вільного падіння
Хід роботи 1. Визначити шлях S 1 – рівноприскореного руху і S 2 – рівномірного руху тягарця Б за допомогою міліметрової шкали на стійці приладу. 2. Записати маси тягарців M і m. 3. Кнопку «Пуск» втиснути. 4. Додатковий тягарець покласти на тягарець Б, підняти у верхнє положення і кнопку «Пуск» відтиснути. 5. Натиснути послідовно кнопки “ Сброс ”, “ Пуск ” і зняти відлік часу t2 рівномірного руху тягарця Б. 6. Натиснути кнопки “ Сброс ”, дослід за пунктами 4-5 повторити 5 разів. 7. Визначити середнє значення t 2 . 8. Оцінити паспортні приладові похибки та похибки табличних величин. 9. За робочою формулою (9) обчислити прискорення вільного падіння. 10. Обчислити відносну і абсолютну похибки, записати кінцевий результат.
Результати вимірювань M = D M 0 = m = D m 0 = D S 0 = D t 0 =
Контрольні питання 1. Дати означення миттєвої швидкості. 2. Дати означення миттєвого прискорення. 3. Яку фізичну величину називають середньою швидкістю? 4. Які рухи називають рівномірним, рівноприскореним? Записати формули швидкості та шляху для цих рухів. 5. Які системи відліку називають інерціальними, неінерціальними? 6. Сформулювати закони Ньютона. 7. Намалювати і пояснити графіки залежностей 8. Вивести робочу формулу.
Лабораторна робота № 1.2
Визначення моменту інерції твердих тіл за допомогою крутильних коливань
Мета роботи: визначити момент інерції твердого тіла правильної форми.
Теоретичні відомості (Теорія до даної роботи описана в лекційному курсі (інтерактивного комплексу Ч І), §§1.9-1.10) При поступальному русі мірою інертних властивостей матеріальної точки (тіла) є маса, при обертальному русі її аналогом буде момент інерції, який рівний добутку маси матеріальної точки на квадрат відстані до центра або осі обертання
У випадку системи матеріальних точок (твердого тіла), що обертається навколо деякої осі OZ, момент інерції рівний сумі моментів інерції всіх матеріальних точок, з яких складається дана система
де Теорема Штейнера:момент інерції тіла І відносно довільної осі OZрівний моменту його інерції І 0 відносно паралельної осі, що проходить через центр мас тіла С, плюс добуток маси тіла m на квадрат віддалі d між осями Момент сили
його модуль рівний Момент імпульсу твердого тіла відносно точки О сновний закон динаміки обертального руху тіла відносно деякої нерухомої осі OZ: де Lz – момент імпульсу твердого тіла відносно осі, Mz – головний момент сил твердого тіла відносно осі
Момент імпульсу відносно деякої осі OZ можна записати як
Закону збереження моменту імпульсу твердого тіла відносно осі: якщо головний момент зовнішніх сил Mz відносно осі рівний нулю, то момент імпульсу твердого тіла відносно тієї ж осі зберігається,
|
|||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 154; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.176.63 (0.01 с.) |

 кількох вимірювань
кількох вимірювань , (5)
, (5) – значення і -го вимірювання,
– значення і -го вимірювання, 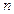 – число вимірювань.
– число вимірювань. величини
величини  . (6)
. (6) рівна
рівна
 , (7)
, (7) – коефіцієнт Стюдента. Він залежить від вибраної надійності Р та числа вимірів n. Надійність – це ймовірність попадання значення шуканої величини в заданий абсолютною похибкою довірчий інтервал. Для 5 вимірювань
– коефіцієнт Стюдента. Він залежить від вибраної надійності Р та числа вимірів n. Надійність – це ймовірність попадання значення шуканої величини в заданий абсолютною похибкою довірчий інтервал. Для 5 вимірювань 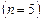 і при надійності
і при надійності  коефіцієнт Стьюдента рівний
коефіцієнт Стьюдента рівний  .
. (8)
(8) – приладова похибка,
– приладова похибка,  – паспортна похибка (див. таб.1).
– паспортна похибка (див. таб.1). при прямому вимірюванні визначається
при прямому вимірюванні визначається . (9)
. (9) , (10)
, (10) – значення окремих незалежних параметрів, отриманих при прямих вимірюваннях,а також значення постійних і табличних величин.
– значення окремих незалежних параметрів, отриманих при прямих вимірюваннях,а також значення постійних і табличних величин. )
) . (11)
. (11) визначають за формулою
визначають за формулою , (12)
, (12) – частинна похідна функції
– частинна похідна функції  по відповідному параметру
по відповідному параметру  – абсолютні похибки окремих величин
– абсолютні похибки окремих величин  (13)
(13) .
. рухомої точки до часу
рухомої точки до часу  , за який він відбувся
, за який він відбувся  .
. 
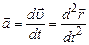 .
.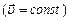 .
.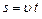 ;
;  ; а =0.
; а =0. ;
;  ; а=const.
; а=const. . Для сталої маси
. Для сталої маси  .
. .
. Інерціальними називаться системи відліку, відносно яких виконується перший закон Ньютона.
Інерціальними називаться системи відліку, відносно яких виконується перший закон Ньютона. і сила натягу правої частини нитки T 2. За другим законом Ньютона
і сила натягу правої частини нитки T 2. За другим законом Ньютона , (1)
, (1) , тоді
, тоді 
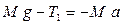 . (2)
. (2) . (3)
. (3)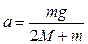 . (4)
. (4) , (5)
, (5)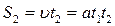 ,
, . (6)
. (6) . (8)
. (8) . (9)
. (9)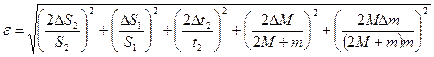
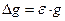 ..
.. ,
,  ,
,  , для рівномірного та рівноприскореного рухів.
, для рівномірного та рівноприскореного рухів.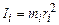 .
. ,
, – віддаль і -ої матеріальної точки від осі обертання OZ.
– віддаль і -ої матеріальної точки від осі обертання OZ. .
. відносно центра обертання О рівний векторному добутку радіуса-вектора
відносно центра обертання О рівний векторному добутку радіуса-вектора  , проведеного від центра обертання до точки прикладання сили, на силу
, проведеного від центра обертання до точки прикладання сили, на силу 
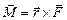 ,
,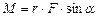 .
. .
. ,
, .
. , тобто Iz
, тобто Iz  = const.
= const.


