
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
До виконання лабораторних робітСодержание книги Поиск на нашем сайте
05-06-31 Методичні вказівки До виконання лабораторних робіт Із навчальної дисципліни фізика
Розділ «МЕХАНІКА»
для студентів інженерно-технічних напрямів підготовки денної, заочної та дистанційної форм навчання
Рекомендовано науково-методичною радою НВГП протокол № від..2013 р. РІВНЕ – 2013 Методичні вказівки до виконання лабораторних робіт із навчальної дисципліни фізика, розділ «МЕХАНІКА» для студентів інженерно-технічних напрямів підготовки денної, заочної та дистанційної форм навчання / О.Д. Кочергіна, В.Ф. Орленко, В.Р. Гаєвський, Рівне: НУВГП, 2013,- 35 с.
Упорядник: Кочергіна О.Д., асистент кафедри хімії та фізики; Орленко В.Ф., канд. фіз.-мат. наук, доцент кафедри хімії та фізики; Гаєвський В.Р., канд. фіз.-мат. наук, доцент кафедри хімії та фізики
Відповідальний за випуск Гаращенко В.І., доцент, кафедри хімії та фізики.
©Кочергіна О.Д.,Орленко В.Ф, Гаєвський В.Р, 2013 © НУВГП, 2013 ЗМІСТ Вступне заняття Вимірювання фізичних величин, похибки вимірювань- 4 Лабораторна робота № 1.1 Вивчення кінематики і динаміки поступального руху на машині Атвуда- 8 Лабораторна робота № 1.2 Визначення моменту інерції твердих тіл за допомогою крутильних коливань 12 Лабораторна робота № 1.3 Визначення моменту інерції маятника Максвела- 16 Лабораторна робота № 1.4 Вивчення центрального удару тіл- 20 Лабораторна робота № 1.5 Визначення моменту інерції маятника Обер бека- 24 Лабораторна робота №1.6 Визначення модуля Юнга за згином стержня- 28 Додаток 1 Приклад оформлення титульної сторінки- 33 Додаток 2 Приклад оформлення звіту- 34 Література- 32 Вступ Методичні вказівки до виконання лабораторних робіт з механіки створені з метою кращого засвоєння теоретичного та практичного курсу фізики, набуття студентами навичок експериментальних досліджень та обробки результатів вимірювань. В кожній роботі вказана мета і завдання, теоретичні відомості, опис експериментальної установки та хід роботи. Кафедрою розроблено оптитимальний режим виконання лабораторних робіт, кожна з яких має програмне забезпечення обробки результатів вимірювань. Це дає можливість студенту при необхідній підготовці виконати, оформити звіт і захистити лабораторну роботу на протязі одного заняття. Форма звіту приведена у додатках 1 та 2. Вступне заняття Вимірювання фізичних величин, похибки вимірювань
Види вимірювань Виміряти фізичну величину означає порівняти її з однорідною, яка прийнята за одиницю вимірювання. Основними одиницями виміру в СІ є метр (довжина), кілограм (маса), секунда (час), кельвін (температура), моль (кількість речовини), ампер (сила струму), кандела (сила світла). За способом одержання результату розрізняють прямі та непрямі вимірювання. § При прямих вимірюваннях шукана величина визначається безпосередньо за допомогою вимірювального приладу (розміри – лінійкою, штангенциркулем, мікрометром тощо; маса – терезами; час – секундоміром; сила струму – амперметром і т. д.). § Результат непрямого вимірювання визначається при підстановці значень прямих вимірювань до розрахункової формули.
Класифікація похибок Будь-яке вимірювання не може дати точного (істинного) значення величини. Це пов’язано з впливом різних факторів, по відношенню до яких з похибки вимірювань можна розділити: 1. промах – це результат використання несправного приладу, неправильної методики вимірювань, недбалих дій експериментатора, результат такого вимірювання відкидається; 2. систематична похибка повторюється від досліду до досліду або змінюється за певним законом. Джерелом систематичної похибки є неточність вимірювального приладу, недосконалість методики вимірювань; вона усувається шляхом введення поправок; 3. випадкова похибка змінюється від досліду до досліду і причина її виникнення зумовлена дією великої кількості непередбачуваних факторів. Така похибка може бути оцінена шляхом обробки результатів вимірювань із застосуванням теорії ймовірностей. Крім випадкової існує приладова похибка,яка визначається за паспортною похибкою приладу. § Для найпростіших приладів паспортна приладова похибка рівна половині ціни поділки вимірювального приладу. § Для цифрових приладів або приладів, покази яких змінюються стрибкоподібно паспортна похибка рівна ціні поділки. § Для постійних і табличних величин похибка рівна половині одиниці останнього розряду. Наприклад: g=9,8
Обробка результатів вимірювань ( метод Стюдента ) Будь-яке вимірювання має зміст, якщо відомо його абсолютну та відносну похибки. Абсолютна похибка визначає довірчий інтервал, у який з певною надійністю (ймовірністю) попадає шукана величина. В теорії похибок доводиться, що точне значення вимірюваної величини дорівнює середньому арифметичному з нескінченно великого числа результатів окремих вимірювань. Оскільки на практиці виконати цю умову неможливо, то користуються статистичними методами,одним з яких є метод Стюдента. Обрахунки можна розділити на два єтапи: 1. обробка результатів прямих вимірювань; 2. обробка результатів непрямих вимірювань.
Теоретичні відомості (Теорія до даної роботи описана в лекційному курсі (інтерактивного комплексу Ч І), §1.2, §1.4.)
Миттєва швидкість характеризує зміну радіус-вектора в часі. Це швидкість в даний момент часу або в даній точці траєкторії. Вона дорівнює першій похідній радіуса-вектора по часу і напрямлена вздовж дотичної до траєкторії.
Вектор середньої швидкості рівний відношенню приросту радіуса-вектора Миттєве прискорення характеризує зміну швидкості в часі. Воно дорівнює першій похідній швидкості по часу або другій похідній радіуса-вектора по часу
Рівномірним поступольним називається рух зі сталою швидкістю Кінематика рівномірного руху: Рівноприскоренним називається рух зі сталим прискоренням (а=const). Кінематика рівноприскореного руху: Перший закон Ньютона: існують такі системи відліку в яких матеріальна точка (тіло) перебуває в стані спокою або рухається рівномірно і прямолінійно доти, поки дія з боку інших тіл не змусить її змінити цей стан. Другий закон Ньютона: швидкість зміни імпульсу матеріальної точка (тіла), рівна рівнодійній всіх діючих сил
Третій закон Ньютона: сили, з якими взаємодіють два тіла, рівні за модулем і протилежні за напрямком.
Неінерціальними називаються системи відліку, які рухаються з прискоренням відносно інерціальної системи.
Опис установки Та вивід робочої формули Машина Атвуда призначена для вивчення поступального руху тіл. Принцип дії приладу оснований на використанні законів Ньютона та рівнянь рівномірного та рівноприскореного рухів. Прилад зображений на рис. 1. Легкий блок вільно обертається навколо осі, що закріплена у верхній частині вертикальної стійки. Через блок перекинута нитка, на кінцях якої висять тягарці А і Б з рівними масами M. На ці тягарці зверху можна покласти ще один або декілька тягарців різних мас (m). Система тягарців при цьому виходить з рівноваги і починає рухатись прискорено. В момент проходження фотодатчика К 1 додатковий тягарець знімається, далі рух тягарця Б стає рівномірним. На шкалі секундоміра висвічується час рівномірного руху тягарця Б між фотодатчиками К 1, К 2. Розглянемо спочатку рух тягарця Б. Будемо користуватися нерухомою системою координат, центр якої суміщений з віссю блока. Вісь Ox направимо вниз. Нехай m - маса додаткового тягарця, що знаходиться на тягарі Б. На тягарець Б діють дві сили: сила тяжіння
де а – прискорення тягарця Б. Прискорення тягарця А рівне по величині прискоренню тягарця Б і направлене в протилежний бік (вважаємо, що нитка не розтягується). Нехай сила натягу лівого кінця нитки буде
Якщо знехтувати силою тертя, то З рівнянь (1-3) отримаємо
З (4) видно, що рух в даному випадку рівноприскорений. Тягарці, рухаючись рівноприскорено, пройдуть шлях
де t 1 – час рівноприскореного руху. Тягарці, рухаючись рівномірно, пройдуть шлях
де u – швидкість рівномірного руху, t 2 - час рівномірного руху (вимірюється секундоміром).
Підставляючи a (4) і t 1 (6) в рівняння (5),отримаємо
З рівняння (8) визначимо прискорення вільного падіння
Хід роботи 1. Визначити шлях S 1 – рівноприскореного руху і S 2 – рівномірного руху тягарця Б за допомогою міліметрової шкали на стійці приладу. 2. Записати маси тягарців M і m. 3. Кнопку «Пуск» втиснути. 4. Додатковий тягарець покласти на тягарець Б, підняти у верхнє положення і кнопку «Пуск» відтиснути. 5. Натиснути послідовно кнопки “ Сброс ”, “ Пуск ” і зняти відлік часу t2 рівномірного руху тягарця Б. 6. Натиснути кнопки “ Сброс ”, дослід за пунктами 4-5 повторити 5 разів. 7. Визначити середнє значення t 2 . 8. Оцінити паспортні приладові похибки та похибки табличних величин. 9. За робочою формулою (9) обчислити прискорення вільного падіння. 10. Обчислити відносну і абсолютну похибки, записати кінцевий результат.
Результати вимірювань M = D M 0 = m = D m 0 = D S 0 = D t 0 =
Контрольні питання 1. Дати означення миттєвої швидкості. 2. Дати означення миттєвого прискорення. 3. Яку фізичну величину називають середньою швидкістю? 4. Які рухи називають рівномірним, рівноприскореним? Записати формули швидкості та шляху для цих рухів. 5. Які системи відліку називають інерціальними, неінерціальними? 6. Сформулювати закони Ньютона. 7. Намалювати і пояснити графіки залежностей 8. Вивести робочу формулу.
Лабораторна робота № 1.2
Визначення моменту інерції твердих тіл за допомогою крутильних коливань
Мета роботи: визначити момент інерції твердого тіла правильної форми.
Теоретичні відомості (Теорія до даної роботи описана в лекційному курсі (інтерактивного комплексу Ч І), §§1.9-1.10) При поступальному русі мірою інертних властивостей матеріальної точки (тіла) є маса, при обертальному русі її аналогом буде момент інерції, який рівний добутку маси матеріальної точки на квадрат відстані до центра або осі обертання
У випадку системи матеріальних точок (твердого тіла), що обертається навколо деякої осі OZ, момент інерції рівний сумі моментів інерції всіх матеріальних точок, з яких складається дана система
де Теорема Штейнера:момент інерції тіла І відносно довільної осі OZрівний моменту його інерції І 0 відносно паралельної осі, що проходить через центр мас тіла С, плюс добуток маси тіла m на квадрат віддалі d між осями Момент сили
його модуль рівний Момент імпульсу твердого тіла відносно точки О сновний закон динаміки обертального руху тіла відносно деякої нерухомої осі OZ: де Lz – момент імпульсу твердого тіла відносно осі, Mz – головний момент сил твердого тіла відносно осі Момент імпульсу відносно деякої осі OZ можна записати як
Закону збереження моменту імпульсу твердого тіла відносно осі: якщо головний момент зовнішніх сил Mz відносно осі рівний нулю, то момент імпульсу твердого тіла відносно тієї ж осі зберігається,
Хід роботи 1. Ввімкнути установку в мережу живлення і по черзі натиснути кнопки «Сеть», «Сброс». 2. Відхилити рамку таким чином, щоб її стрілка торкнулась осердя електромагніта, який утримує рамку в заданому положенні. 3. Натиснути кнопку «Пуск». Після 9 повних коливань натиснути кнопку «Стоп» і визначити період коливань рамки Т0 ( 4. Закріпити тіло з відомим моментом інерції І 1 (кулька). 5. Аналогічно повторити пункти 2, 3 визначити період коливань Т1. 6. Закріпити в рамці тіло, момент інерції якого потрібно визначити. 7. Аналогічно повторити пункти 2, 3 визначити період коливань Т. 8. Записати значення І 1. 9. Обчислити середні значення Т0, Т1, Т.. 10. Оцінити паспортні приладові похибки та похибки табличних величин. 11. За робочою формулою (4) обчислити І момент інерції досліджуваного тіла. 12. Обчислити відносну і абсолютну похибки, записати кінцевий результат.
Результати вимірювань I1= ∆(I1)0= ∆(T1)0=∆(T0)0=∆(T)0=
Контрольні запитання 1. Сформулювати і записати основний закон динаміки обертального руху твердого тіла відносно нерухомої осі. 2. Дати означення моменту імпульсу матеріальної точки і твердого тіла відносно центра і відносно осі. 3. Що таке момент сили? 4. Що називають моментом інерції матеріальної точки, твердого тіла? 5. Записати і пояснити теорему Штейнера. 6. Який зв’язок моменту імпульсу твердого тіла відносно осі з його моментом інерції. 7. Сформулювати закон збереження моменту імпульсу твердого тіла відносно осі.
Лабораторна робота № 1.3
Визначення моменту інерції маятника Максвела
Мета роботи: визначити момент інерції маятника Максвела.
Теоретичні відомості (Теорія до даної роботи описана в лекційному курсі (інтерактивного комплексу), §§1.9, 1.11-1.14, 1.17.)
Повна механічна енергія дорівнює сумі кінетичної і потенціальної Закон збереження повної механічної енергії: повна механічна енергія консервативної системи зберігається.
Консервативна система це система, в якій виконують роботу лише потенціальні сили, як внутрішні, так і зовнішні. Крім того, зовнішні сили повинні бути стаціонарні (незалежні від часу). Дисипативна (неконсервативна) система це система, в якій виконують роботу непотенціальні сили, наприклад сили тертя. Потенціальні сили це такі, робота яких не залежить від форми шляху. Наприклад,сила гравітації сила пружності. Непотенціальні сили це такі, робота яких залежить від форми шляху. Наприклад,сила тертя або опору. Момент інерції твердого тіла, що обертається навколо осі OZ, рівний сумі моментів інерції всіх матеріальних точок, з яких складається дана система де Кінетична енергія тіла при поступальному русі Кінетична енергія тіла при обертальному русі Хід роботи 1. В різних місцях намотування нитки визначити діаметр осі d (дослід повторити 5 разів). 2. Визначити відстань h між фотоелектричними датчиками за допомогою міліметрової шкали на вертикальній стійці приладу. 3. Намотати нитку підвісу таким чином, щоб диск маятника дотикався до полюса електромагніта, відтиснути кнопку “ Пуск ”. 4. Натиснути послідовно кнопки “ Сброс ”, “ Пуск ” і визначити час t руху маятника. 5. Дослід за пунктами 3,4 повторити 5 разів. 6. Оцінити паспортні приладові похибки та похибки табличних величин. 7. Обчислити середні значення dt. 8. За робочою формулою (7) обчислити І момент інерції маятника. 9. Обчислити відносну і абсолютну похибки, записати кінцевий результат
Результати вимірювань m = D m 0 = g = D g 0 = D d 0 = D h 0 = D t 0 =
Контрольні питання 1. Яку енергію називають кінетичною, потенціальною, повною механічною? 2. Сформулювати закон збереження механічної енергії. 3. Дати означення моменту інерції твердого тіла. 4. Записати вирази кінетичної енергії для поступального і обертального рухів. 5. Вивести вираз для кінетичної енергії обертального руху. 6. Які системи називають консервативними, дисипативними? 7. Які сили називають потенціальними, непотенціальними? Навести приклади. 8. Вивести робочу формулу. Лабораторна робота № 1.4 Вивчення центрального удару тіл
Мета роботи: в изначити силу взаємодії та коефіцієнт відновлення при центральному ударі.
Опис установки Загальний вигляд приладу показаний на рис. 1. На стійці 1 закріплений кронштейн 2, на якому за допомогою провідників підвішені кулі. Знизу стійка має шкалу 3 для визначення кутів відхилення куль. Кут відхилення можна фіксувати за допомогою електромагніта 4. Чає удару вимірюється мікросекундоміром 5.
Хід роботи 1. Записати початкові значення кутів 2. Ввімкнути прилад в мережу живлення. 3. Відтиснути кнопку «Пуск». 4. Праву кулю відвести в бік електромагніта 4 і зафіксувати її в цьому положенні, ліву кулю встановити нерухомо в положенні рівноваги. Записати кут відхилення правої кулі 5. Натиснути послідовно кнопки «Сброс», «Пуск». 6. Після удару куль визначити кути 7. Виконуючи послідовно пункти 3–6 повторити вимірювання не менше п’яти разів. 8. Оцінити паспортні похибки вимірювальних величин. 9. Обчислити середні значення кутів 10. За робочими формулами (7), (8) обчислити середню силу взаємодії куль F і коефіцієнт відновлення k. 11. Обчислити відносну і абсолютну похибки, записати кінцевий результат
Увага! Перед підстановкою
Результати вимірювань m1 = ∆(m1)0 = m2 = ∆(m2)0 = l = ∆(l)0 = g = ∆(g)0 = α 10= ∆(α)0 = α 20=
Контрольні запитання 1. Що таке удар двох тіл? 2. Сформулювати закон збереження імпульсу. 3. Сформулювати закон збереження механічної енергії. 4. Дати визначення центральних абсолютно пружнього і абсолютно непружнього ударів; записати закони збереження для цих двох випадків. 5. Що таке коефіцієнт відновлення? 6. Вивести робочу формулу для визначення середньої сили удару.
Лабораторна робота № 1.5 Визначення моменту інерції маятника Обер бека
Мета роботи: визначити момент інерції маятника Обербека.
Теоретичні відомості (Теорія до даної роботи описана в лекційному курсі (інтерактивного комплексу), §§1.9, 1.10) При поступальному русі мірою інертних властивостей матеріальної точки (тіла) є маса, при обертальному русі її аналогом буде момент інерції, який рівний добутку маси матеріальної точки на квадрат відстані до центра або осі обертання
У випадку системи матеріальних точок (твердого тіла), що обертається навколо деякої осі OZ, момент інерції рівний сумі моментів інерції всіх матеріальних точок, з яких складається дана система
де Теорема Штейнера:момент інерції тіла І відносно довільної осі OZрівний моменту його інерції І 0 відносно паралельної осі, що проходить через центр мас тіла С, плюс добуток маси тіла m на квадрат віддалі d між осями
Момент сили
його модуль рівний Момент імпульсу твердого тіла відносно точки
О сновний закон динаміки обертального руху тіла відносно деякої нерухомої осі OZ: Момент імпульсу відносно деякої осі OZ можна записати як
Закону збереження моменту імпульсу твердого тіла відносно осі: якщо головний момент зовнішніх сил Mz відносно осі рівний нулю, то момент імпульсу твердого тіла відносно тієї ж осі зберігається,
Опис установки Та вивід робочої формули Загальний вигляд маятника Обербека зображений на рис.1. На вертикальній стійці 1, закріплені два кронштейни: верхній рухомий 2 і нижній нерухомий 3. Власне маятник складається з двохступінчатого шківа 4, закріпленого на осі обертання; чотирьох взаємно перпендикулярних стержнів 5 і однакових тягарців 6, які можна переміщувати вздовж стержнів. Тягарці 6 розміщуються симетрично, щоб центр мас системи співпадав віссю обертання. Маятник приводиться в обертальний рух за допомогою тягарця 7, прикріпленого до нитки, намотаної на шків. Паралельно до нитки, на стійці розміщена масштабна лінійка. З її допомогою вимірюється висота падіння тягарця. На нижній втулці (за шківом) розміщений електромагніт, який після підключення до нього напруги живлення, утримує за допомогою муфти маятник в стані спокою. На верхньому і нижньому кронштейнах (2, 3) знаходяться фотоелектричні датчики. Вони виробляють електричні імпульси початку і кінця вимірювання часу мілісекундоміром. Момент інерції маятника може бути визначений з основного рівняння динаміки обертального руху
тобто вимірювання моменту інерції зводиться до визначення моменту сили М і кутового прискорення e. Визначимо силу, що діє на шків, яка рівна силі натягу нитки (силою тертя нехтуємо)
де m – маса тягарця (9), a – прискорення, з яким рухається тягарець. Тоді обертальний момент М дорівнює
де R – радіус шківа. Тягарець (9) опускається рівноприскорено, тому
де h – висота падіння тягарця, t – час падіння. Звідси лінійне прискорення
Кутове прискорення маятника обчислюється за формулою
Підставляючи (3), (5), (6) в (1) і врахувавши, що
Хід роботи 1. Виміряти діаметр шківа d. 2. Визначити віддаль між фотоелектричними датчиками h. 3. Визначити масу тягарця m. 4. Ввімкнути прилад в мережу живлення. 5. Натиснути послідовно кнопки «Сброс», «Пуск». 6. Намотати на шків 4 нитку таким чином, щоб тягарець 7 знаходився трохи вище фотоелектричного датчика 2, який розміщений на верхньому кронштейні і відтиснути кнопку «Пуск». 7. Натиснути кнопку «Пуск», привівши маятник в рух і зняти відлік часу t падіння тягарця. 8. Натиснути кнопки «Сброс» і дослід за пунктами 6-7 повторити 5 разів. 9. Оцінити паспортні приладові похибки та похибки табличних величин. 10. Обчислити середні значення t і d. 11. За робочою формулою (9) обчислити момент інерції маятника Обербека. 12. Обчислити відносну і абсолютну похибки, записати кінцевий результат
Результати вимірювань m = D m 0 = g = D g 0 = D d 0 = D h 0 = D t 0 =
Контрольні запитання 1. Вивести основний закон динаміки обертального руху твердого тіла відносно осі. 2. Що таке момент інерції твердого тіла? 3. Сформулювати теорему Штейнера. 4. Що називають моментом сили? Що називають плечем сили? 5. Дати значення моменту імпульсу відносно осі. Записати основне рівняння динаміки обертального руху через момент імпульсу. 6. Виразити момент імпульсу твердого тіла відносно осі через його момент інерції.
Лабораторна робота №1.6
Визначення модуля Юнга за згином стержня
Мета роботи: визначити модуль Юнга для сталі.
Хід роботи 1. Виміряти лінійкою довжину l стержня 2 від місця кріплення до індикатора. 2. Виміряти штангенциркулем ширину b і товщину h стержня не менше 5 разів у різних місцях стержня. 3. Шкалу індикатора 5 встановити в нульове положення. Навантажити шальку 3 вантажем 4. Визначити величину деформації l. Дослід повторити 5 разів, з однаковим навантаженням. 4. Оцінити паспортні приладові похибки та похибки табличних величин. 5. Обчислити середні значення величин b, h, l. 6. Обчислити за робочою формулою (2) значення модуля Юнга Е. 7. Обчислити відносну і абсолютну похибки, записати кінцевий результат
Результати вимірювань l = D l 0 = F = D F 0 = D b 0 = D h 0 = D l 0 =
Контрольні запитання 1. Що називають деформацією тіла? Які є види деформацій? 2. Яка природа сил пружності? 3. Що таке абсолютна деформація, відносна деформація? 4. Що таке механічна напруга? 5. Яку деформацію називають пружною, пластичною? 6. Нарисуйте і поясніть діаграму розтягу. 7. Сформулюйте закон Гука для деформацій розтягу і стиску. 8. Який фізичний зміст модуля Юнга?
Література
1. Навчальний посібник “Загальна фізика”, ч. І, під редакцією Ковалець М.О., Орленка В.Ф. Рівне, НУВГП, 2009 2. Трофимова Т.И. Курс физики.–М., "Высшая школа", 1990. 3. Детлаф А.А., Яворский В.М. Курс физики.–М., "Высшая школа", 1989. 4. Савельев И.В. Курс физики.–М., "Наука", 1989, т.1–3. 5. Зачек І.Р., Кравчук І.М., Романишин Б.М. та ін. Курс фізики. За ред. Лопатинського І.Є., Львів, “Бескид Біт” 2002. 6. Олексин Д.І., Мороз В.М. Загальна фізика. Частина 1. Конспект лекцій для студентів заочної форми навчання. Рівне, 2002, 073-89. 7. Дубчак Д.І., Ковалець М.О., Орленко В.Ф., Никонюк Є.С., Шляховий В.Л. Загальна фізика. Частина 2. Конспект лекцій для студентів заочної форми навчаня. Рівне, 2002, 073-90. 8. Кучерук І.М. та ін. Загальний курс фізики. У трьох томах, К., 1999. Додаток 1 Приклад оформлення титульної сторінки НУВГП Кафедра хімії та фізики Звіт З лабораторної роботи № Визначення моменту інерції твердого тіла. Виконав: Ст. МБ 11 Яковчук А.А | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

 , Δg0=0,05
, Δg0=0,05  .
. рухомої точки до часу
рухомої точки до часу  , за який він відбувся
, за який він відбувся  .
. 
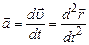 .
.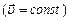 .
.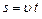 ;
;  ; а =0.
; а =0. ;
;  ; а=const.
; а=const. . Для сталої маси
. Для сталої маси  .
. .
. Інерціальними називаться системи відліку, відносно яких виконується перший закон Ньютона.
Інерціальними називаться системи відліку, відносно яких виконується перший закон Ньютона. і сила натягу правої частини нитки T 2. За другим законом Ньютона
і сила натягу правої частини нитки T 2. За другим законом Ньютона , (1)
, (1) , тоді
, тоді 
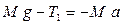 . (2)
. (2) . (3)
. (3)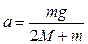 . (4)
. (4) , (5)
, (5)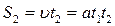 ,
, . (6)
. (6) . (8)
. (8) . (9)
. (9)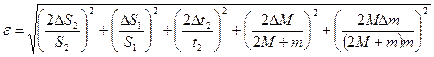
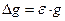 ..
.. ,
,  ,
,  , для рівномірного та рівноприскореного рухів.
, для рівномірного та рівноприскореного рухів.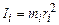 .
. ,
, – віддаль і -ої матеріальної точки від осі обертання OZ.
– віддаль і -ої матеріальної точки від осі обертання OZ. .
. відносно центра обертання О рівний векторному добутку радіуса-вектора
відносно центра обертання О рівний векторному добутку радіуса-вектора  , проведеного від центра обертання до точки прикладання сили, на силу
, проведеного від центра обертання до точки прикладання сили, на силу 
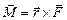 ,
,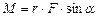 .
. .
. ,
, .
. , тобто Iz
, тобто Iz  = const.
= const. , де
, де  – час всіх коливань, n=10 – число повних коливань).
– час всіх коливань, n=10 – число повних коливань).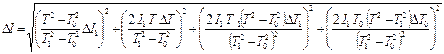

 ,
,
 ,
,
 ,
,
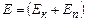 .
. .
. .
. .
.
 .
. ,
,  .
. .
.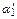 і
і  . При цьому також слід враховувати початкові значення кутів
. При цьому також слід враховувати початкові значення кутів  і
і 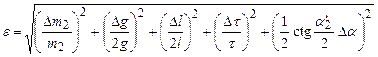 ,
, .
.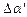 перевести у радіани!
перевести у радіани!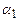 ,
,
 ,
,
 ,
,
 ,
,
 .
.
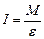 , (1)
, (1) , (2)
, (2) , (3)
, (3) , (4)
, (4) . (5)
. (5)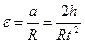 . (6)
. (6) (d – діаметр шківа), отримаємо формулу для знаходження моменту інерції маятника Обербека.
(d – діаметр шківа), отримаємо формулу для знаходження моменту інерції маятника Обербека. . (7)
. (7) ,
,



