
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Отчет по лабораторным работамСодержание книги Поиск на нашем сайте
По дисциплине: «Инженерные конструкции»
Выполнил: Студент ЗК-2-5 Васильева Б.О.
Проверил: Черемисинов А.Ю.
Воронеж Содержание
ЗАНЯТИЕ №1. НЕКОТОРЫЕ ПОНЯТИЯ В ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ. Сила Сила – величина, количественная мера механического взаимодействия материальных тел в механике.
Вектор силы обозначается латинскими буквами F, R, P, и др. с черточками над ними. Если черточки нет, значит у силы известна только её численная величина – модуль. Силаявляется величиной векторной. Силу изображают в виде направленного отрезка со стрелкой на конце, указывающего его направление. Прямая DE, вдоль которой направлена сила, называется линией действия силы. Её действие на тело определяется: 1) Численной величиной или модулем силы, 2) Направлением силы, 3) Точкой приложение силы (рис.1).
Например, будем прикладывать к стулу одну и туже по модулю силу F. · При приложении силы сверху вниз стул остается в состоянии покоя. · При положении силы снизу вверх – стул поднимается. · Приложим силу горизонтально к спинке стула – стул опрокинется.
Во всех случаях направление и место приложения силы различны – результат действия на стул разный, несмотря на то, что модуль силы F во всех случаях одинаков.
Правила: 1. Действие силы на тело не изменится, если её перенести по линии действия в любую точку тела (конечно – твердого тела). Поэтому вектор силы называют скользящим вектором. Если силу перенести в точку, не расположенную на этой линии, действие её на тело будет совсем другим. 2. Совокупность сил, действующих на какое-нибудь твердое тело, будем называть системой сил. 3. Тело, не скрепленное с другими телами, которому из данного положения можно сообщить любое перемещение в пространстве, называется свободным. 4. Если одну систему сил, действующий на свободное твердое тело, можно заменить другой системой, не изменяя при этом состояния покоя или движения, в котором находится тело, то такие две системы сил называются эквивалентными. Например, если системы сил, изображаемых на рис.2, а и рис.2, б, уравновешаны, то эти две системы сил будут эквиваленты друг другу. 5. Система сил, под действием которой свободное твердое тело может находиться в покое, называется уравновешенной или эквивалентный нулю. 6. Если в данной системы сил эквивалентна одной силе, то это сила называется равнодействующей данной системы сил. Таким образом, равнодействующая – это сила которая одна заменяет действие данной системы сил на твердое тело. Так как система сил F1 и F2 эквивалентна одной силе R (рис.2, б), то сила R называется равнодействующей данной системы сил. Силы F1 и F2 в свою очередь могут называться составляющими силы R.
Аксиомы статистики.
Аксиома 1. Если на свободное абсолютно твердое тело действуют две силы, то тело может находиться в равновесии тогда и только тогда, когда эти силы равны по модулю (F 1 = F 2) и направлены вдоль одной прямой в противоположные стороны (рис. 3). Аксиома 1 определяет простейшую уравновешенную систему сил, так как опыт показывает, что свободное тело, на которое действует только одна сила, находиться в равновесии не может.
Аксиома 2 (аксиома параллелограмма сил). Две силы, приложенные к телу в одной точке, имеют равнодействующую, приложенную в той же точке и изображаемую диагональю параллелограмма, построенного на этих силах, как на сторонах.
Величина равнодействующей:
Конечно,
Аксиома 3 (принцип противодействия). При всяком действие одного материального тела на другое имеет место такое же по величине, но противоположное по направлению противодействие. На рис.5 изображена балка, опирающаяся на стены концами A и B. Для выявления сил действия и противодействия отделим балку от стен. Тогда силы действия балки на стену выражаются силами Da и Db, приложенным к стенам, а силы противодействия – силами Ra и Rb, приложенными к балке, которые в дальнейшем будущем называть реакциями.
Момент Моментом силы называют вращательное усилие, создаваемое вектором силы относительно другого оюъекта(точки). Обязательное условие момента – точка, относительно которой создается момент не должна лежать на линии действия силы. Определяется как произведение силы F на плечо: M(F)=F*h h – плечо момента, определяется как кратчайшее расстояние от точки до линии действия силы. Пример момента силы: Размерность – [Н*м] (Ньютон на метр) либо кратные значения [кН*м] Например, если сила величиной 7 кН приложенная на расстоянии 35см от рассматриваемой точки дает момент М=7*0,35=2,45кНм. Примером момента силы – служит поворачивание гайки гаечным ключом. Гайки заворачиваются вращением, для этого к ним прикладывается момент, но сам момент возникает при воздействии нашей силы на гаечный ключ. Для того чтобы посильнее закрутить гайку надо взяться за ключ, как можно дальше от себя. Прикладывая ту же силу, получаем большую величину момента за счет увеличения его плеча(h2>h1). Плечом при этом служит расстояние от центра гайки до точки приложения силы. Плечо момента силы. Рассмотрим порядок определения плечо h момента, рис.7:
Знаки моментов: 1.Момент принимается положительным, если его вращение происходит против хода часовой стрелки. 2.Момент принимается отрицательным, если его вращение происходит по ходу часовой стрелки.
|
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 256; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.61.243 (0.007 с.) |


 Все теоремы и уравнения статистики выводится из нескольких исходных положений, принимаемых без математических доказательств называемых аксиомами или принципами статистики. Аксиомы статистики представляют собой результат обобщений многочисленных опытов и наблюдений над равновесием и движением тел, неоднократно подтвержденных практикой.
Все теоремы и уравнения статистики выводится из нескольких исходных положений, принимаемых без математических доказательств называемых аксиомами или принципами статистики. Аксиомы статистики представляют собой результат обобщений многочисленных опытов и наблюдений над равновесием и движением тел, неоднократно подтвержденных практикой. Вектор
Вектор  , равный диагонали параллелограмма, построенного на векторах
, равный диагонали параллелограмма, построенного на векторах  и
и  (рис.4), называется геометрической суммой векторов
(рис.4), называется геометрической суммой векторов  .
. .
. Такое равенство будет соблюдаться только при условии, что эти силы направлены по одной прямой в одну сторону. Если же векторы сил окажутся перпендикулярными, то
Такое равенство будет соблюдаться только при условии, что эти силы направлены по одной прямой в одну сторону. Если же векторы сил окажутся перпендикулярными, то 
 Следовательно, аксиому 3 можно еще формулировать так: две силы, приложенные к телу в одной точке, имеют равнодействующую, равную геометрической (векторной) сумме этих сил и приложенную в той же точке.
Следовательно, аксиому 3 можно еще формулировать так: две силы, приложенные к телу в одной точке, имеют равнодействующую, равную геометрической (векторной) сумме этих сил и приложенную в той же точке.
 Рис.7,а
Рис.7,а
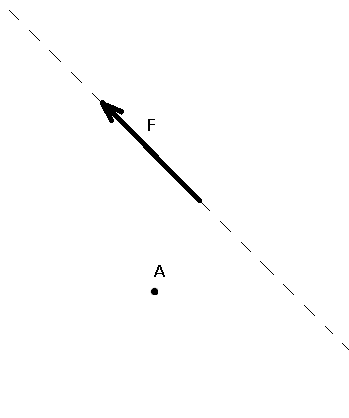 Рис.7,б
Рис.7,б
 Рис.7,в
Рис.7,в



