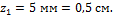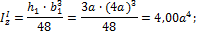Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Занятие №3. Построение эпюр.Содержание книги Поиск на нашем сайте
Рис.17 Эпюры сил и моментов, действующих поперечных сечениях балки при распределенной нагрузке
Необходимо учитывать правила: 1. Сумма сил действующих на систему равна нулю. 2. Сила направлена вверх (+). 3. Сила направлена вниз (-). 4. Если момент поворачивает по часовой стрелке (+), если против (-). Схема построения эпюр
80 * 1 – 100 + 30 * 2 * 3 – 4VB = 0 VB = 40кН
4VA – 80 * 3 – 100 + 30 * 2 * 1 = 0 VA = 100кН QA = Q2 = 100кН Q2-3 = 100 – 80 = 20кН Q = 100 – 80 – 60 = -40кН
M1-1 = 0 M2-2 = 100 * 1кН*М M4-4 = 100 * 2 – 80 * 1 = 120кН*М М5-5 = 120 – 100 = 20кН*М МB = 0
ЗАНЯТИЕ №4. ФОРМЫ СЕЧЕНИЯ, ПЛОЩАДИ СЕЧЕНИЯ, МОМЕНТЫ ИНЕРЦИИ И ОММЕНТЫ СОПРОТИВЛЕНИЯ ДЛЯ ОСНОВЫНХ ГЕОМЕТРИЧЕСКИХ ФОРМ КОНСТРУКЦИЙ. При растяжении и сжатии, прочность и жесткость стержней зависит от площади поперечных сечений стержней. При расчете на изгиб, кручение, а также сжатых стержней на устойчивость используют сплошные геометрические характеристики. -Статический момент -Момент инерции сечения -Момент сопротивления сечения Геометрические характеристики зависят так же от положения осей точек, относительно которых они вычисляются. Геометрические характеристики простой формы можно определить по специальным формулам. А также в таблицах ГОСТов – таблицы нормального сопротивления. Геометрические характеристики сложного сечения разбивают на ряд простых фигур и пользуются формулами, устанавливающими относительно различного сечения. Определим площадь сечения, момента инерции и момента сопротивления для квадрата и прямоугольника. a = 5см, b = 2см, h = 8см. F 1 = 5² = 25cм², Iz = Iy = 5⁴/12 = 52,1 F2 = 8*2 = 16см², Iz = 2*8³/12 = 85,3 F 1/ F2 = 1,5; I2/I1 = 1,6. Fy = 8*2³/12 = 1,3 Wz = 2*8²/6 = 21,3 Wy = 8*2²/6 = 5,3 Если мы берем прямоугольным ребром, то у него геометрические показатели будут лучше при меньшем мечении. b = 8 h = 2 F = 8*2 = 16cм² Iz = 8*2³/12 = 1,3 Wz = bh²/6 = 8*2²/6 = 5,3 Iy = 2*8³/12 = 85,3 Wy = hb²/6 = 2*8²/6 = 21,3
Сортамент – совокупность профилей и их размеров. Прокатные профили имеют стандарты, в которых указаны размеры сечения. Допуски на точность проекта.
ЗАНЯТИЕ №5. РАСЧЕТОВ ЦЕНТРОВ ТЯЖЕСТИ, МОМНТОВ И РАЗМЕРОВ ФИГУР. Пример 1. Найти положения центра тяжести фигуры, имеющей форму тавра (рис.18).
Решение. 1. Разбиваем изображенную на рис.18 фигуру на простые и присваиваем им номера 1 и 2. Центры тяжести каждой из простых фигур обозначаем соответственно с 1 и с 2. 2. Проводим через центры тяжести каждой из фигур оси z1, z2 и ось y. Ось y является осью симметрии фигуры, проходит через центры тяжести обеих простых фигур и всей фигуры также и поэтому индексации не имеет. 3. Выбираем в качестве начала координат центр тяжести второй фигуры c 2 и в качестве оси, относительно которой будем производить все вычисления, ось z 2. 4. Вычислим статический момент площади фигуры относительно оси z 2:
В формуле (а) координата центра тяжести второй простой фигуры 4. Находим координату центра тяжести всей фигуры, используя выражение (7):
Найденное значение координаты центра тяжести отложим вдоль оси y вверх от точки c 2, так как это значение положительное. Полученную точку обозначим буквой C. Ось z C, проведенная через центр тяжести всей фигуры будет одной из центральных осей фигуры. Вторая центральная ось фигуры в данном примере не определяется, так как этой осью является ось симметрии y. Статические моменты S y простых фигур и всей фигуры относительно этой оси равны нулю. В соответствии с выражением (7) координата центра тяжести всей фигуры z C = 0. Анализируя полученное решение, можно сделать вывод о том, что при определении центра тяжести для сложных фигур очень важно удачно выбрать начало координат и, соответственно, оси, относительно которых производятся все вычисления. Как уже отмечалось выше, начало координат следует помещать в центр тяжести одной из простых фигур.
Пример 2. Определить положение центра тяжести неравнобокого уголка 160
Решение. Пренебрегая загружением полок уголка, разбиваем фигуру на два прямоугольника, как показано на рис. 19. Для первого (1) прямоугольника
Для второго (2) прямоугольника
Координаты центра тяжести сечения определяем по формулам:
По данным сортамента с учетом закруглений координаты центра тяжести равны zc= 2,28см; yc= 5,23см. Для проверки правильности вычислений определим статические моменты относительно центральных осей, которые должны быть равны нулю:
Графическая проверка: точка С должна находиться на отрезке С 1 С 2.
Пример 3. Определить осевые моменты инерции фигуры, приведенной на рис.20, относительно центральных осей z c и y c.
Решение: В примере 3 для изображенной на рис.20 фигуры было определено положение центра тяжести С. Координата центра тяжести откладывалась от оси z 2 и составила y c =3,5 см. Вычислим расстояния a 1 и a 2 между осями z 1 и z c и осями z 2 и z c. Эти расстояния составили соответственно a 1 =3,5 см и a 2 = -3,5 см. Так как исходные оси z 1 и z 2 являются центральными осями для простых фигур в виде прямоугольников, для определения момента инерции фигуры относительно оси z c воспользуемся формулой.
Момент инерции относительно оси y c получим путем сложения моментов инерции простых фигур относительно этой же оси, так как ось y c является общей центральной осью для простых фигур и для всей фигуры.
Центробежный момент инерции относительно осей zc и y c равен нулю, так как ось инерции y c является главной осью (осью симметрии фигуры).
Пример 4. Определить момент инерции сечения, показанного на рис. 21, относительно оси симметрии, a =10 см.
Решение. Разбиваем заданное сечение на простейшие элементы: I - Равнобедренный треугольник, II - прямоугольник, III - круг. Момент инерции сложной фигуры относительно оси z согласно формуле:
Определяем моменты инерции слагаемых простейших элементов: Для равнобедренного треугольника:
для прямоугольника согласно формуле:
для круга согласно формуле:
Окончательно получим: I z= 4,0 a 4 + 10,67 a 4 - 0,0491 a 4 = 14,6 a 4 = 14,6×104 = 1,46×105 см4.
Пример 5. Определить момент инерции симметричного сечения, показанного на рис. 22, относительно вертикальной оси симметрии y. Двутавр №10 (ГОСТ 8239-56). Швеллер №5 (ГОСТ 8240-56).
Решение. Разбиваем исходное сечение на простейшие элементы, моменты инерций которых приводятся в справочниках: I - двутавр, II и III - швеллеры. По сортаменту на стандартные прокатные профили имеем: Для двутавра №10 (ГОСТ 8239-56): H =10 см, B =7 см, F =14,2 см2, I x=244 см4, I y=35,3 см4. Для швеллера №5 (ГОСТ 8240-56): h =5 см, b =3,7 см, F =6,90 см2, I x=26,1 см4, I y=8,41 см4, x 0=1,35 см. Момент инерции сечения относительно оси y согласно
т.к. оба швеллера расположены идентично относительно оси y. Для двутавра Для швеллера Окончательно имеем:
Пример 6. Чему равен размер b (в см)фигуры, изображенной на рис. 23, если момент инерции фигуры относительно оси z1 равен 1000 см4?
Решение. Выразим момент инерции относительно оси z через неизвестный размер сечения b, воспользовавшись формулами, учитывая, что расстояние между осями z и z 1 равно 7 см:
Решая выражение (а) относительно размера сечения b, получим:
Пример 7. Какая из фигур, изображенных на рис.24, имеет больший момент инерции относительно оси z, если обе фигуры имеют одинаковую площадь A =400 см2?
Решение. 1. Выразим площади фигур через их размеры и определим: а) диаметр сечения для круглого сечения:
Откуда
б) размер стороны квадрата: A = a 2. Откуда
2. Вычисляем момент инерции для круглого сечения:
3. Вычисляем момент инерции для сечения квадратной формы:
Сравнивая полученные результаты, приходим к выводу, что наибольшим моментом инерции будет обладать сечение квадратной формы по сравнению с сечение круглой формы при одинаковой у них площади.
|
||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 737; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.006 с.) |

 Эпюра - графическая схема решения задачи сопромата при расчете прочностных характеристик и действующих нагрузок на материал. Она отражает зависимость изгибающих моментов от длины нагруженного участка какого-либо элемента. Это может быть балка либо ферма, другая несущая конструкция. Эпюры строить в произвольном масштабе и подписывают размерности.
Эпюра - графическая схема решения задачи сопромата при расчете прочностных характеристик и действующих нагрузок на материал. Она отражает зависимость изгибающих моментов от длины нагруженного участка какого-либо элемента. Это может быть балка либо ферма, другая несущая конструкция. Эпюры строить в произвольном масштабе и подписывают размерности. Рис.16 Эпюры сил и моментов, действующих в поперечных сечениях балки
Рис.16 Эпюры сил и моментов, действующих в поперечных сечениях балки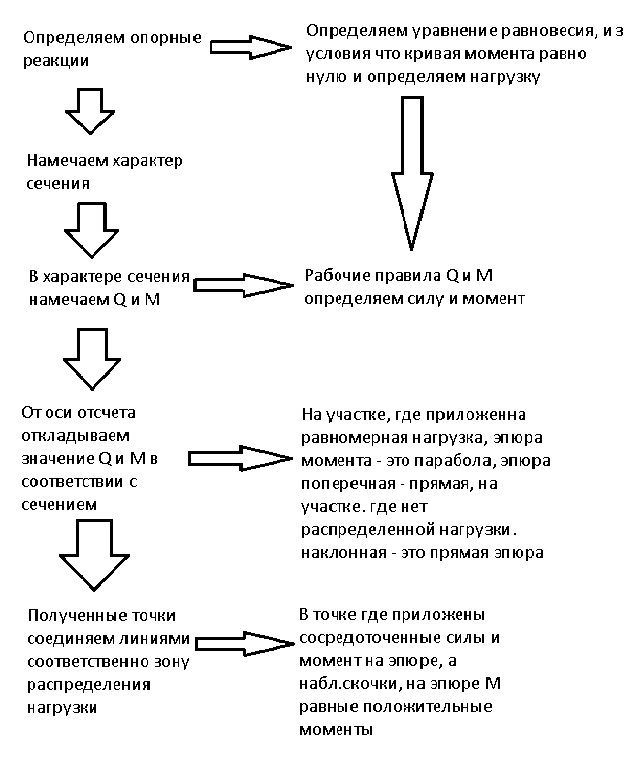






 , так как ось z 2, относительно которой определялся статический момент площади, проходит через центр тяжести второй фигуры. В соответствии с основным своим свойством статический момент площади относительно любой центральной оси равен нулю. В связи с этим для сокращения арифметических вычислений при определении положения центра тяжести сложных фигур рекомендуется выбирать в качестве начала координат центр тяжести одной из простых фигур.
, так как ось z 2, относительно которой определялся статический момент площади, проходит через центр тяжести второй фигуры. В соответствии с основным своим свойством статический момент площади относительно любой центральной оси равен нулю. В связи с этим для сокращения арифметических вычислений при определении положения центра тяжести сложных фигур рекомендуется выбирать в качестве начала координат центр тяжести одной из простых фигур.
 100
100