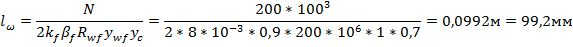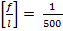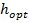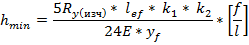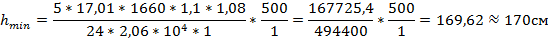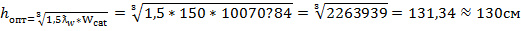Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кафедра мелиорации водоснабжения и геодезииСодержание книги
Поиск на нашем сайте
Министерство сельского хозяйства Российской Федерации ФГБОУ ВО «Воронежский государственный аграрный университет имени императора Петра I» Факультет землеустройства и кадастров Кафедра мелиорации водоснабжения и геодезии Отчет по лабораторным работам По дисциплине: «Инженерные конструкции»
Выполнил: Студент ЗК-2-5 Васильева Б.О.
Проверил: Черемисинов А.Ю.
Воронеж Содержание
ЗАНЯТИЕ №1. НЕКОТОРЫЕ ПОНЯТИЯ В ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ. Сила Сила – величина, количественная мера механического взаимодействия материальных тел в механике.
Вектор силы обозначается латинскими буквами F, R, P, и др. с черточками над ними. Если черточки нет, значит у силы известна только её численная величина – модуль. Силаявляется величиной векторной. Силу изображают в виде направленного отрезка со стрелкой на конце, указывающего его направление. Прямая DE, вдоль которой направлена сила, называется линией действия силы. Её действие на тело определяется: 1) Численной величиной или модулем силы, 2) Направлением силы, 3) Точкой приложение силы (рис.1).
Например, будем прикладывать к стулу одну и туже по модулю силу F. · При приложении силы сверху вниз стул остается в состоянии покоя. · При положении силы снизу вверх – стул поднимается. · Приложим силу горизонтально к спинке стула – стул опрокинется.
Во всех случаях направление и место приложения силы различны – результат действия на стул разный, несмотря на то, что модуль силы F во всех случаях одинаков.
Правила: 1. Действие силы на тело не изменится, если её перенести по линии действия в любую точку тела (конечно – твердого тела). Поэтому вектор силы называют скользящим вектором. Если силу перенести в точку, не расположенную на этой линии, действие её на тело будет совсем другим. 2. Совокупность сил, действующих на какое-нибудь твердое тело, будем называть системой сил. 3. Тело, не скрепленное с другими телами, которому из данного положения можно сообщить любое перемещение в пространстве, называется свободным. 4. Если одну систему сил, действующий на свободное твердое тело, можно заменить другой системой, не изменяя при этом состояния покоя или движения, в котором находится тело, то такие две системы сил называются эквивалентными. Например, если системы сил, изображаемых на рис.2, а и рис.2, б, уравновешаны, то эти две системы сил будут эквиваленты друг другу. 5. Система сил, под действием которой свободное твердое тело может находиться в покое, называется уравновешенной или эквивалентный нулю. 6. Если в данной системы сил эквивалентна одной силе, то это сила называется равнодействующей данной системы сил. Таким образом, равнодействующая – это сила которая одна заменяет действие данной системы сил на твердое тело. Так как система сил F1 и F2 эквивалентна одной силе R (рис.2, б), то сила R называется равнодействующей данной системы сил. Силы F1 и F2 в свою очередь могут называться составляющими силы R.
Аксиомы статистики.
Аксиома 1. Если на свободное абсолютно твердое тело действуют две силы, то тело может находиться в равновесии тогда и только тогда, когда эти силы равны по модулю (F 1 = F 2) и направлены вдоль одной прямой в противоположные стороны (рис. 3). Аксиома 1 определяет простейшую уравновешенную систему сил, так как опыт показывает, что свободное тело, на которое действует только одна сила, находиться в равновесии не может.
Аксиома 2 (аксиома параллелограмма сил). Две силы, приложенные к телу в одной точке, имеют равнодействующую, приложенную в той же точке и изображаемую диагональю параллелограмма, построенного на этих силах, как на сторонах.
Величина равнодействующей:
Конечно,
Аксиома 3 (принцип противодействия). При всяком действие одного материального тела на другое имеет место такое же по величине, но противоположное по направлению противодействие. На рис.5 изображена балка, опирающаяся на стены концами A и B. Для выявления сил действия и противодействия отделим балку от стен. Тогда силы действия балки на стену выражаются силами Da и Db, приложенным к стенам, а силы противодействия – силами Ra и Rb, приложенными к балке, которые в дальнейшем будущем называть реакциями.
Момент Моментом силы называют вращательное усилие, создаваемое вектором силы относительно другого оюъекта(точки). Обязательное условие момента – точка, относительно которой создается момент не должна лежать на линии действия силы. Определяется как произведение силы F на плечо: M(F)=F*h h – плечо момента, определяется как кратчайшее расстояние от точки до линии действия силы. Пример момента силы: Размерность – [Н*м] (Ньютон на метр) либо кратные значения [кН*м] Например, если сила величиной 7 кН приложенная на расстоянии 35см от рассматриваемой точки дает момент М=7*0,35=2,45кНм. Примером момента силы – служит поворачивание гайки гаечным ключом. Гайки заворачиваются вращением, для этого к ним прикладывается момент, но сам момент возникает при воздействии нашей силы на гаечный ключ. Для того чтобы посильнее закрутить гайку надо взяться за ключ, как можно дальше от себя. Прикладывая ту же силу, получаем большую величину момента за счет увеличения его плеча(h2>h1). Плечом при этом служит расстояние от центра гайки до точки приложения силы. Плечо момента силы. Рассмотрим порядок определения плечо h момента, рис.7:
Знаки моментов: 1.Момент принимается положительным, если его вращение происходит против хода часовой стрелки. 2.Момент принимается отрицательным, если его вращение происходит по ходу часовой стрелки.
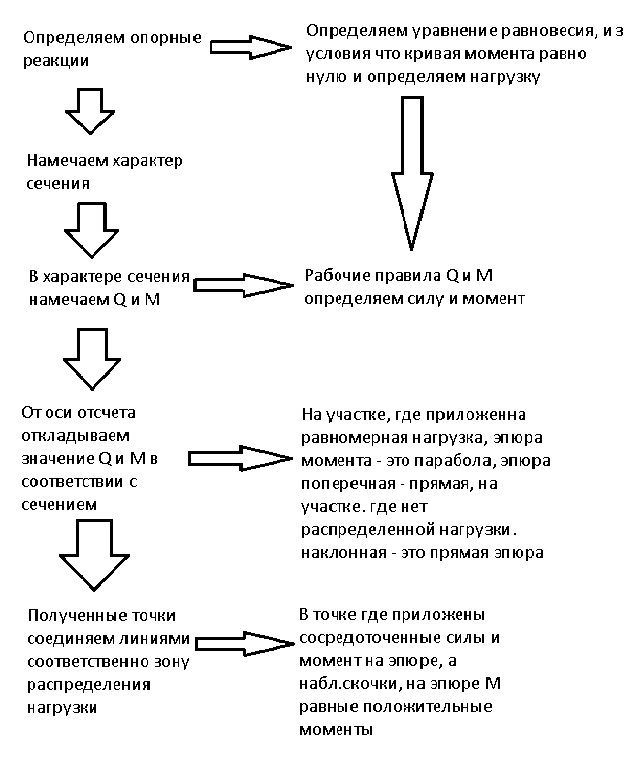
Схема построения эпюр
80 * 1 – 100 + 30 * 2 * 3 – 4VB = 0 VB = 40кН
4VA – 80 * 3 – 100 + 30 * 2 * 1 = 0 VA = 100кН QA = Q2 = 100кН Q2-3 = 100 – 80 = 20кН Q = 100 – 80 – 60 = -40кН
M1-1 = 0 M2-2 = 100 * 1кН*М M4-4 = 100 * 2 – 80 * 1 = 120кН*М М5-5 = 120 – 100 = 20кН*М МB = 0
Пример 1. Найти положения центра тяжести фигуры, имеющей форму тавра (рис.18).
Решение. 1. Разбиваем изображенную на рис.18 фигуру на простые и присваиваем им номера 1 и 2. Центры тяжести каждой из простых фигур обозначаем соответственно с 1 и с 2. 2. Проводим через центры тяжести каждой из фигур оси z1, z2 и ось y. Ось y является осью симметрии фигуры, проходит через центры тяжести обеих простых фигур и всей фигуры также и поэтому индексации не имеет. 3. Выбираем в качестве начала координат центр тяжести второй фигуры c 2 и в качестве оси, относительно которой будем производить все вычисления, ось z 2. 4. Вычислим статический момент площади фигуры относительно оси z 2:
В формуле (а) координата центра тяжести второй простой фигуры 4. Находим координату центра тяжести всей фигуры, используя выражение (7):
Найденное значение координаты центра тяжести отложим вдоль оси y вверх от точки c 2, так как это значение положительное. Полученную точку обозначим буквой C. Ось z C, проведенная через центр тяжести всей фигуры будет одной из центральных осей фигуры. Вторая центральная ось фигуры в данном примере не определяется, так как этой осью является ось симметрии y. Статические моменты S y простых фигур и всей фигуры относительно этой оси равны нулю. В соответствии с выражением (7) координата центра тяжести всей фигуры z C = 0. Анализируя полученное решение, можно сделать вывод о том, что при определении центра тяжести для сложных фигур очень важно удачно выбрать начало координат и, соответственно, оси, относительно которых производятся все вычисления. Как уже отмечалось выше, начало координат следует помещать в центр тяжести одной из простых фигур.
Пример 2. Определить положение центра тяжести неравнобокого уголка 160
Решение. Пренебрегая загружением полок уголка, разбиваем фигуру на два прямоугольника, как показано на рис. 19. Для первого (1) прямоугольника
Для второго (2) прямоугольника
Координаты центра тяжести сечения определяем по формулам:
По данным сортамента с учетом закруглений координаты центра тяжести равны zc= 2,28см; yc= 5,23см. Для проверки правильности вычислений определим статические моменты относительно центральных осей, которые должны быть равны нулю:
Графическая проверка: точка С должна находиться на отрезке С 1 С 2.
Пример 3. Определить осевые моменты инерции фигуры, приведенной на рис.20, относительно центральных осей z c и y c.
Решение: В примере 3 для изображенной на рис.20 фигуры было определено положение центра тяжести С. Координата центра тяжести откладывалась от оси z 2 и составила y c =3,5 см. Вычислим расстояния a 1 и a 2 между осями z 1 и z c и осями z 2 и z c. Эти расстояния составили соответственно a 1 =3,5 см и a 2 = -3,5 см. Так как исходные оси z 1 и z 2 являются центральными осями для простых фигур в виде прямоугольников, для определения момента инерции фигуры относительно оси z c воспользуемся формулой.
Момент инерции относительно оси y c получим путем сложения моментов инерции простых фигур относительно этой же оси, так как ось y c является общей центральной осью для простых фигур и для всей фигуры.
Центробежный момент инерции относительно осей zc и y c равен нулю, так как ось инерции y c является главной осью (осью симметрии фигуры).
Пример 4. Определить момент инерции сечения, показанного на рис. 21, относительно оси симметрии, a =10 см.
Решение. Разбиваем заданное сечение на простейшие элементы: I - Равнобедренный треугольник, II - прямоугольник, III - круг. Момент инерции сложной фигуры относительно оси z согласно формуле:
Определяем моменты инерции слагаемых простейших элементов: Для равнобедренного треугольника:
для прямоугольника согласно формуле:
для круга согласно формуле:
Окончательно получим: I z= 4,0 a 4 + 10,67 a 4 - 0,0491 a 4 = 14,6 a 4 = 14,6×104 = 1,46×105 см4.
Пример 5. Определить момент инерции симметричного сечения, показанного на рис. 22, относительно вертикальной оси симметрии y. Двутавр №10 (ГОСТ 8239-56). Швеллер №5 (ГОСТ 8240-56).
Решение. Разбиваем исходное сечение на простейшие элементы, моменты инерций которых приводятся в справочниках: I - двутавр, II и III - швеллеры. По сортаменту на стандартные прокатные профили имеем: Для двутавра №10 (ГОСТ 8239-56): H =10 см, B =7 см, F =14,2 см2, I x=244 см4, I y=35,3 см4. Для швеллера №5 (ГОСТ 8240-56): h =5 см, b =3,7 см, F =6,90 см2, I x=26,1 см4, I y=8,41 см4, x 0=1,35 см. Момент инерции сечения относительно оси y согласно
т.к. оба швеллера расположены идентично относительно оси y. Для двутавра Для швеллера Окончательно имеем:
Пример 6. Чему равен размер b (в см)фигуры, изображенной на рис. 23, если момент инерции фигуры относительно оси z1 равен 1000 см4?
Решение. Выразим момент инерции относительно оси z через неизвестный размер сечения b, воспользовавшись формулами, учитывая, что расстояние между осями z и z 1 равно 7 см:
Решая выражение (а) относительно размера сечения b, получим:
Пример 7. Какая из фигур, изображенных на рис.24, имеет больший момент инерции относительно оси z, если обе фигуры имеют одинаковую площадь A =400 см2?
Решение. 1. Выразим площади фигур через их размеры и определим: а) диаметр сечения для круглого сечения:
Откуда
б) размер стороны квадрата: A = a 2. Откуда
2. Вычисляем момент инерции для круглого сечения:
3. Вычисляем момент инерции для сечения квадратной формы:
Сравнивая полученные результаты, приходим к выводу, что наибольшим моментом инерции будет обладать сечение квадратной формы по сравнению с сечение круглой формы при одинаковой у них площади.
Пример 1.
Требуется определить необходимую длину фланговых швов при расчетном сопротивлении Rwf = 200 МПа, ywf = 1. Коэффициенты β f = 0,9 и yс = 0,7. Катет углового шва указан на расчетной схеме: kt=tл/2=16/2=8 мм – это катет углового шва. Из условия прочности на условный разрез по металлу шва определяем расчетную длину шва:
kf – катет углового шва (kf = 8мм) β f – коэффициент, зависящий от технологических, конструктивных и геометрических факторов (β f= 0,9) Rwf = расчетное сопротивление угловых швов срезу по металлу шва (Rwf = 200МПа) ywf = коэффициент условий работы шва, равный 1,0 y c = коэффициент условий работы конструкции (y c = 0,7)
Так расчетная длина шва принимается меньше его полной длинны на 10мм, то полная длина шва определяется как: ln = lω + 10 = 99,2 + 10 = 109,2 мм Принимаем длину шва: ln = 110мм = 11см
Электроды. Э38, Э42, Э46, Э50 –для сварки низколегированных и низкоуглеродистых сталей с временным сопротивлением до 500 МПа Вариант Рассчитать сварной двухригельный плоский затвор -ширина отверстия в свету l = 16м -глубина воды над порогом в B5 с учетом ветрового нагона волны H=4,4м -материал затвора – сталь марки C245 -сварка получена электродами типа Э42А Назначение высоты ригеля. Расчет высоты сечения ригель производится на основе выполнения 2-ух условий: А) Допустимая относительность прогиба Б) Обеспечение минимальной металлоемкости балки Определяем минимальную высоту сечения ригеля. h1 ≈ (0,5:0,6)h = (100:120)см h1 = hef2 + tf2 + tf2ˈ + t0 = 100 + 2 + 2 + 1 = 105см
Определим оптимальную высоту
Принимаем h=hmin=130cм h=hef+tf+tfˈ+t0=130+2+2+1=135
Решение Расчетное сопротивление бетона Rb = 17 МПа (умножается на 0,9)
Расчетное сопротивление арматур Rsc = 365 МПа (арматуру рекомендуют от 10 до 40 мм диаметром)
Определяем рабочую высоту балки ho = 560 мм
Находим требуемую площадь арматуры (Ао)
(по таблице №4 I =0,4;ƞ(I)=0,8)
Задаемся количеством стержней рабочей арматуры. При конструировании балки разрешено ставить стержни в один или два ряда по высоте каркаса =, при ширине балки более 200мм можно установить два или три каркаса в сечении, соответственно количество рабочих стержней может быть 2,3,..6 и т.д. d=22мм Количество=3 As=11,4 Из возможных вариантов армирования, оптимальным вариантом с точки зрения расходов является вариант с 3 стержнями.
Проверяем процент армирования
Определяем требуемую площадь сечения монтажных стержней
Определяем диаметр поперечных стержней
Определяем защитный слой бетона
Окончательно конструируем сечение элемента (стр.29)
Министерство сельского хозяйства Российской Федерации ФГБОУ ВО «Воронежский государственный аграрный университет имени императора Петра I» Факультет землеустройства и кадастров Кафедра мелиорации водоснабжения и геодезии
|
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 377; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.170.241 (0.013 с.) |


 Все теоремы и уравнения статистики выводится из нескольких исходных положений, принимаемых без математических доказательств называемых аксиомами или принципами статистики. Аксиомы статистики представляют собой результат обобщений многочисленных опытов и наблюдений над равновесием и движением тел, неоднократно подтвержденных практикой.
Все теоремы и уравнения статистики выводится из нескольких исходных положений, принимаемых без математических доказательств называемых аксиомами или принципами статистики. Аксиомы статистики представляют собой результат обобщений многочисленных опытов и наблюдений над равновесием и движением тел, неоднократно подтвержденных практикой. Вектор
Вектор  , равный диагонали параллелограмма, построенного на векторах
, равный диагонали параллелограмма, построенного на векторах  и
и  (рис.4), называется геометрической суммой векторов
(рис.4), называется геометрической суммой векторов  .
. .
. Такое равенство будет соблюдаться только при условии, что эти силы направлены по одной прямой в одну сторону. Если же векторы сил окажутся перпендикулярными, то
Такое равенство будет соблюдаться только при условии, что эти силы направлены по одной прямой в одну сторону. Если же векторы сил окажутся перпендикулярными, то 
 Следовательно, аксиому 3 можно еще формулировать так: две силы, приложенные к телу в одной точке, имеют равнодействующую, равную геометрической (векторной) сумме этих сил и приложенную в той же точке.
Следовательно, аксиому 3 можно еще формулировать так: две силы, приложенные к телу в одной точке, имеют равнодействующую, равную геометрической (векторной) сумме этих сил и приложенную в той же точке.
 Рис.7,а
Рис.7,а
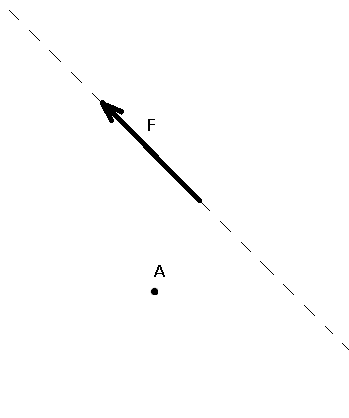 Рис.7,б
Рис.7,б
 Рис.7,в
Рис.7,в





 , так как ось z 2, относительно которой определялся статический момент площади, проходит через центр тяжести второй фигуры. В соответствии с основным своим свойством статический момент площади относительно любой центральной оси равен нулю. В связи с этим для сокращения арифметических вычислений при определении положения центра тяжести сложных фигур рекомендуется выбирать в качестве начала координат центр тяжести одной из простых фигур.
, так как ось z 2, относительно которой определялся статический момент площади, проходит через центр тяжести второй фигуры. В соответствии с основным своим свойством статический момент площади относительно любой центральной оси равен нулю. В связи с этим для сокращения арифметических вычислений при определении положения центра тяжести сложных фигур рекомендуется выбирать в качестве начала координат центр тяжести одной из простых фигур.
 100
100 


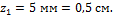












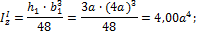
















 Элемент конструкции 1 (лист 100*16) присоединяется внахлестку к заведомо прочному элементу 2. Задана продольная сила N = 200 Кн, действующая на один элемент конструкции.
Элемент конструкции 1 (лист 100*16) присоединяется внахлестку к заведомо прочному элементу 2. Задана продольная сила N = 200 Кн, действующая на один элемент конструкции.