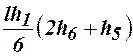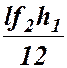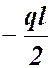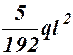Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Огинаючі епюри M і Q в нерозрізній балціСодержание книги
Поиск на нашем сайте
Огинаючими або обвідними епюрами вигинаючих моментів і поперечних силявляються епюри, в яких мають місце мінімальні і максимальні значення цих зусиль (Мmах, Мmіn, Q max, Q min) від одночасної дії на балку постійного та тимчасового навантаження. Для визначення максимального моменту Мmax в заданому перерізі балки до моменту від постійного навантаження Мпост. додають всі позитивні моменти від тимчасового навантаження Для визначення мінімального вигинаючого моменту Мmіп в будь-якому перерізі до моменту від постійного навантаження додають всі негативні моменти
Аналогічно визначають Q max та Q min:
Видно, що для побудови огинаючих епюр М і Q необхідно побудувати епюри вигинаючих моментів і поперечних сил методом фокусів при завантаженні нерозрізної балки постійним навантаженням. При дії тимчасового навантаження розглядають окремо кожен завантажений прольот і будують при цьому епюри Мтимч . і Q тимч .. На балці намічають ряд перерізів (кінці консолей, опори, середини прольотів, місця прикладання зосереджених сил або моментів) і для кожного перерізу по залежностях (2.24), (2.25), (2.26), (2.27) підраховують необхідні значення ординат обвідних епюр. Визначення ординат Мmax i Mmin зручно вести в табличній формі. Розглянемо ту ж нерозрізну балку (рис. 2.15а). За постійне навантаження приймемо рівномірно розподілене qпост. = 2 кН/м по всій довжині балки (рис. 2.20), а за тимчасове - те навантаження, яке діє на балку на рис. 2.15а. Методом фокусів будуємо епюру вигинаючих моментів від постійного навантаження qпост. = 2 кН/м по всій довжині балки. Епюра Мпост. показана на рис. 2.20б. По епюрі Мпост. побудуємо епюру Q пост .(рис. 2.20в). Завантажуємо прольот Завантажуємо прольот Завантажуємо праву консоль балки
Таблиця 2.8
Для побудови епюр вигинаючих моментів та поперечних сил можна частково використати дані з таблиці 2.3. Позначаємо на нерозрізній балці 8 перерізів (на опорах, в серединах прольотів, на консолі) (див.рис. 2.21а) і для кожного прийнятого перерізу за формулами (2.24)-(2.27) знаходимо максимальні та мінімальні значення вигинаючих моментів та поперечних сил. Підрахунки зручно вести в табличній формі (таблиці 2.8 і 2.9). По отриманих даних таблиці 2.9 в прийнятому масштабі будуємо огинаючу епюру моментів (рис. 2.21б). Для визначення
Таблиця 2.9
Рисунок 2.20
Рисунок 2.21
По даних таблиці 2.9 в прийнятому масштабі будуємо огинаючу епюру поперечних сил (рис. 2.21в) для заданої нерозрізної балки. Огинаючі епюри мають важливе значення при визначенні поперечних перерізів елементів конструкцій.
Розрахунково-графічна робота № 3 по темі “Розрахунок плоскої статично невизначУВАНОЇ рами методом переміщень” Розрахунок плоскої рами методом переміщень можна виконувати в канонічній чи розгорнутій формі. Необхідно: побудувати епюри згинаючих моментів М, поперечних Q та поздовжніх N сил, а також підібрати поперечні перерізи і перевірити на міцність. Розрахункові схеми плоских статично невизначених рам показані на рис. 3.1, вихідні дані приведені в таблиці 3.1.
Канонічна форма розрахунку 1. Встановлюють ступінь кінематичної невизначуваності рами за наступною формулою:
де
2. Вибирають основну систему методу переміщень, вводячи зв’язки, що перешкоджають можливим кутовим і лінійним переміщенням
Рисунок 3.1
3. Записують систему канонічних рівнянь методу переміщень для кінематично невизначуваної рами. Так, для три рази кінематично невизначуваної системи маємо наступну систему:
4. За даними додатку 4 будують одиничні епюри 5. Підраховують коефіцієнти та вільні члени системи канонічних рівнянь, розглядаючи рівновагу вузлів відповідних епюр або частин системи. Правильність підрахунку коефіцієнтів і вільних членів перевіряють так само як в методі сил. 6. Знайдені коефіцієнти і вільні члени підставляють в систему канонічних рівнянь і розв’язують її. 7. Будують виправлені одиничні епюри, помножаючи ординати одиничних епюр на знайдені значення невідомих 8. Будують остаточну розрахункову епюру згинаючих моментів Розрахунковий момент в будь-якому перерізі рами дорівнює:
9. За кінцевою епюрою згинаючих моментів будують епюру поперечних сил 10. Перевіряють правильність побудови епюри 11. Підбирають поперечні перерізи рами та перевіряють раму на міцність так само як при розрахунку рами методом сил. Таблиця 3.1 – Вихідні дані для РГР №3.
Примітка: погонна жорсткість визначається за формулою Рис. 3.7 – Варіанти розрахункових схем кінематично невизначуваних рам для РГР №3.
Продовження рис. 3.7
Розгорнута форма розрахунку 1. Так само, як і при канонічній формі розрахунку, визначають ступінь кінематичної невизначуваності заданої рамної конструкції. Див. формулу 3.1. 2. Записують основні та додаткові рівняння методу переміщень. Основні рівняння виражають умову рівності нулю суми моментів в кожному вільному жорсткому вузлі. Додаткові рівняння мають місце при наявності лінійних переміщень. Так, для рами, зображеній на рис. 3.1, основні рівняння мають вигляд:
Щоб скласти додаткове рівняння, відсікаємо частину рами так, щоб в переріз увійшли стержні, що мають лінійні переміщення, розглядаємо рівновагу відрізаної частини під дією заданого зовнішнього навантаження, прикладеного до відрізаної частини, і поперечних сил, прикладених до місць розрізу стержнів (рис. 3.2). Умовою рівноваги буде сума проекцій всіх сил на вісь, перпендикулярну до розрізаних стержнів, що дорівнює нулю.
Рисунок 3.2
3. За відомими залежностями (3.6) та (3.7) підраховують вузлові моменти, що входять до основних рівнянь, та поперечні сили, що входять до додаткових рівнянь: а) для стрижнів, жорстко закріпленого з обох боків:
а) для стрижнів, що має з одного боку шарнір:
Примітка: знак
Значення
4. Використовуючи основні та додаткові рівняння, формують систему рівнянь, в якій невідомими будуть кути повороту
5. Розв’язують систему рівнянь, знаходячи невідомі кути повороту
6. За приведеними залежностями для кожного стержня заданої рамної конструкції підраховують кінцеві згинаючі моменти і поперечні сили.
7. За підрахованими даними будують остаточні епюри згинаючих моментів
8. Перевіряють правильність побудованих епюр тими ж способами, що і при розрахунку рами методом сил.
9. Підбирають поперечні перерізи і перевіряють раму на міцність. Приклад розрахунку два рази кінематично невизначуваної плоскої рами методом переміщень (канонічна форма)
Необхідно: побудувати епюри згинаючих моментів М, поперечних Q та поздовжніх N сил, а також підібрати поперечні перерізи і перевірити на міцність. а) б) в) Рисунок 3.3 – а) Задана схема кінематично невизначуваної рами; б) шарнірна схема заданої рами; в) основна система. 1. Визначаємо ступінь кінематичної невизначуваності рами за формулою
2. Вибираємо основну систему 2 рази кінематично невизначуваної рами, вводячи зв’язки
3. Записуємо систему канонічних рівнянь для два рази кінематично невизначуваної рами:
4. За даними додатку 4 будуємо одиничні епюри
Рисунок 3.4 – Одиничні епюри
5. Підраховуємо коефіцієнти та вільні члени системи канонічних
6. Розв’язуємо систему рівнянь відносно невідомих
7. Будують виправлені епюри, помножуючи ординати одиничних епюр на відповідні значення невідомих
а) б) в) Рисунок 3.5 – Виправлені одиничні епюри 8. Будуємо остаточну епюру розрахункових моментів шляхом складання вантажної та сумарної епюр. Епюра показана на рис. 3.6 а. 9. Ділянка 12:
Ділянка 14:
а) б) в) Рисунок 3.6 – Остаточні епюри а) епюра згинаючих моментів, б) епюра поперечних сил та в) епюра поздовжніх зусиль.
Вузол 1:
12. Підбираємо поперечні перерізи рами у вигляді двотавра. Стрижень 1-2 (ригель): Стрижень 3-4 (ригель): За сортаментом підбираємо двотаври: Стрижень 1-2 (ригель): двотавр №12 ( Стрижень 3-4 (стійка): двотавр №10 (
Визначивши розміри, перевіряємо міцність стрижнів: Стрижень 1-2 (ригель):; Стрижень 3-4 (ригель): або
Отже, остаточно підібрані такі перерізи: стрижень 1-2 (ригель): двотавр № 12; стрижень 3-4 (стійка): двотавр № 10. Приклад розрахунку два рази кінематично невизначуваної плоскої рами методом переміщень (розгорнута форма) Необхідно: побудувати епюри згинаючих моментів М, поперечних Q та поздовжніх N сил, а також підібрати поперечні перерізи і перевірити на міцність. Схема рами зображена на рисунку 3.3 а.
1. Так само, як і при канонічній формі розрахунку, визначаємо ступінь кінематичної невизначеності. 2. Записуємо основне рівняння, виходячи з умови рівноваги жорсткого вузла 1.
Записуємо додаткове рівняння. Для цього перерізаємо стрижні, які мають лінійні зміщення. В нашому випадку це стрижні 1-3 та 1-4.
3. За відомими залежностями (3.6) та (3.7) підраховуємо вузлові моменти, що входять до основних рівнянь, та поперечні сили, що входять до додаткових рівнянь: Попередньо обрахуємо значення погонної жорсткості (формула 3.8):
4. Використовуючи основні та додаткові рівняння, формуємо систему рівнянь, в якій невідомими будуть кути повороту
Зазначимо, що система рівнянь, отримана при розгорнутій формі розрахунку, аналогічна системі рівнянь, отриманій при канонічній формі.
5. Розв’язуємо систему відносно
6. За приведеними залежностями для кожного стержня заданої рамної конструкції підраховуємо кінцеві згинаючі моменти і поперечні сили. 7.
7. За підрахованими даними будуємо остаточні епюри згинаючих моментів Розрахункові епюри зображені на рис. 3.6.
8. Наступні пункти аналогічні пунктам при розрахунку рами методом переміщень з використанням канонічної форми.
ДОДАТКИ Додаток 1
Додаток 2
Додаток 3
Додаток 4
Продовження дод. 4
Примітка: Повна таблиця для різних способів завантаження приведена в книзі Ю.И. Бурлакова и др. Строительная механика. – М., 1983. – с. 173. Додаток 5
Додаток 6
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 719; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.88.155 (0.01 с.) |

 в заданому перерізі.
в заданому перерізі.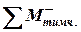 в заданому перерізі від тимчасового навантаження:
в заданому перерізі від тимчасового навантаження: , (2.24)
, (2.24) . (2.25)
. (2.25) , (2.26)
, (2.26) . (2.27)
. (2.27) тимчасовим навантаженням
тимчасовим навантаженням  кН і будуємо для балки епюри
кН і будуємо для балки епюри  та
та  (рис. 2.20г,д).
(рис. 2.20г,д). тимчасовим навантаженням
тимчасовим навантаженням 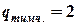 кН/м та будуємо епюри
кН/м та будуємо епюри  та
та  (рис. 2.20е,ж).
(рис. 2.20е,ж).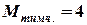 кНм і будуємо епюри
кНм і будуємо епюри  та
та  (рис. 2.20з,и).
(рис. 2.20з,и).



 та
та  таблицю 2.9 вигідно зробити в такому вигляді, щоб в місці прикладання зосередженої сили можна було б розглянути перерізи трохи лівіше та трохи правіше.
таблицю 2.9 вигідно зробити в такому вигляді, щоб в місці прикладання зосередженої сили можна було б розглянути перерізи трохи лівіше та трохи правіше.


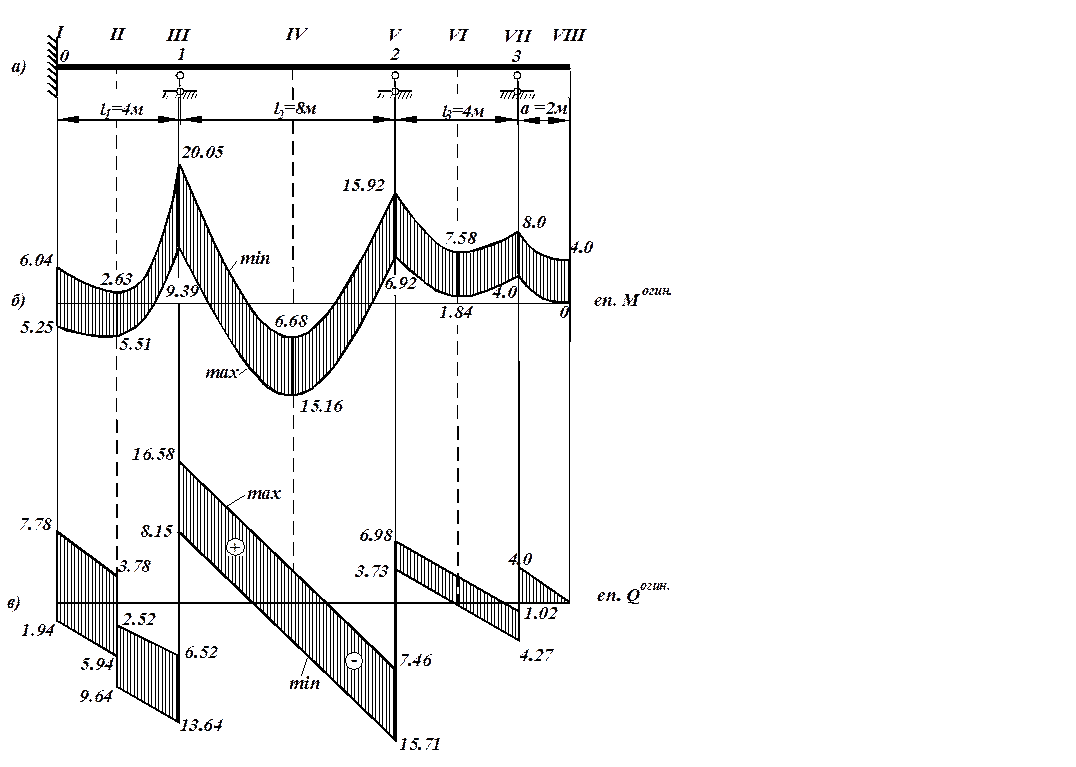
 (3.1)
(3.1) – кількість вільних рамних вузлів;
– кількість вільних рамних вузлів; – число можливих лінійних переміщень (підраховують для шарнірної розрахункової схеми рами, коли в кожний вузол заданої системи, включаючи й опорні, введені повні шарніри). Число можливих лінійних переміщень
– число можливих лінійних переміщень (підраховують для шарнірної розрахункової схеми рами, коли в кожний вузол заданої системи, включаючи й опорні, введені повні шарніри). Число можливих лінійних переміщень 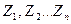 .
. Наприклад, для системи, зображеної на рис. 3.1 маємо:
Наприклад, для системи, зображеної на рис. 3.1 маємо:  (жорсткі вільні вузли 1 та 2),
(жорсткі вільні вузли 1 та 2),  (один додатковий стержень необхідно прикласти до шарнірної системи у вузлі 2, щоб перетворити її в геометрично незмінну).
(один додатковий стержень необхідно прикласти до шарнірної системи у вузлі 2, щоб перетворити її в геометрично незмінну). (3.2)
(3.2)
 ...,
...,  і вантажну
і вантажну  .
. ,
,  ,...,
,...,  , а також сумарну виправлену епюру
, а також сумарну виправлену епюру  .
.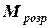 шляхом складання вантажної епюри
шляхом складання вантажної епюри  з сумарною виправленою
з сумарною виправленою  (3.3)
(3.3) , а за останньою – епюру поздовжніх сил
, а за останньою – епюру поздовжніх сил  .
. , м
, м
 , м
, м
 , кН
, кН
 , кН
, кН
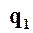 , кН/м
, кН/м
 , кН/м
, кН/м

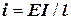 .
.

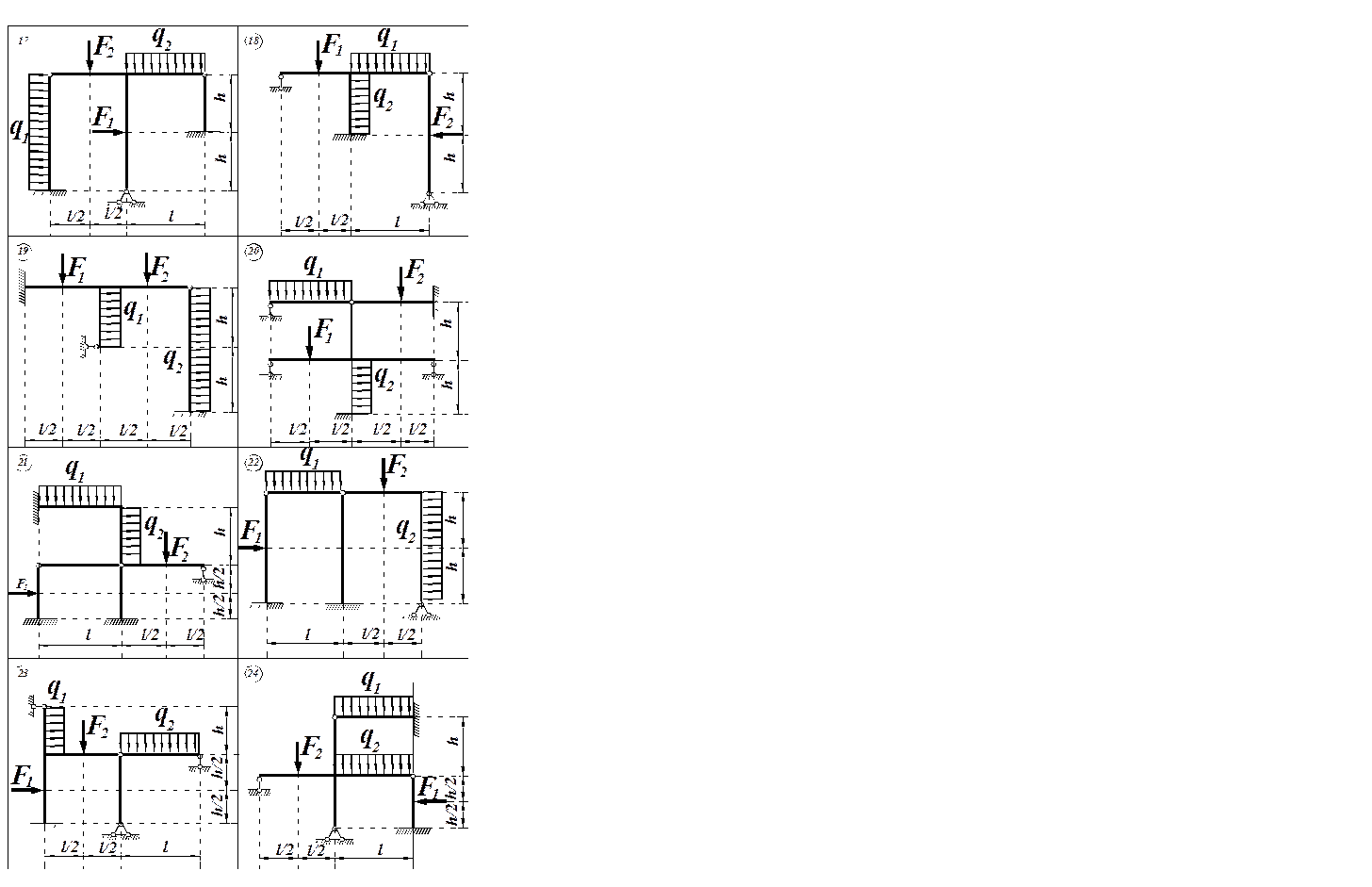

 (3.4)
(3.4) (3.5)
(3.5)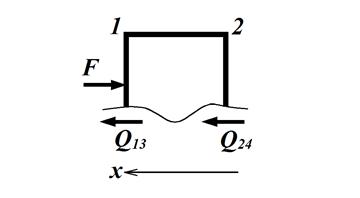
 (3.6)
(3.6) 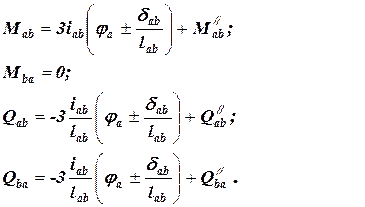 (3.7)
(3.7) (3.8)
(3.8) в формулах 3.6-3.7 вибирають за наступними схемами:
в формулах 3.6-3.7 вибирають за наступними схемами:

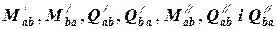 приймаємо за додатком 5.
приймаємо за додатком 5. та лінійні переміщення
та лінійні переміщення  та інші та лінійні переміщення
та інші та лінійні переміщення  і т.д.
і т.д. і поперечних сил
і поперечних сил 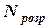 .
.
 , тобто система два рази кінематично невизначувана. В заданій рамі один жорсткий вузол, тобто
, тобто система два рази кінематично невизначувана. В заданій рамі один жорсткий вузол, тобто  . Кількість можливих лінійних переміщень визначаємо при дослідженні геометричної незмінності шарнірної схеми рами (рис. 3.3 б).
. Кількість можливих лінійних переміщень визначаємо при дослідженні геометричної незмінності шарнірної схеми рами (рис. 3.3 б).  та
та  . (рис. 3.3 в).
. (рис. 3.3 в).
 і вантажну
і вантажну 
 та
та  .
. рівнянь, розглядаючи рівновагу вузлів відповідних епюр або частин системи.
рівнянь, розглядаючи рівновагу вузлів відповідних епюр або частин системи. ;
;  ;
;  ;
;  ;
;  ;
;  .
.

 ,
,  , а також сумарну виправлену епюру
, а також сумарну виправлену епюру  ,
,  та сумарна виправлена епюра
та сумарна виправлена епюра  За остаточною епюрою моментів
За остаточною епюрою моментів  кН;
кН; кН;
кН; Ділянка 13:
Ділянка 13:  кН;
кН; кН
кН 11. Перевіряють правильність побудови епюри
11. Перевіряють правильність побудови епюри 
 ;
; ;
; ,
,  )
) ,
,  )
) , проте перенапруження складає 4,2 %, що знаходиться в межах інженерної точності розрахунків.
, проте перенапруження складає 4,2 %, що знаходиться в межах інженерної точності розрахунків.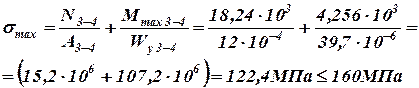 ;
;
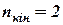 . Невідомими є кут повороту
. Невідомими є кут повороту  (
( ) та лінійне зміщення
) та лінійне зміщення  (
( - деформацією розтягу/стиску нехтуємо), тобто рама має дві невідомих. Для їх знаходження треба скласти два рівняння.
- деформацією розтягу/стиску нехтуємо), тобто рама має дві невідомих. Для їх знаходження треба скласти два рівняння.




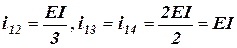 .
.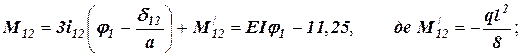



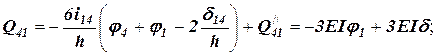

 - основне рівняння.
- основне рівняння.
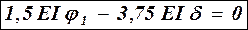 - додаткове рівняння.
- додаткове рівняння.




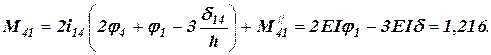


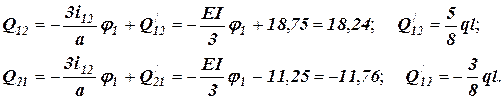
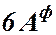





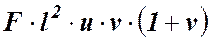





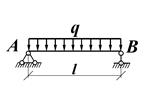


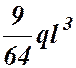

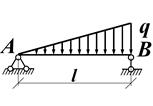








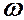

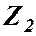



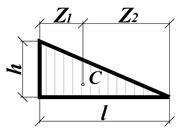


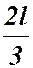

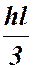











 Епюра
Епюра
 Епюра
Епюра