
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Загальні положення про розрахунок нерозрізних балокСодержание книги
Поиск на нашем сайте
Як і всі інші статично невизначувані системи нерозрізні балки розраховують або методом сил, або методом переміщень (деформацій). Відомий з курсу опору матеріалів також метод розрахунку за допомогою рівняння трьох моментів, який являє собою окремий випадок методу сил. Рівняння трьох моментів можуть бути виведені з канонічних рівнянь методу сил. З опору матеріалів уже відомо, що опори і, відповідно ним, опорні моменти, прийнято нумерувати зліва направо від нуля (на першій опорі) до n (на останній опорі). Прольотам нерозрізної балки присвоюють номер правої опори. Розглянемо нерозрізну балку, показану на рис.2.2а. Наведена балка три рази статично невизначувана. Основну систему можна вибрати двома способами: 1) відкинути проміжні (або будь-які інші) “зайві” опори. Замість них прикласти невідомі сили 2ф) розрізати балку над “зайвими” опорами і поставити в перерізах шарніри. При цьому, в обох випадках вибору основної системи (рис. 2.2в,д), невідомими будуть одиничні епюри вигинаючих моментів. Як видно, перший спосіб вибору основної системи дає нам право записати канонічні рівняння методу сил у вигляді:
Оскільки, коефіцієнти при невідомих в цій системі одержують шляхом перемноження відповідних одиничних епюр, то видно, що жоден із цих коефіцієнтів не буде дорівнювати нулю. Якщо ж збільшити число проміжних (“зайвих”) опор, тоді розрахунок ускладниться. Більш раціональним є другий спосіб вибору основної системи, а саме, розріз балки над опорами з постановкою в цих місцях шарнірів. Розглянемо частину нерозрізної балки (рис. 2.3а) з вибраною основною системою. Одиничні епюри для вибраної основної системи побудовані на рис.2.3б. Легко переконатися в тому, що при першому способі вибору основної системи одинична епюра деформує всю балку, а в другому випадку – кожний одиничний момент деформує лише два суміжні прольоти. Перше канонічне рівняння методу сил можна записати:
Вид n -го канонічного рівняння буде:
де
Якщо розглянути рис. 2.3б та залежність (2.4), то можна побачити, що для опори n не будуть нульовими переміщення
Рисунок 2.4
Тобто, кути розходження (повороту) на опорі n від одиничних моментів можна виразити:
Якщо отримані переміщення підставити в рівняння (2.5), прийнявши
Кожен член отриманого рівняння перемножимо на величину 6 Е та запишемо у вигляді рівняння:
Залежність (2.6) носить назву рівняння трьох моментів. Якщо прийняти жорсткість балки постійною, тоді матимемо:
Рисунок 2.5 Аналітичний розрахунок нерозрізної балки методом фокусів
Рисунок 2.6
Встановлено, що в незавантажених прольотах епюра вигинаючих моментів змінює знак. Зліва від завантаженого прольоту нульові точки на епюрі зміщені лівіше від середини прольоту, а справа – правіше від середини прольоту. Розташування цих нульових точок в незавантажених прольотах постійне і не залежить від інтенсивності та виду навантаження прольоту. Ці нульові точки називають моментними фокусами. Тобто мають місце ліві та праві моментні фокуси. Лівим (правим) моментним фокусом називається нульова точка епюри моментів даного прольоту при завантаженні одного або кількох прольотів, розташованих правіше (лівіше) від прольоту, який розглядається. Оскільки, фокусні точки в кожному прольоті мають постійне розташування, то і відношення опорних моментів незавантаженого прольоту теж буде постійним. Розрізняють ліві та праві моментні фокусні відношення. Лівим моментним фокусним відношенням для будь-якого прольоту є відношення правого опорного моменту до лівого опорного моменту, взяте з негативним знаком, коли зовнішнє навантаження знаходиться правіше цього прольоту. Ліве моментне фокусне відношення позначається
Ліве: Рисунок 2.7 Правим моментним фокусним відношенням для будь-якого прольоту є відношення лівого опорного моменту до правого опорного моменту, взяте з негативним знаком, коли зовнішнє навантаження знаходиться лівіше цього прольоту. Праве моментне фокусне відношення позначається Праве:
|
||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 367; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.152.146 (0.007 с.) |

 ,
,  ,
,  (рис. 2.2б,г);
(рис. 2.2б,г); ,
, , (2.3)
, (2.3) .
.
 . (2.4)
. (2.4) - кут розходження перерізів на опорі n від будь-якої одиничної сили;
- кут розходження перерізів на опорі n від будь-якої одиничної сили; - кутове переміщення в тому ж напрямку від
- кутове переміщення в тому ж напрямку від  ;
; - кут розходження перерізів на опорі n від
- кут розходження перерізів на опорі n від  ;
; - кут розходження перерізів на опорі n від
- кут розходження перерізів на опорі n від  .
. . Таким чином, із рівняння (2.4) маємо рівняння лише з трьома невідомими:
. Таким чином, із рівняння (2.4) маємо рівняння лише з трьома невідомими: . (2.5)
. (2.5) Рисунок 2.2
Рисунок 2.2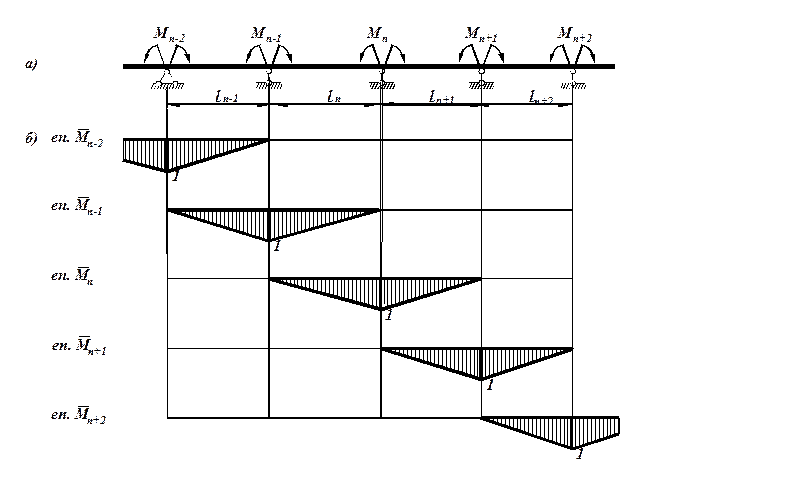 Рисунок 2.3
Рисунок 2.3 Для простої балки прольотом l, яка завантажена на опорі моментом (рис. 2.4), кути повороту будуть:
Для простої балки прольотом l, яка завантажена на опорі моментом (рис. 2.4), кути повороту будуть: ;
; 
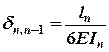 - кут повороту на опорі n від
- кут повороту на опорі n від  ;
; - кут повороту на опорі n від
- кут повороту на опорі n від  ;
; - кут повороту на опорі n від
- кут повороту на опорі n від  .
. . На опорі
. На опорі  , тоді:
, тоді: .
. , тоді отримаємо:
, тоді отримаємо: .
. . (2.6)
. (2.6) (2.7)
(2.7) Залежність (2.7) є рівнянням трьох моментів для балки постійної жорсткості. Нагадаємо ще залежності для визначення внутрішніх зусиль в перерізах нерозрізної балки (рис. 2.5):
Залежність (2.7) є рівнянням трьох моментів для балки постійної жорсткості. Нагадаємо ще залежності для визначення внутрішніх зусиль в перерізах нерозрізної балки (рис. 2.5): ;
;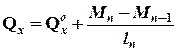 ;
; .
.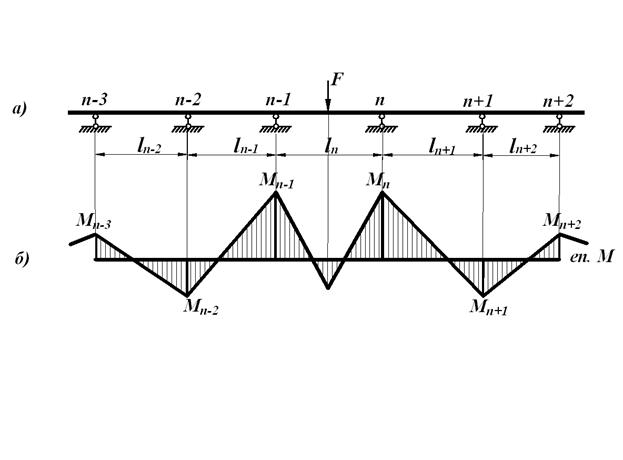 Метод моментних фокусів являє собою окремий випадок методу сил. Якщо в нерозрізній балці завантажений лише один прольот (рис. 2.6а), то епюра вигинаючих моментів має вигляд (рис. 2.6б):
Метод моментних фокусів являє собою окремий випадок методу сил. Якщо в нерозрізній балці завантажений лише один прольот (рис. 2.6а), то епюра вигинаючих моментів має вигляд (рис. 2.6б):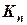 . Так для n -го прольоту (рис. 2.7) можна записати:
. Так для n -го прольоту (рис. 2.7) можна записати:
 .
.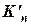 . Так для n -го прольоту (див. рис. 2.7) можна записати:
. Так для n -го прольоту (див. рис. 2.7) можна записати: .
.


